Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get all signed permutations of a list
ResourceFunction["SignedPermutations"][list] returns all the signed permutations of list. | |
ResourceFunction["SignedPermutations"][list,spec] returns signed permutations of type spec. |
All signed permutations of the list {1,2,3}:
| In[1]:= |
| Out[1]= | 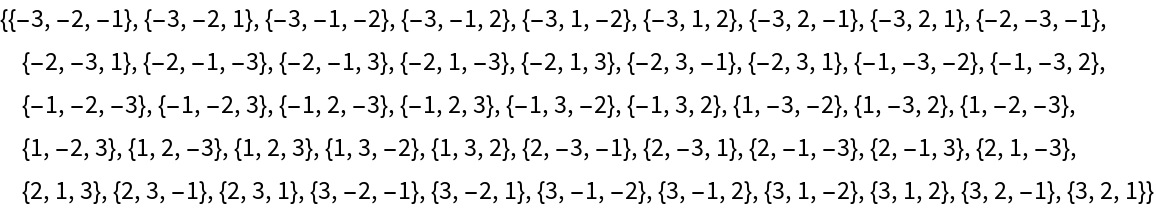 |
All signed even permutations of the list {1,2,3}:
| In[2]:= |
| Out[2]= | 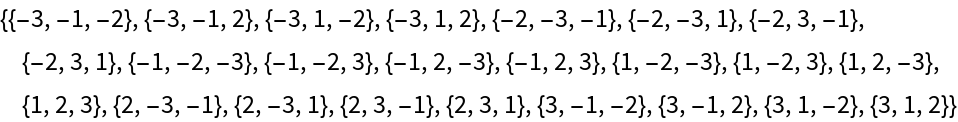 |
All signed cyclic permutations of the list {1,2,3}:
| In[3]:= |
| Out[3]= | 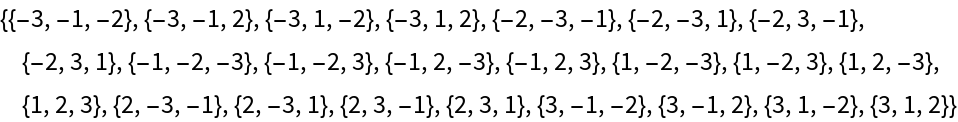 |
Find the vertices of a rhombic dodecahedron with edge lengths of ![]() :
:
| In[4]:= |
| Out[4]= |
Use ConvexHullMesh to generate the rhombic dodecahedron from its vertices:
| In[5]:= |
| Out[5]= | 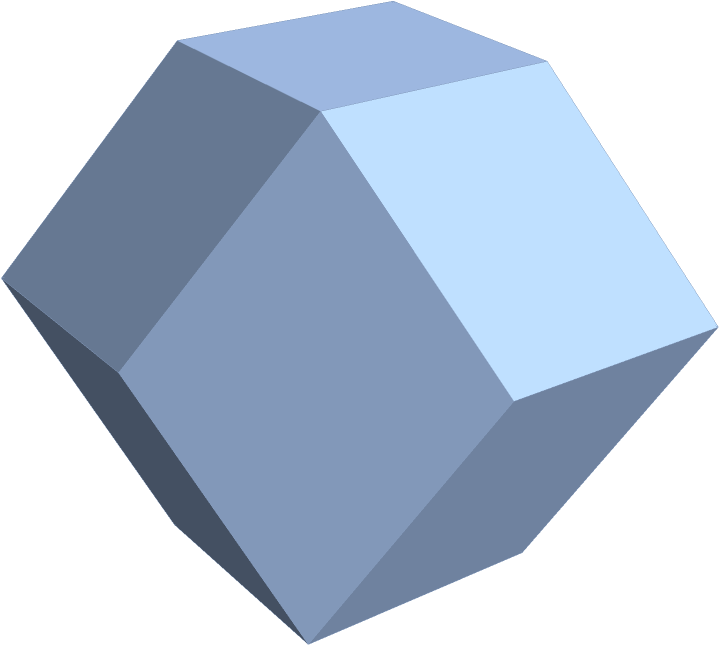 |
SignedPermutations[list,All] and SignedPermutations[list,"Symmetric"] are both equivalent to SignedPermutations[list]:
| In[6]:= | ![With[{n = 4}, ResourceFunction["SignedPermutations"][Range[0, n]] === ResourceFunction["SignedPermutations"][Range[0, n], All] === ResourceFunction["SignedPermutations"][Range[0, n], "Symmetric"]]](https://www.wolframcloud.com/obj/resourcesystem/images/19c/19c988e5-7cc1-42ba-9afd-2fcee2d02c32/5a8703b467863289.png) |
| Out[6]= |
Count all signed permutations corresponding to a given list, and compare with the expressions for the explicit counts:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
Create the 120 unit icosians that make the vertices of the 600-cell:
| In[14]:= | ![\[Phi] = RootReduce[GoldenRatio]; vecs = Join @@ (ResourceFunction["SignedPermutations"][#, "Even"] & /@ {{2, 0, 0, 0}, {1, 1, 1, 1}, {0, 1, \[Phi]^-1, \[Phi]}}/2);
icosians = ResourceFunction["Quaternion"] @@ # & /@ RootReduce[vecs];
RandomSample[icosians, 8]](https://www.wolframcloud.com/obj/resourcesystem/images/19c/19c988e5-7cc1-42ba-9afd-2fcee2d02c32/3276cab6eb6d2e7f.png) |
| Out[15]= | 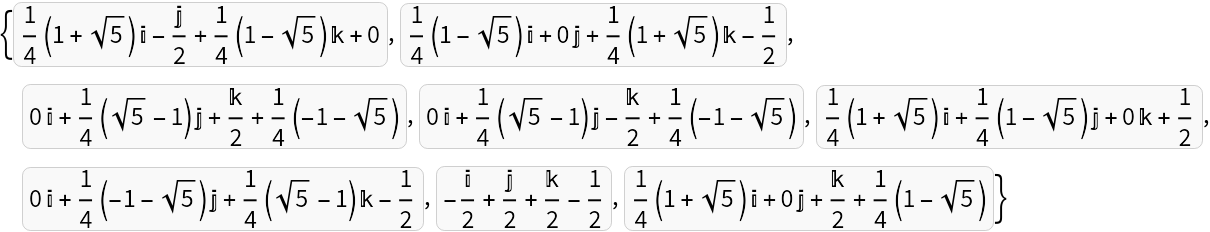 |
The icosians are a closed group under NonCommutativeMultiply (**), but RootReduce was needed for predictable results:
| In[16]:= | ![product = FunctionRepository`$09b0107d3e974bbf9deb28994f5b02d1`Quaternion[
Rational[-1, 2],
Rational[-1, 2],
Rational[1, 2],
Rational[1, 2]] ** FunctionRepository`$09b0107d3e974bbf9deb28994f5b02d1`Quaternion[
Rational[1, 2], Rational[1, 4] (1 + 5^Rational[1, 2]), Rational[1, 4] (1 - 5^Rational[1, 2]), 0];
Position[icosians, product]](https://www.wolframcloud.com/obj/resourcesystem/images/19c/19c988e5-7cc1-42ba-9afd-2fcee2d02c32/1b65cd897d60b817.png) |
| Out[17]= |
Create vertex sets for all 5 Platonic solids and 13 Archimedean solids with unit edges:
| In[18]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7fc481e1-85ec-4d2c-b951-638205f64926"]](https://www.wolframcloud.com/obj/resourcesystem/images/19c/19c988e5-7cc1-42ba-9afd-2fcee2d02c32/623620b1f53fc8bc.png) |
Show these sets with a half-unit sphere around each vertex:
| In[19]:= |
| Out[19]= | 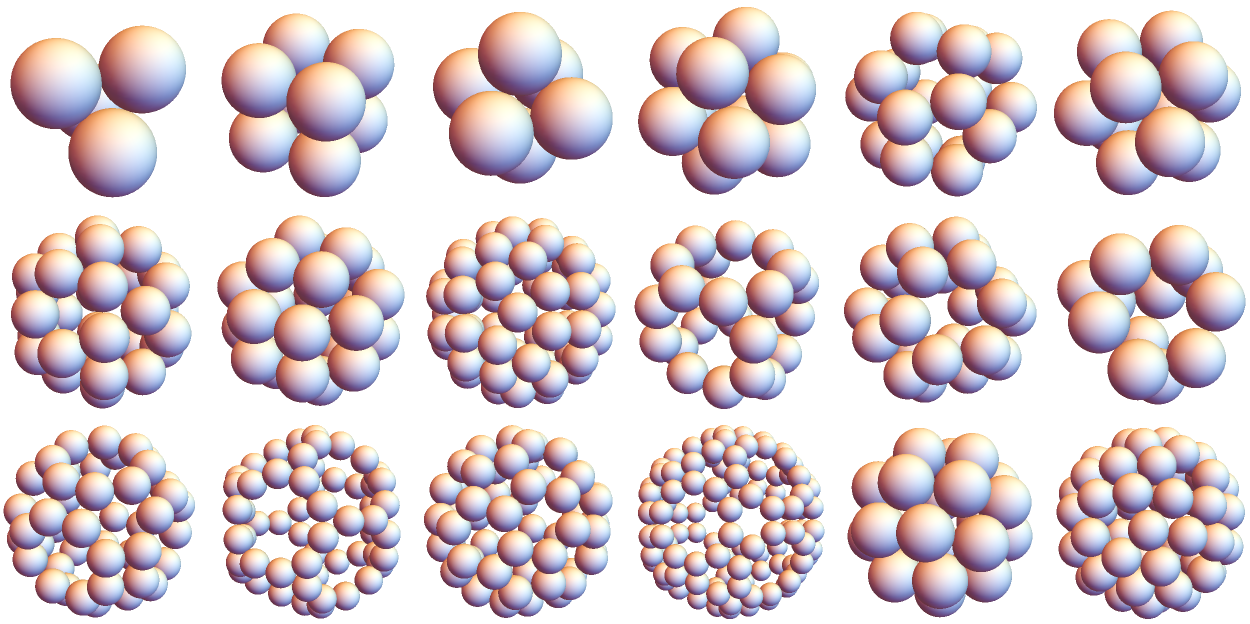 |
Show the polyhedra:
| In[20]:= |
| Out[20]= | 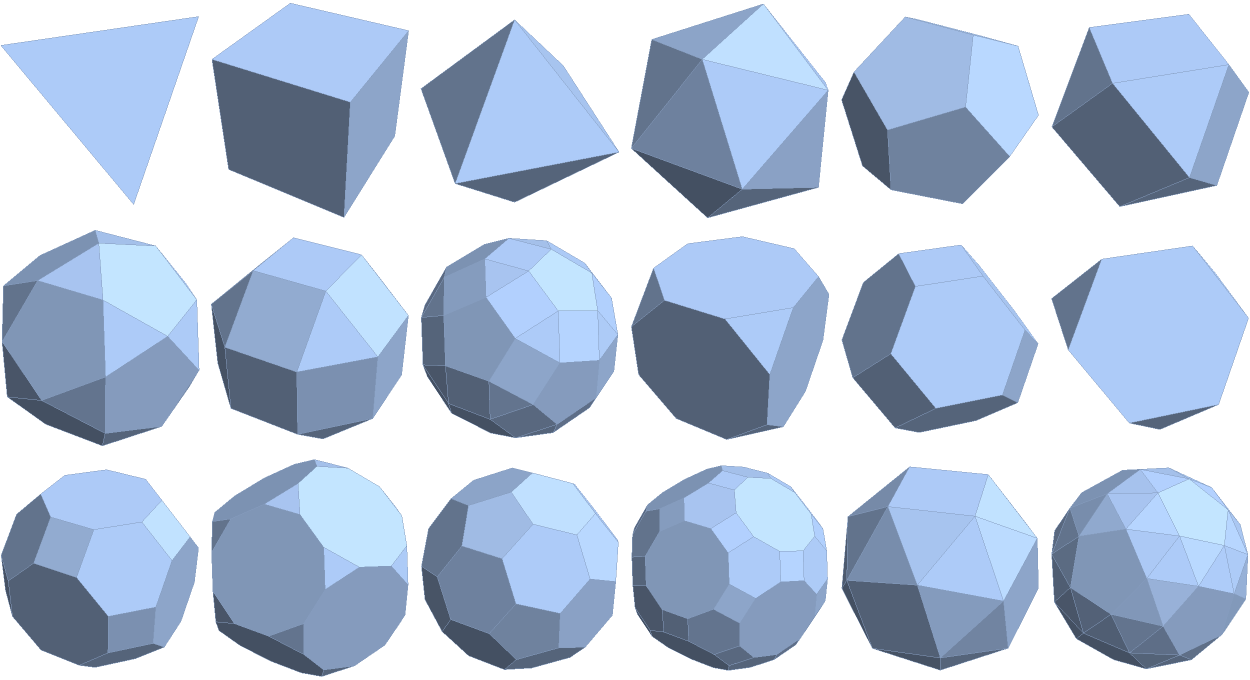 |
This work is licensed under a Creative Commons Attribution 4.0 International License