Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the confidence level corresponding to width around the mean of a normal distribution
ResourceFunction["SigmaConfidenceLevel"][σ] calculates the fraction of the normal distribution that falls within σ standard deviations of the mean. |
Calculate the confidence level at one standard deviation:
| In[1]:= |
| Out[1]= |
Calculate the p-value associated with 3σ:
| In[2]:= |
| Out[2]= |
SigmaConfidenceLevel returns exact outputs for exact inputs:
| In[3]:= |
| Out[3]= |
SigmaConfidenceLevel automatically threads over lists:
| In[4]:= |
| Out[4]= |
In physics, a discovery typically has to pass a five-σ of certainty test. Calculate the probability that a five-σ result is not a statistical fluctuation:
| In[5]:= |
| Out[5]= |
A p<0.05 test corresponds to a maximum displacement from mean of about 1.64 standard deviations:
| In[6]:= |
| Out[6]= |
SigmaConfidenceLevel can be defined as the integral between -σ and σ of the NormalDistribution with mean 0 and standard deviation 1:
| In[7]:= |
| Out[7]= |
Fit the mean prediction bands of a linear model fit with a confidence level of 1σ, 2σ and 3σ:
| In[8]:= | ![data = {{0, 1}, {1, 2}, {2, 3}, {3, 4}, {4, 4}};
fit = LinearModelFit[data, x, x];
Show[{
Plot[Evaluate[
fit["MeanPredictionBands", ConfidenceLevel -> ResourceFunction["SigmaConfidenceLevel"][N[#]]] & /@ Range[3]],
{x, -1, 5},
PlotStyle -> (GrayLevel /@ {0.0, 0.0, 0.4, 0.4, 0.8, 0.8}),
Filling -> {1 -> {2}, 3 -> {4}, 5 -> {6}}
],
ListPlot[data]
}]](https://www.wolframcloud.com/obj/resourcesystem/images/6ff/6ff3e113-b1d6-461c-a0ee-ee5b1c43fe54/0ed1e48481a3274e.png) |
| Out[10]= | 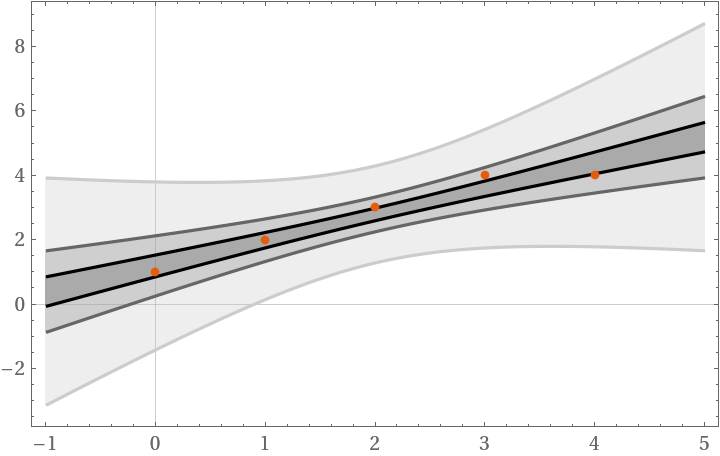 |
SigmaConfidenceLevel handles infinities:
| In[11]:= |
| Out[11]= |
The 5σ classification limit in physics for discoveries has a false-positive probability of approximately:
| In[12]:= |
| Out[12]= |
This work is licensed under a Creative Commons Attribution 4.0 International License