Function Repository Resource:

ShortInputForm

Explore the low-level structure of Wolfram Language expressions with an easy-to-read concise representation

Contributed by: Alexey Popkov

ResourceFunction["ShortInputForm"][expr]

produces terse version of expr intended for inspecting its low-level structure.

Details

ResourceFunction["ShortInputForm"] is intended for use within the Notebook interface.

ResourceFunction["ShortInputForm"][expr] produces a two-dimensional representation of expr, which may be immediately used as input.

Compound-type atomic objects like Image, Graph or NumericArray are kept untouched when they are present as a part of the supplied expression. Such objects can be converted into the corresponding input expressions by applying ResourceFunction["ShortInputForm"] to them directly.

ResourceFunction["ShortInputForm"][expr, Unevaluated] converts most compound-type atomic objects in expr into shortened input expressions. Compact low-level data representations like NumericArray and ByteArray are still kept untouched. They can also be converted by applying ResourceFunction["ShortInputForm"] to them directly.

For Graphics and Graphics3D objects, ResourceFunction["ShortInputForm"] removes duplicate options and sorts the options list.

Examples

Basic Examples (2)

Display the structure of a Graph expression's input form:

In[1]:=

Out[1]=

Explore the low-level structure of a graphics object produced by Plot. Try selecting subexpressions with the mouse, navigating with keyboard shortcuts, copying and editing code:

In[2]:=

Out[2]=

Copy a subexpression from above and use it in Graphics:

In[3]:=

Out[3]=

Applications (2)

Compare the internal structure of similar objects generated in different ways:

In[4]:=

${ListPlot3D[Table[Sin[x + y^2], {y, -2, 2, 1}, {x, -3, 3, 1}], Mesh -> None, Axes -> False, Boxed -> False], Plot3D[Sin[x + y^2], {x, -3, 3}, {y, -2, 2}, Mesh -> None, Axes -> False, Boxed -> False, PlotPoints -> {7, 5}, MaxRecursion -> 0]}$

Out[4]=

In[5]:=

Out[5]=

Check the result of applying Normal to a graphics object:

In[6]:=

pl = PointValuePlot[Table[RandomReal[10, 2] -> RandomReal[], 5], ColorFunction -> "Rainbow"];
plNormalized = Normal@pl;
ResourceFunction["ShortInputForm"]@pl

Out[8]=

In[9]:=

Out[9]=

Properties and Relations (4)

InputForm always produces a one-dimensional representation of the expression in the form of pure text, suitable to be typed as Wolfram Language input via text-based interface. Within the notebook interface, semantic selection and code highlighting aren't available with InputForm expressions:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

ShortInputForm produces shortened two-dimensional output, suitable to be used as input within the notebook interface. Semantic selection and code highlighting are turned on by default:

In[12]:=

Out[12]=

Special forms like NumericArray by default are kept untouched for readability, but can also be converted by applying ShortInputForm to them separately:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

Such forms usually can be converted to normal expressions by applying Normal:

In[15]:=

Out[15]=

Possible Issues (3)

By default ShortInputForm[expr] keeps untouched compound-type atomic objects when they are part of the supplied expression:

In[16]:=

$expr = {RandomImage[1, {50, 40, 20}], DelaunayMesh[RandomReal[1, {7, 3}]], Graph[{1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1}], SparseArray[{{5}} -> 1, {6}], NumericArray[RandomReal[1, {5, 5}], "Real64"]}; AtomQ /@ expr$

Out[17]=

In[18]:=

Out[18]=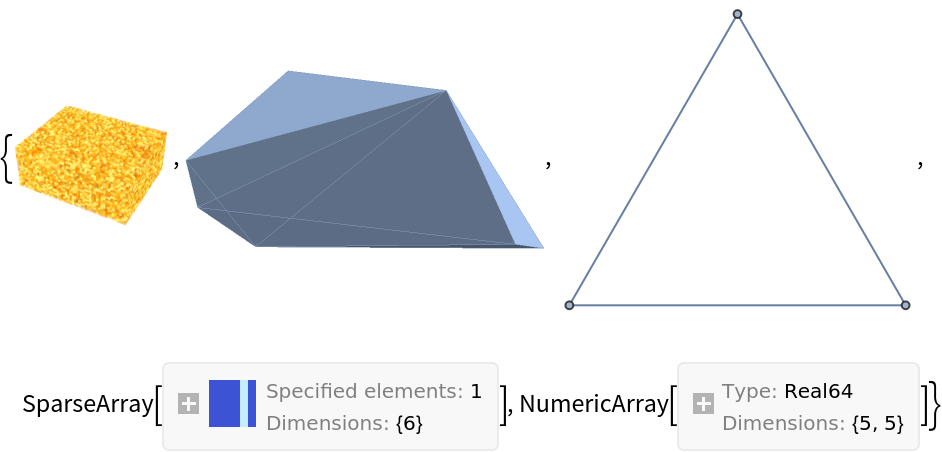

Use ShortInputForm[expr, Unevaluated] to convert most of them into actual input expressions revealing their low-level structure:

In[19]:=

Out[19]=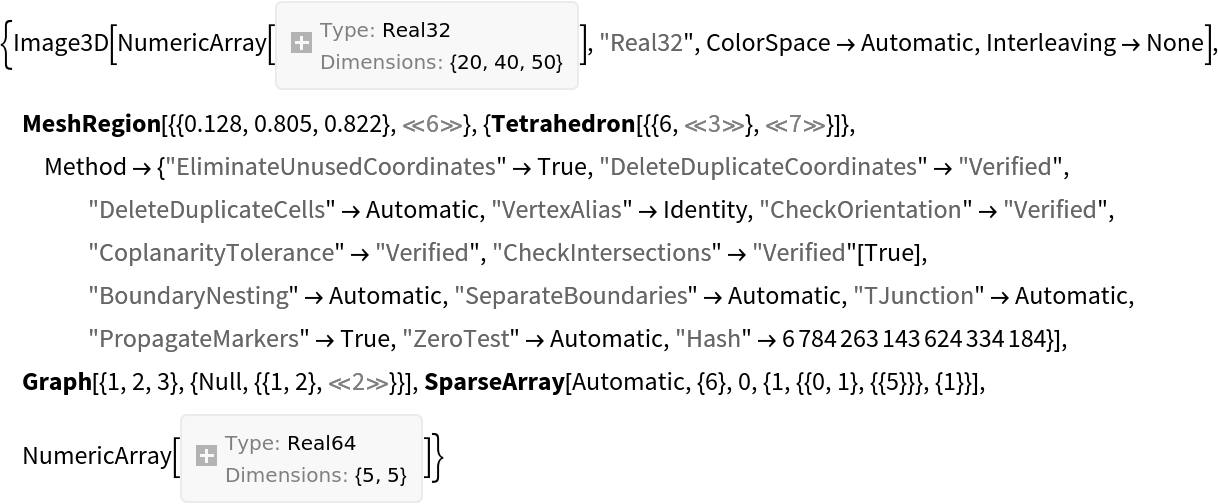

Alternatively, apply ShortInputForm to the atomic objects directly:

In[20]:=

Out[20]=

Neat Examples (3)

Box structure inspection (1)

Explore box structures generated by ToBoxes taking advantage of the easy-to-read representation generated by ShortInputForm:

In[21]:=

$Graph[{1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1}] // ToBoxes // ResourceFunction[ "ShortInputForm"]$

Out[21]=

PDF formatting (2)

Create an auxiliary function that exports a supplied expression to "PDF" and then immediately imports the results as vector graphics:

In[22]:=

$vectorExportImportPDF[expr_] := First@ImportString[ ExportString[expr, "PDF", "AllowRasterization" -> False], If[$VersionNumber >= 12.2, {"PDF", "PageGraphics"}, {"PDF", "Pages"}], "TextOutlines" -> False]; graphics2D = Plot[Sin[x], {x, 0, 10}, Axes -> False]$

Out[22]=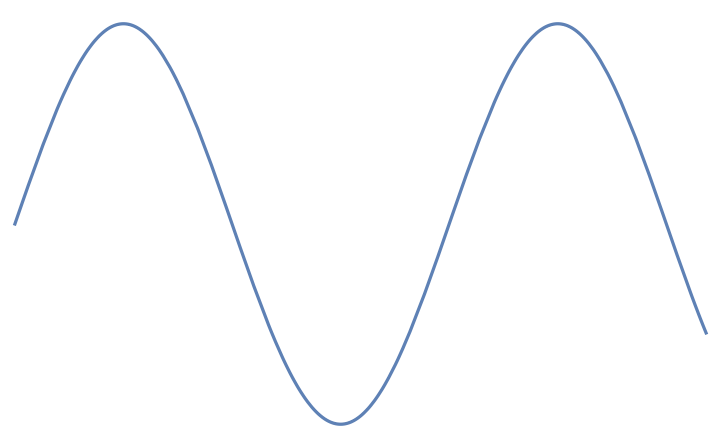

Inspect the internal contents of returned graphics with ShortInputForm:

In[23]:=

Out[24]=

In[25]:=

Out[25]=

Publisher

AlexeyPopkov

Version History

1.1.1 – 20 September 2022
1.1.0 – 15 February 2022
1.0.0 – 11 January 2022

Source Metadata

Citation:
- Alexey Popkov, "shortInputForm. Shortened and formatted InputForm for Wolfram Mathematica." // GitHub (2022) [Electronic resource.] – URL: https://github.com/AlexeyPopkov/shortInputForm.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

ShortInputForm

Details