Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SequenceLimit

Source Notebook

Numerically estimate the limit of a sequence of values

Contributed by: Jan Mangaldan

ResourceFunction["SequenceLimit"][{n1,n2,…}]

estimates the limit of the numerical sequence ni.

Details and Options

ResourceFunction["SequenceLimit"] uses different sequence transformation algorithms for finding the numerical limit of a sequence.
Depending on the value of the option Method, the following implementions can be chosen:
"WynnEpsilon"top-level implementation of the Wynn epsilon algorithm
"NSequenceLimit"built-in implementation of the Wynn epsilon algorithm from NumericalMath`
"BrezinskiTheta"Brezinski's theta algorithm
"Euler"Euler transformation
Automaticchooses the method depending on the precision and length of the sequence
ResourceFunction["SequenceLimit"][list,Method→{"NSequenceLimit","Degree"→1}] uses Aitken's delta-squared algorithm.
ResourceFunction["SequenceLimit"][list,Method→{"NSequenceLimit","Degree"→n}] specifies the degree of the transformation to be used by SequenceLimit.
In general, there must be at least 2n+2 terms in list for a degree-n transformation.
ResourceFunction["SequenceLimit"][list,Method→{"WynnEpsilon","Parameter"→h}] applies a generalization of the Wynn epsilon algorithm due to Vanden-Broeck and Schwartz, with adjustable parameter h.
h⩵1 corresponds to the classical Wynn epsilon algorithm, while h⩵0 corresponds to the iterated Aitken delta-squared process.
ResourceFunction["SequenceLimit"][list,Method→{"Euler","EulerRatio"→q}] applies Wynn's implementation of the Euler-Knopp transform. q is the fixed ratio used in the transformation.

Examples

Basic Examples (3) 

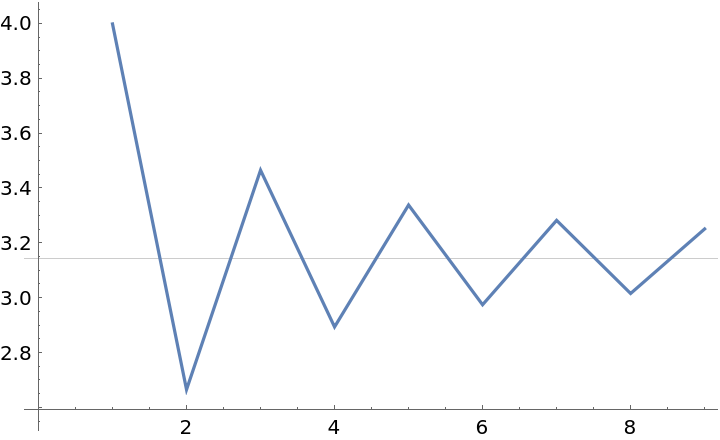
Build a sequence approximating Pi:

In[1]:=
seq = Accumulate[4 Table[(-1)^k/(2 k + 1), {k, 0, 8}]]
Out[1]=
In[2]:=
ListPlot[seq, Joined -> True, GridLines -> {{}, {Pi}}]
Out[2]=

Find an approximation of the limit of the sequence:

In[3]:=
limit = ResourceFunction["SequenceLimit"][seq]
Out[3]=

The approximation is much closer to the limit than the last term of the sequence:

In[4]:=
Pi - N[{limit, Last[seq]}]
Out[4]=

Scope (3) 

Symbolic sequences:

In[5]:=
ResourceFunction["SequenceLimit"][{a, b, c}] // Simplify
Out[5]=

Rational sequences:

In[6]:=
seq = Table[(1 + 1/n)^n, {n, 8}]
Out[6]=
In[7]:=
ResourceFunction["SequenceLimit"][seq]
Out[7]=
In[8]:=
E - N[%]
Out[8]=

Real-valued sequences:

In[9]:=
ResourceFunction["SequenceLimit"][N[Table[1 + 1/i^2, {i, 10}]]]
Out[9]=

Complex-valued sequences:

In[10]:=
ResourceFunction["SequenceLimit"][Accumulate[N[Table[I^k/k, {k, 10}]]]]
Out[10]=
In[11]:=
-Log[1 - I] - %
Out[11]=

Options (19) 

Method (19) 

WynnEpsilon (6) 

Use the top-level implementation of the Wynn epsilon method:

In[12]:=
ResourceFunction["SequenceLimit"][1./Range[10]^2, Method -> "WynnEpsilon"]
Out[12]=

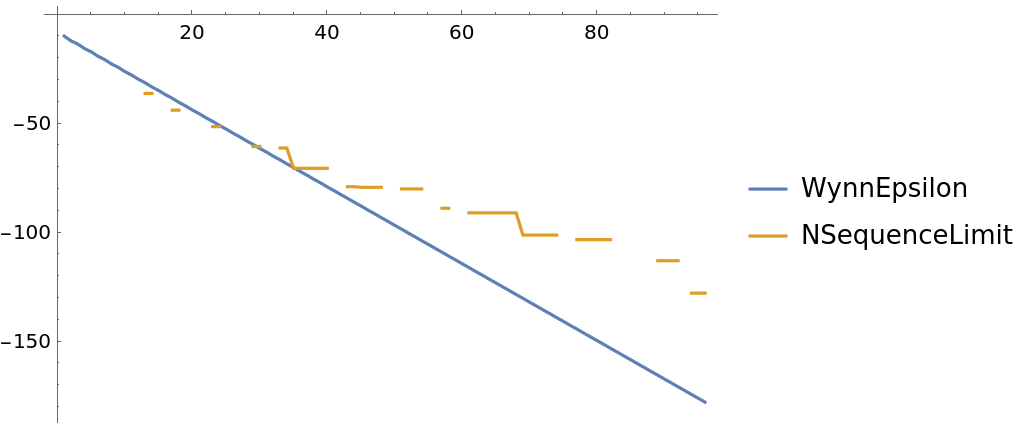
The top-level "WynnEpsilon" method can be more accurate:

In[13]:=
pi4[n_] := N[Accumulate[Table[(-1)^k/(2 k + 1), {k, 0, n}]], 100]
In[14]:=
methods = {"WynnEpsilon", "NSequenceLimit"};
In[15]:=
ListPlot[ Table[Log@ Abs[Pi/4 - Table[ResourceFunction["SequenceLimit"][pi4[n], Method -> method], {n, 5, 100}]], {method, methods}], Joined -> True, PlotLegends -> methods]
Out[15]=

Generate partial sums of the Basel series:

In[16]:=
seq = Accumulate[N[1/Range[11]^2, 20]]
Out[16]=

With the default settings, "WynnEpsilon" does not give a good result:

In[17]:=
r1 = ResourceFunction["SequenceLimit"][seq, Method -> "WynnEpsilon"]
Out[17]=

Adjust the parameter of the transformation to give a better result:

In[18]:=
r2 = ResourceFunction["SequenceLimit"][seq, Method -> {"WynnEpsilon", "Parameter" -> -1}]
Out[18]=
In[19]:=
\[Pi]^2/6 - {r1, r2}
Out[19]=

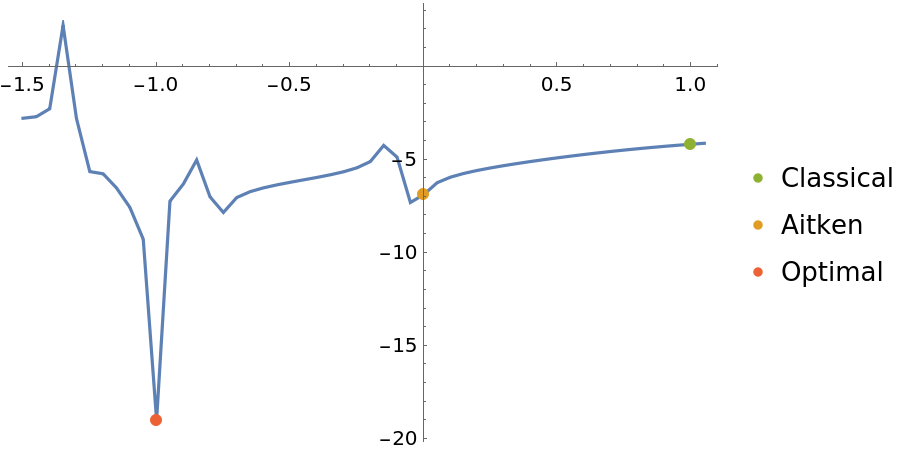
Plot the relative accuracy of the transformation for various values of the parameter:

In[20]:=
Legended[ ListLinePlot[ Table[{p, Log[Abs[ResourceFunction["SequenceLimit"][seq, Method -> {"WynnEpsilon", "Parameter" -> p}] - \[Pi]^2/ 6]/(\[Pi]^2/6)]}, {p, -1.5, 1.05, 0.05}], Mesh -> {{{1, Directive[ColorData[97, 3], AbsolutePointSize[6]]}, {0, Directive[ColorData[97, 2], AbsolutePointSize[6]]}, {-1, Directive[ColorData[97, 4], AbsolutePointSize[6]]}}}, PlotRange -> All], PointLegend[{ColorData[97, 3], ColorData[97, 2], ColorData[97, 4]}, {"Classical", "Aitken", "Optimal"}]]
Out[20]=
NSequenceLimit (4) 

Use the built-in implementation of the Wynn epsilon method:

In[21]:=
ResourceFunction["SequenceLimit"][1. + 1/Range[8]^2, Method -> "NSequenceLimit"]
Out[21]=

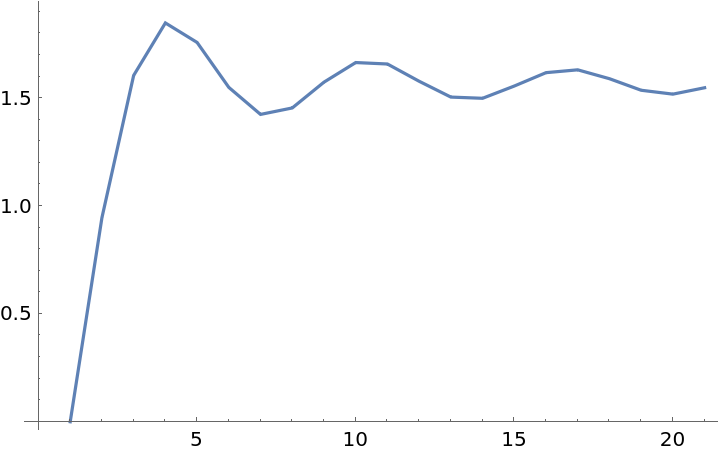
Find approximations of the limit of a sequence using different Wynn degrees:

In[22]:=
seq = Table[SinIntegral[x], {x, 0, 20}] // N;
In[23]:=
ListPlot[seq, Joined -> True]
Out[23]=
In[24]:=
ResourceFunction["SequenceLimit"][seq, Method -> {"NSequenceLimit", "Degree" -> #}] & /@ Range[8]
Out[24]=

Compare the errors:

In[25]:=
% - Pi/2
Out[25]=
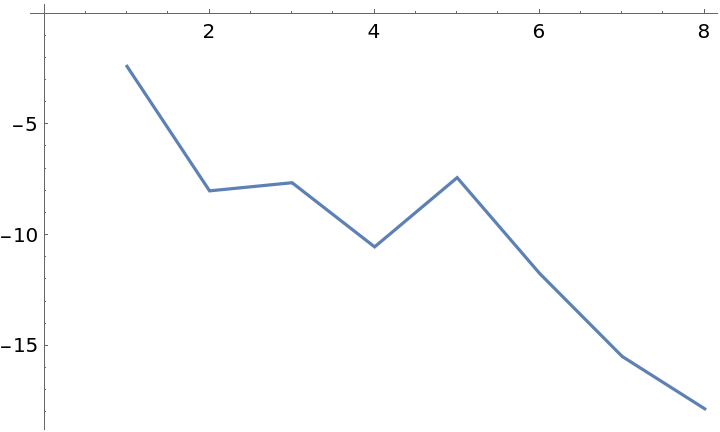
In[26]:=
ListPlot[Log[Abs[%]], Joined -> True]
Out[26]=

The built-in "NSequenceLimit" method can be faster than the top-level implementation:

In[27]:=
seq = Accumulate[Table[(-1)^k/(2 k + 1), {k, 0, 20}]] // N;
In[28]:=
RepeatedTiming[ Pi/4 - ResourceFunction["SequenceLimit"][seq, Method -> #]] & /@ {"WynnEpsilon", "NSequenceLimit"}
Out[28]=
BrezinskiTheta (3) 

Partial sums of the :

In[29]:=
seq = Accumulate[Table[(-1)^k/(k + 1), {k, 0, 12}]] // N
Out[29]=

Apply Brezinski's ϑ-algorithm to accelerate the convergence:

In[30]:=
r0 = ResourceFunction["SequenceLimit"][seq, Method -> "BrezinskiTheta"]
Out[30]=

Compare with the exact result:

In[31]:=
Log[2] - %
Out[31]=
Euler (6) 

Partial sums of a Dirichlet series:

In[32]:=
seq = Accumulate[N[Table[(-1)^k (2 k + 3)^4, {k, 0, 6}]]]
Out[32]=

The Euler transformation gives better results than the default:

In[33]:=
r0 = ResourceFunction["SequenceLimit"][seq]
Out[33]=
In[34]:=
r1 = ResourceFunction["SequenceLimit"][seq, Method -> "Euler"]
Out[34]=
In[35]:=
With[{s = -4}, LerchPhi[-1, s, 3/2]/2^s] - {r0, r1}
Out[35]=

Partial sums of an alternating series:

In[36]:=
seq = Accumulate[N[Table[(-1/2)^k/(2 k + 1)^2, {k, 0, 16}]]]
Out[36]=

Apply the Euler transformation:

In[37]:=
r1 = ResourceFunction["SequenceLimit"][seq, Method -> "Euler"]
Out[37]=

Apply the Euler transformation with a different setting of the fixed ratio:

In[38]:=
r2 = ResourceFunction["SequenceLimit"][seq, Method -> {"Euler", "EulerRatio" -> -1/2}]
Out[38]=

Compare both results with the exact result:

In[39]:=
HurwitzLerchPhi[-1/2, 2, 1/2]/4 - {r1, r2}
Out[39]=

Properties and Relations (2) 

Applying SequenceLimit to the partial sums of a power series gives the same result as PadeApproximant:

In[40]:=
Clear[x]
In[41]:=
ps = Accumulate[Table[x^k/k!, {k, 0, 7}]]
Out[41]=
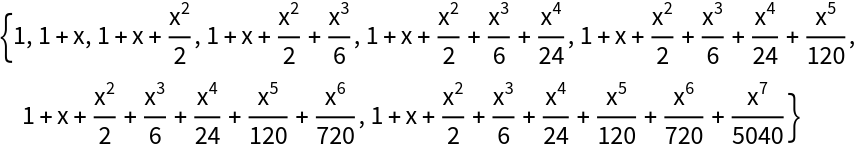
In[42]:=
Block[{rat = Simplify[ResourceFunction["SequenceLimit"][ps]], c}, c = Coefficient[Denominator[rat], x, 0]; (Expand[Numerator[rat]/c])/(Expand[Denominator[rat]/c])]
Out[42]=
In[43]:=
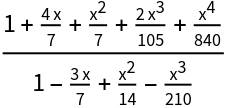
PadeApproximant[Exp[x], {x, 0, {4, 3}}]
Out[43]=

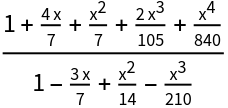
SequenceLimit can be used to compute limits, just like NLimit from NumericalCalculus`:

In[44]:=
Table[Sin[Exp[-x]]/Exp[-x], {x, 0, 5}] // N
Out[44]=
In[45]:=
ResourceFunction["SequenceLimit"][%]
Out[45]=
In[46]:=
Needs["NumericalCalculus`"]
In[47]:=
NLimit[Sin[x]/x, x -> 0]
Out[47]=

Possible Issues (3) 

SequenceLimit can encounter numerical errors:

In[48]:=
seq = {1, 11/20, 1/10, .001}
Out[48]=
In[49]:=
ResourceFunction["SequenceLimit"][seq]
Out[49]=

Sometimes the errors can be avoided by numerically disturbing the sequence or changing its precision:

In[50]:=
ResourceFunction["SequenceLimit"][seq + RandomReal[{-.0001, .0001}, 4]]
Out[50]=
In[51]:=
ResourceFunction["SequenceLimit"][N[seq]]
Out[51]=

SequenceLimit can give unexpected results for divergent sequences:

In[52]:=
seq = Accumulate[N[Table[(-1)^(k - 1) k!, {k, 0, 24}], 20]]
Out[52]=
In[53]:=
ResourceFunction["SequenceLimit"][seq]
Out[53]=
In[54]:=
N[E ExpIntegralEi[-1]]
Out[54]=

Version History

  • 2.1.0 – 22 December 2020
  • 2.0.0 – 09 April 2020
  • 1.0.0 – 03 April 2020

Source Metadata

  • Citation:
    • Brezinski C., Accélération de suites a convergence logarithmique, Comptes Rendus de l’Académie des Sciences Série A, vol. 273, 727–730, 1971
      Available online https://gallica.bnf.fr/ark:/12148/bpt6k56191671/f41.item
    • Broeck J.-M.V., Schwartz L.W., A One-Parameter Family of Sequence Transformations, SIAM Journal on Mathematical Analysis, vol. 10, no. 3, 658–666, 1979
      DOI: 10.1137/0510061
    • Weniger E.J., Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series, Computer Physics Reports, vol. 10, no. 5–6, 189–371, 1989
      DOI: 10.1016/0167-7977(89)90011-7
      Available online https://arxiv.org/abs/math/0306302
    • Wynn P., A note on the generalised Euler transformation, The Computer Journal, vol. 14, no. 4, 437–441, 1971
      DOI: 10.1093/comjnl/14.4.437

Related Resources

Author Notes

The top-level implementation of the “WynnEpsilon” method is adapted from https://tpfto.wordpress.com/2019/03/13/the-wynn-%ce%b5-algorithm-and-pade-approximation/.

License Information