Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate subsets that satisfy a certain criterion
ResourceFunction["SelectSubsets"][list,crit] gives a list of all possible subsets of list that satisfy the criterion crit. | |
ResourceFunction["SelectSubsets"][list,n,crit] gives all subsets containing at most n elements that satisfy crit. | |
ResourceFunction["SelectSubsets"][list,{n},crit] gives all subsets containing exactly n elements that satisfy crit. | |
ResourceFunction["SelectSubsets"][list,{nmin,nmax},crit] gives all subsets containing between nmin and nmax elements that satisfy crit. | |
ResourceFunction["SelectSubsets"][list,nspec,crit,s] limits the results to the first s subsets. |
Select subsets from {1,2,3,4,5} that add up to 10:
| In[1]:= |
| Out[1]= |
Select subsets of length 2 to 4 that sum up to a prime:
| In[2]:= |
| Out[2]= |
Select all subsets of length 2 that add up to 6:
| In[3]:= |
| Out[3]= |
Select all subsets that add up to 0:
| In[4]:= |
| Out[4]= |
Select all subsets of odd length that add up to a prime:
| In[5]:= |
| Out[5]= | 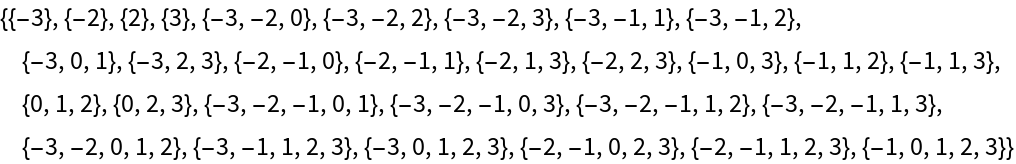 |
Select the first eight subsets that add up to a prime:
| In[6]:= |
| Out[6]= |
Find subsets that add up to 25:
| In[7]:= |
| Out[7]= |
The main difference between Select and Subsets, and SelectSubsets is the amount of memory used:
| In[8]:= |
| Out[8]= |
Compared to naive implementation, which requires roughly a 1000 times more memory:
| In[9]:= |
| Out[9]= |
Verify the result is the same:
| In[10]:= |
| Out[10]= |
With a criterion that is a tautology, SelectSubsets and Subsets give the same results:
| In[11]:= |
| Out[11]= |
SelectSubsets might not be able to return the number of elements that are requested:
| In[12]:= |
| Out[12]= |
Find subsets that add up to 0:
| In[13]:= |
| Out[14]= |
Visualize the lengths of the lists:
| In[15]:= |
| Out[15]= | 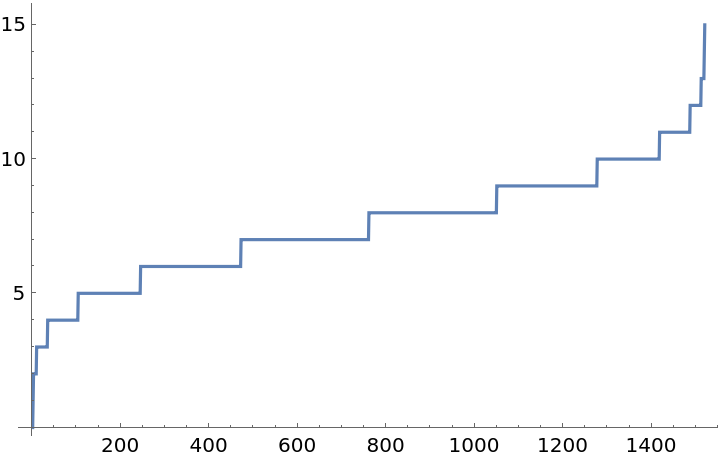 |
This work is licensed under a Creative Commons Attribution 4.0 International License