Basic Examples (2) 

Select from the list {5,6,7,8,9} those permutations that form a prime when concatenating the digits:

In[1]:=

Out[1]=

Select those permutations having length 3:

In[2]:=

Out[2]=

Select those permutations having length 3–4:

In[3]:=

Out[3]=

Select permutations of {1,2,3,4} for which the first two elements and the last elements add up to the same value:

In[4]:=

Out[4]=

Scope (1) 

Select the first 10 permutations of length 4 for which the elements add up to an odd number:

In[5]:=

Out[5]=

Applications (2) 

Select polynomials for which the slope is 1 at x=0:

In[6]:=

Out[6]=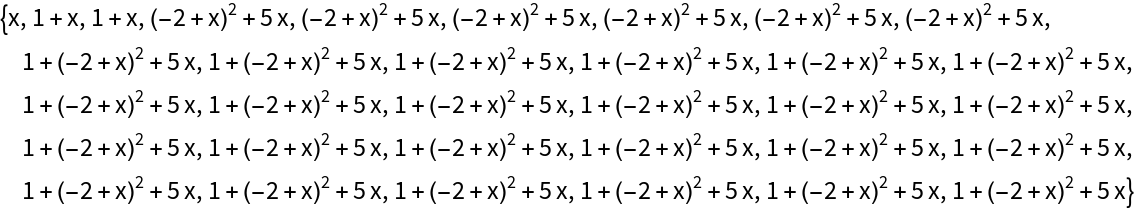

Confirm that the slope is indeed unity at x=0:

In[7]:=

Out[7]=

Properties and Relations (3) 

Duplicated items are treated the same:

In[8]:=

Out[8]=

The main difference between SelectPermutations[list,crit] and Select[Permutations[list],crit] is the memory usage:

In[9]:=

Out[9]=

Using Select and Permutations uses 500 times more memory:

In[10]:=

Out[10]=

Verify that the results are identical:

In[11]:=

Out[11]=

Head does not have to be List:

In[12]:=

Out[12]=

Possible Issues (2) 

SelectPermutations might take longer as it is written in higher-level code as compared to the implementation of Permutations:

In[13]:=

Out[14]=

Using the built-in functions is faster at the expense of 500× more memory:

In[15]:=

Out[16]=