Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine if two line segments intersect
ResourceFunction["SegmentIntersectionQ"][{a,b},{c,d}] determines if line segments | |
ResourceFunction["SegmentIntersectionQ"][{{a,b},{c,d}}] determines if line segments | |
Determine if two segments intersect:
| In[1]:= |
| Out[1]= |
Show a trapezoid:
| In[2]:= |
| Out[2]= |  |
Determine if diagonal segments of a trapezoid intersect:
| In[3]:= |
| Out[3]= |
Determine if the non-parallel segments of a trapezoid intersect:
| In[4]:= |
| Out[4]= |
Determine if neighboring segments of a trapezoid intersect:
| In[5]:= |
| Out[5]= |
Determine an edge-case degeneracy:
| In[6]:= |
| Out[6]= |
Show it:
| In[7]:= |
| Out[7]= | 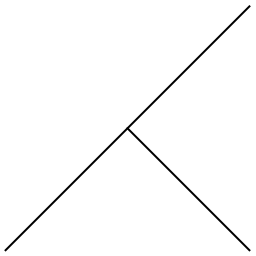 |
SegmentIntersectionQ works in 3D:
| In[8]:= | ![line1 = Line[{{0, 0, 0}, {0, 8, 8}}];
line2 = Line[{{-4, 4, 4}, {4, 4, 4}}];
ResourceFunction["SegmentIntersectionQ"][line1, line2]](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/038211311bde7318.png) |
| Out[10]= |
Show the lines:
| In[11]:= |
| Out[11]= | 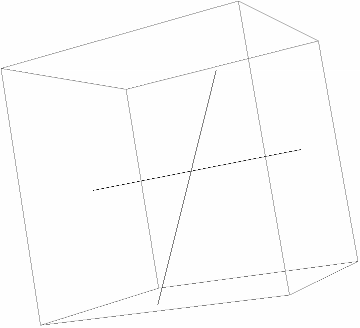 |
Various 2D intersections:
| In[12]:= | ![ResourceFunction[
"SegmentIntersectionQ"] /@ {(*Share an endpoint*){{{0, 0}, {1, 0}}, {{1, 0}, {1, 1}}},(*Touch at a corner*){{{0, 0}, {1, 1}}, {{1, 1}, {2, 2}}},(*Overlap on a side*){{{1, 0}, {3, 0}}, {{2, 0}, {3, 0}}},(*Colinear vertical overlap*){{{2, 1}, {2,
3}}, {{2, 2}, {2, 3}}},(*Same segment,
reversed*){{{0, 0}, {1, 1}}, {{1, 1}, {0, 0}}},(*Endpoint touch diagonally*){{{0, 3}, {3, 0}}, {{3, 0}, {3,
1}}},(*Exact overlap*){{{1, 2}, {2, 2}}, {{1, 2}, {2, 2}}},(*Colinear with interior point overlap*){{{0, 0}, {2, 0}}, {{1, 0}, {2, 0}}},(*Share an endpoint vertically*){{{3, 1}, {3, 2}}, {{3, 2}, {3, 3}}},(*Share a middle point*){{{1, 1}, {3, 1}}, {{2, 1}, {2, 3}}}}](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/2846cf49e8fe6165.png) |
| Out[12]= |
Various 2D non-intersections:
| In[13]:= | ![ResourceFunction[
"SegmentIntersectionQ"] /@ {(*Parallel horizontal,
different y*){{{0, 0}, {3, 0}}, {{0, 1}, {3, 1}}},(*Parallel vertical,
different x*){{{0, 0}, {0, 3}}, {{1, 0}, {1, 3}}},(*Same slope,
offset*){{{0, 0}, {2, 2}}, {{0, 1}, {2, 3}}},(*Skewed,
miss*){{{0, 0}, {1, 2}}, {{2, 0}, {3, 1}}},(*Disjoint colinear horizontally*){{{0, 0}, {1, 0}}, {{2, 0}, {3, 0}}},(*Disjoint colinear vertically*){{{0, 0}, {0, 1}}, {{0, 2}, {0, 3}}},(*Almost meeting at a point,
but miss*){{{0, 0}, {1, 1}}, {{1, 2}, {2, 3}}},(*Rectangle sides,
opposite edges*){{{0, 0}, {0, 3}}, {{3, 0}, {3, 3}}},(*Parallel diagonals,
no touch*){{{0, 0}, {2, 2}}, {{1, 0}, {3, 2}}},(*T shape,
missing by a gap*){{{0, 0}, {2, 0}}, {{1, 1}, {1, 2}}},(*Misaligned "X" shape*){{{0, 0}, {1, 1}}, {{1, 0}, {2, 1}}}}](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/4abebcdd5c0103c4.png) |
| Out[13]= |
Various 3D intersections:
| In[14]:= | ![ResourceFunction[
"SegmentIntersectionQ"] /@ {(*1. Interior intersection in XY plane*){{{0, 0, 0}, {3, 0, 0}}, {{1, -1, 0}, {1, 1, 0}}},(*2. Interior intersection in XZ plane*){{{0, 0, 0}, {3, 0, 0}}, {{1, 0, -1}, {1, 0, 1}}},(*3. Interior intersection in YZ plane*){{{0, 0, 0}, {0, 3, 0}}, {{0, 1, -1}, {0, 1, 1}}},(*4. Diagonal cross in XY plane*){{{0, 0, 0}, {3, 3, 0}}, {{0, 3, 0}, {3, 0, 0}}},(*5. Diagonal cross in XZ plane*){{{0, 0, 0}, {3, 0, 3}}, {{0, 0, 3}, {3, 0, 0}}},(*6. Diagonal cross in YZ plane*){{{0, 0, 0}, {0, 3, 3}}, {{0, 0, 3}, {0, 3, 0}}},(*7. Coplanar intersection,
off axis*){{{0, 0, 0}, {2, 1, 0}}, {{1, -1, 0}, {1, 2, 0}}},(*8. Touching at endpoint*){{{0, 0, 0}, {1, 0, 0}}, {{1, 0, 0}, {2, 1, 1}}},(*9. Intersecting along colinear overlap*){{{0, 0, 0}, {2, 0, 0}}, {{1, 0, 0}, {3, 0, 0}}},(*10. Short intersection at shared midpoint*){{{0, 0, 0}, {2, 2, 2}}, {{1, 1, 1}, {3, 3, 3}}},(*11. Cross in space at an interior point*){{{0, 0, 0}, {2, 2, 2}}, {{2, 0, 0}, {0, 2, 2}}},(*12. Intersect at center of rectangle*){{{0, 0, 0}, {2, 0, 0}}, {{1, -1, 0}, {1, 1, 0}}}}](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/129e2d19215c0c43.png) |
| Out[14]= |
Various 3D non-intersections:
| In[15]:= | ![ResourceFunction[
"SegmentIntersectionQ"] /@ {(*1. Colinear but disjoint along X-
axis*){{{0, 0, 0}, {1, 0, 0}}, {{2, 0, 0}, {3, 0, 0}}},(*2. Coplanar,
parallel in XY plane*){{{0, 0, 0}, {1, 0, 0}}, {{0, 1, 0}, {1, 1, 0}}},(*3. Coplanar,same line,reversed order,
no overlap*){{{0, 0, 0}, {1, 1, 0}}, {{2, 2, 0}, {3, 3, 0}}},(*4. Skew,completely non-
coplanar*){{{0, 0, 0}, {1, 0, 0}}, {{0, 1, 1}, {1, 1, 2}}},(*5. Skew with same XY but separated Z*){{{0, 0, 0}, {1, 1, 0}}, {{0, 0, 1}, {1, 1, 1}}},(*6. Touch only at extension (not segment)*){{{0, 0, 0}, {1,
1, 0}}, {{2, 2, 0}, {3, 3, 0}}},(*7. Parallel in X,
but offset in Y and Z*){{{0, 0, 0}, {1, 0, 0}}, {{0, 1, 1}, {1, 1, 1}}},(*8. Skew T-shape,
tip misses base*){{{0, 0, 0}, {2, 0, 0}}, {{1, 1, 1}, {1, 2, 2}}},(*9. Close,nearly crossing in space,
but miss*){{{0, 0, 0}, {1, 1, 1}}, {{1, 0, 0}, {2, 1, 0}}},(*10. Parallel diagonals in XY plane,
different Z*){{{0, 0, 0}, {2, 2, 0}}, {{0, 0, 1}, {2, 2, 1}}},(*11. Rectangle opposite edges*){{{0, 0, 0}, {0, 3, 0}}, {{3, 0, 0}, {3, 3, 0}}},(*12. Almost touching corner but miss*){{{0, 0, 0}, {1, 1, 1}}, {{1, 1, 1.1}, {2, 2, 2}}}}](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/0d7e7cd8ad74702b.png) |
| Out[15]= |
Find disjoint segment pairs from a set of twelve points:
| In[16]:= | ![points = {{12, 15}, {23, 23}, {15, 10}, {19, 0}, {0, 19}, {9, 17}, {4,
18}, {16, 13}, {19, 18}, {25, 25}, {16, 17}, {17, 6}};
lines = Subsets[points, {2}]; linepairs = Select[Subsets[lines, {2}], DisjointQ @@ # &];](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/40cd8568b79ab7e6.png) |
With timings, find all segment pairs that intersect:
| In[17]:= |
| Out[17]= |
With timings, use RegionIntersection to find all segment pairs that intersect:
| In[18]:= | ![AbsoluteTiming[
crossingsR = Select[linepairs, Head[RegionIntersection[Region[Line[#[[1]]]], Region[Line[#[[2]]]]][[1]]] === Point &];]](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/589a76cd29402117.png) |
| Out[18]= |
Note the timing difference and compare the two results:
| In[19]:= |
| Out[19]= |
Show the results:
| In[20]:= | ![crosses = ResourceFunction["LineIntersection"] /@ crossings;
Graphics[{Line /@ Complement[lines, Flatten[crossings, 1]], Thin, Line /@ lines,
Red, Point[crosses], Blue, Point[points]}]](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/7003b6ae02b6d275.png) |
| Out[21]= | 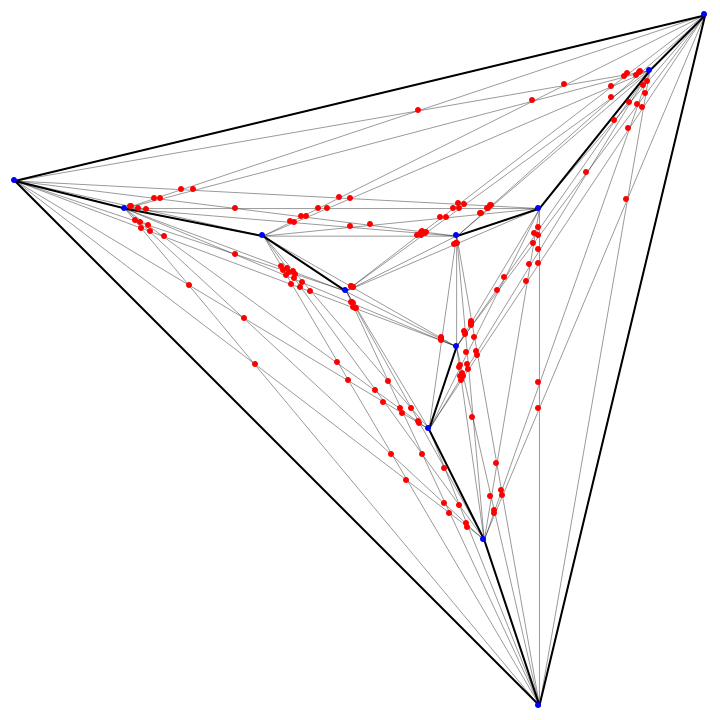 |
Various bad inputs will not work:
| In[22]:= |
| Out[22]= |
Degenerate overlaps are returned as intersections:
| In[23]:= |
| Out[23]= |
Of the 210 possible disjoint pairs of the 21 segments defined by 7 points, pick out those that intersect:
| In[24]:= | ![points = {{4, 3}, {6, 4}, {3, 3}, {0, 5}, {5, 1}, {5, 0}, {7, 5}};
lines = Subsets[points, {2}]; linepairs = Select[Subsets[lines, {2}], DisjointQ @@ # &];
crossings = Select[linepairs, ResourceFunction["SegmentIntersectionQ"]]](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/24cec61d66c47532.png) |
| Out[25]= |  |
Nine crossings happens to be the minimum for seven points. Show it:
| In[26]:= | ![crosses = ResourceFunction["LineIntersection"] /@ crossings;
Graphics[{Line /@ Complement[lines, Flatten[crossings, 1]], Thin, Line /@ lines,
Red, Point[crosses], Blue, Point[points]}]](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/5ed9a177ee4d57b5.png) |
| Out[27]= | 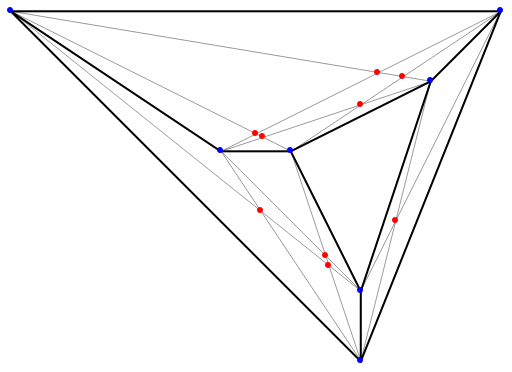 |
For 27 points, the minimal number of intersections is 6180. Set it up:
| In[28]:= | ![points = {{337, 670}, {393, 529}, {446, 576}, {293, 393}, {263, 352}, {447, 576}, {409, 573}, {421, 545}, {461, 570}, {415, 585}, {423, 547}, {476, 574}, {409, 574}, {394, 604}, {586, 596}, {398, 601}, {183, 239}, {669, 610}, {359, 642}, {25, 33}, {494, 579}, {382, 612}, {0, 0}, {513, 585}, {370, 629}, {103,
135}, {568, 593}};
lines = Subsets[points, {2}]; linepairs = Select[Subsets[lines, {2}], DisjointQ @@ # &];](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/5d129cc8fc468aca.png) |
Find the crossings:
| In[29]:= |
| Out[29]= |
Show it:
| In[30]:= | ![crosses = ResourceFunction["LineIntersection"] /@ crossings;
Graphics[{Line /@ Complement[lines, Flatten[crossings, 1]], Thin, Line /@ lines,
Red, Point[crosses], Blue, Point[points]}]](https://www.wolframcloud.com/obj/resourcesystem/images/3a7/3a79377d-30ef-4a5c-acc5-91f876af6e0d/4ad535b4a1273073.png) |
| Out[31]= | 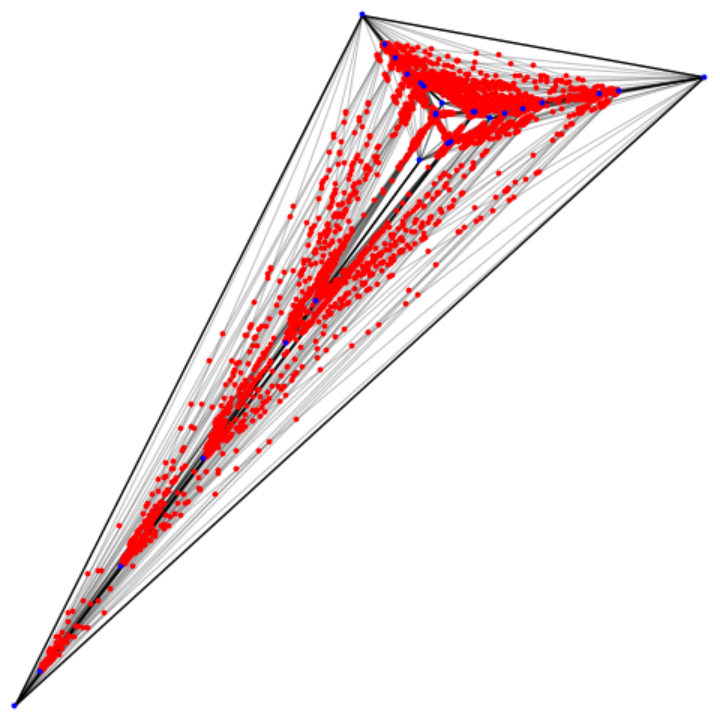 |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License