Function Repository Resource:

SecantLine

Compute properties of the secant line to a curve between two points

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["SecantLine"][expr,{x,x₁,x₂},{y,y₁,y₂}]

returns an association of properties of the secant line to expr, viewed as an equation in x and y, between the points {x₁,y₁} and {x₂,y₂}.

ResourceFunction["SecantLine"][expr,{x,x₁,x₂},{y,y₁,y₂},prop]

returns the value of the secant line property prop.

ResourceFunction["SecantLine"][expr,{x,x₁,x₂},y]

returns information relating to one, among possibly several, of the secant lines to expr between x=x₁ and x=x₂.

ResourceFunction["SecantLine"][expr,x,{y,y₁,y₂}]

returns information relating to one, among possibly several, of the secant lines to expr between y=y₁ and y=y₂.

Details

Allowed values of prop are:

"SlopeInterceptEquation"

equation of the secant line in slope-intercept form

"StandardFormEquation"

equation of the secant line in standard form

"PointSlopeEquation"

equation of the secant line in point-slope form

"Slope"

slope of the secant line

"PointsOfIntersection"

points between which the secant line is computed

"HorizontalIntercept"

horizontal intercept for the secant line equation

"VerticalIntercept"

vertical intercept for the secant line equation

"Plot"

plot of the secant line equation

All

Association of information returning all allowed properties

If expr does not have head Equal, then expr is treated as an expression defining y in terms of x. In other words, ResourceFunction["SecantLine"][expr,{x,a},y,…] is equivalent to ResourceFunction["SecantLine"][y==expr,{x,a},y,…] if expr has a head other than Equal.

If only one coordinate of the intersection points is given, the other coordinates are inferred. For expressions that are multivalued at the given value of x or y, information on only one of potentially several secant lines is returned.

Examples

Basic Examples (2)

Compute the slope-intercept equation of the secant line to a curve between two points:

In[1]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ y == x^2 + 3, {x, 1, 4}, y, "SlopeInterceptEquation"]$

Out[1]=

Visualize this result:

In[2]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][y == x^2 + 3, {x, 1, 4}, y, "Plot"]$

Out[2]=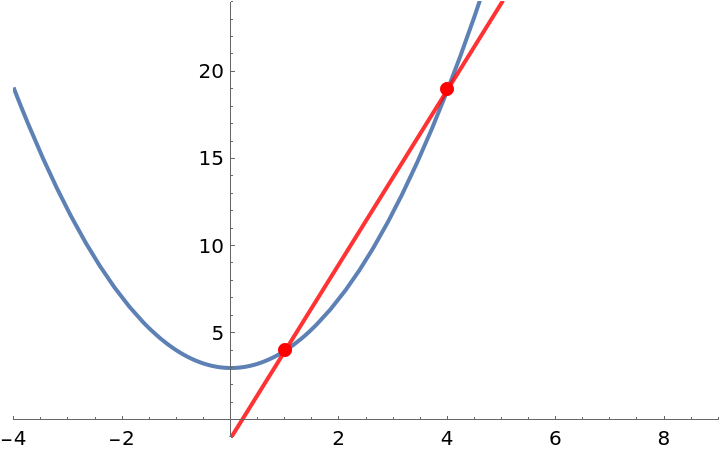

Compute the slope of this secant line:

In[3]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][y == x^2 + 3, {x, 1, 4}, y, "Slope"]$

Out[3]=

Compute the horizontal intercept of this secant line:

In[4]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ y == x^2 + 3, {x, 1, 4}, y, "HorizontalIntercept"]$

Out[4]=

Get the standard-form equation of this secant line:

In[5]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ y == x^2 + 3, {x, 1, 4}, y, "StandardFormEquation"]$

Out[5]=

Get an Association of properties of a secant line to a curve:

In[6]:=

Out[6]=

Get just the point-slope equation of this secant line:

In[7]:=

Out[7]=

Scope (1)

The first argument to SecantLine can be an implicit definition of a curve:

In[8]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][x^2 + y^3 == 0, {x, 1, 8}, {y, -1, -4}]$

Out[8]=

Properties and Relations (2)

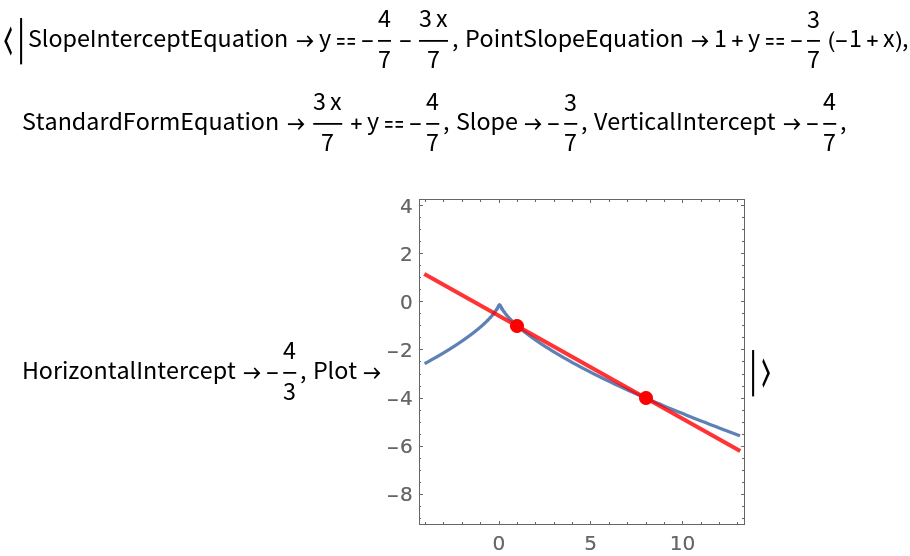If a secant line is parallel to a coordinate axis, its intercept with that axis is None:

In[9]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ x^2 + 3, {x, -4, 4}, y, "HorizontalIntercept"]$

Out[9]=

Requesting secant line information about a point that is not on the curve will result in an error message:

In[10]:=

Out[10]=

Possible Issues (2)

If one coordinate is not specified, information on only one of the possible secant lines at the given coordinate values is returned:

In[11]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][x^2 + y^2 == 1, {x, 0, 1}, y]$

Out[11]=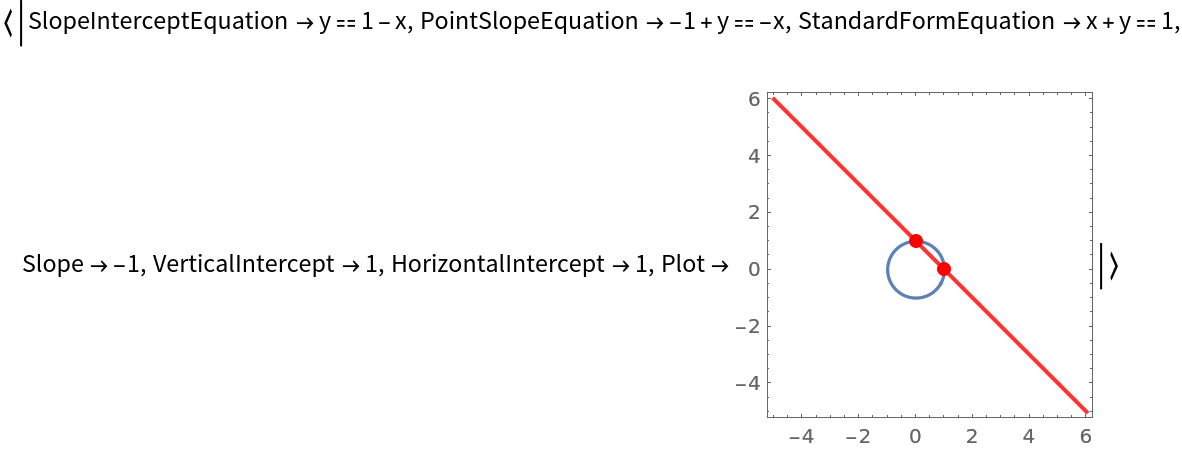

The slope of a vertical secant line cannot be computed:

In[12]:=

$ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][x^2 + y^2 == 1, {x, 0, 0}, {y, 1, -1}]$

Out[12]=

Neat Examples (1)

Use SecantLine and the resource function TangentLine within Manipulate to create an interactive tool that demonstrates the relationship between the tangent line to a curve at a point x=-1 and the secant line between x=-1 and another point that approaches x=-1:

In[13]:=

$Manipulate[ Show[{Quiet@ ResourceFunction[ "SecantLine", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][x^2, {x, -1, a}, y, "Plot"], ResourceFunction["TangentLine"][x^2, {x, -1}, y, "Plot"]}, PlotRange -> {{-2, 2}, {-2, 6}}, PlotPoints -> 1000], {a, 1.75, -.99, -1/10}]$

Out[14]=

Publisher

Wolfram|Alpha Math Team

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

2.1.0 – 04 August 2023
2.0.0 – 23 March 2023
1.0.0 – 29 March 2022

Related Resources

Author Notes

To view the full source code for SecantLine, evaluate the following: