Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SchurS

Source Notebook

Evaluate the Schur polynomial corresponding to an integer partition

Contributed by: Jan Mangaldan

ResourceFunction["SchurS"][p,{x1,…,xn}]

gives the Schur polynomial sp(x1,…,xn) corresponding to the integer partition p in the variables x1,…,xn.

Details

Schur polynomials are also called Schur functions.
The Schur polynomial is defined as the sum , where T ranges over all the semi-standard Young tableaux with shape corresponding to the integer partition p, and the exponents tj count the number of occurences of the number j in the semi-standard Young tableau T.
The Schur polynomials are the characters of polynomial irreducible representations of the general linear groups in representation theory.
The Schur polynomial is a symmetric polynomial of n variables, and is thus invariant under any permutation of its variables.
The integer partition p should be a list of weakly decreasing non-negative integers.
The degree of ResourceFunction["SchurS"][p,{x1,…,xn}] is equal to Total[p].
The Schur polynomials form a basis for the symmetric polynomials.

Examples

Basic Examples (1) 

A Schur polynomial in two variables:

In[1]:=
ResourceFunction["SchurS"][{2, 1}, {x, y}]
Out[1]=

Scope (2) 

Generate all partitions of 8 into at most 3 integers:

In[2]:=
parts = IntegerPartitions[8, 3]
Out[2]=

Generate all Schur polynomials in three variables of degree 8:

In[3]:=
Table[ResourceFunction["SchurS"][p, {x, y, z}], {p, parts}]
Out[3]=

Applications (4) 

Count the number of semi-standard Young tableaux of shape (4 2 1 1), with entries taken from the numbers 1 to 4:

In[4]:=
ResourceFunction["SchurS"][{4, 2, 1, 1}, ConstantArray[1, 4]]
Out[4]=

Verify Jacobi's bialternant formula for the Schur polynomial:

In[5]:=
p = {4, 3, 1, 1}; vars = {x, y, z, w}; ResourceFunction["SchurS"][p, vars] == PolynomialReduce[ Det[Outer[Power, vars, PadRight[p, Length[vars]] + Range[Length[vars] - 1, 0, -1]]], Det[VandermondeMatrix[vars]], vars][[1, 1]] // FullSimplify
Out[6]=

Generate all monomial symmetric polynomials of degree 5:

In[7]:=
parts = IntegerPartitions[5]; vars = {x, y, z, u, v}; Short[msp = Table[Last[ FactorTermsList[AugmentedSymmetricPolynomial[p, vars]]], {p, parts}]]
Out[8]=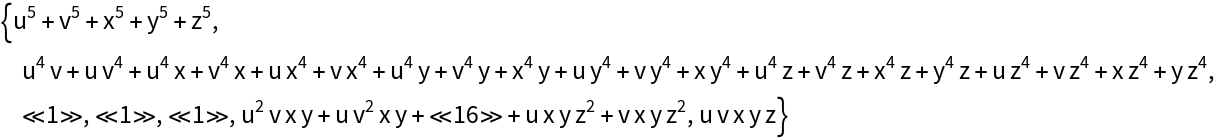

Generate the Kostka numbers as the coefficients that arise when the Schur polynomial is expanded in the monomial symmetric basis:

In[9]:=
PolynomialReduce[ResourceFunction["SchurS"][ \!\(\*SubscriptBox[\(parts\), \(\(\[LeftDoubleBracket]\)\(2\)\(\[RightDoubleBracket]\)\)]\), vars], msp, vars]
Out[9]=

The Littlewood-Richardson rule states that the product of two Schur polynomials can be expressed as a linear combination of Schur polynomials with integer coefficients. Generate the product from the original example by Littlewood and Richardson:

In[10]:=
vars = {\[FormalX][1], \[FormalX][2], \[FormalX][3], \[FormalX][ 4], \[FormalX][5], \[FormalX][6]}; p1 = {4, 3, 1}; p2 = {2, 2, 1}; Short[prod = ResourceFunction["SchurS"][p1, vars] ResourceFunction["SchurS"][p2, vars]]
Out[11]=

Use PolynomialReduce to find the coefficients for the Schur polynomial terms of the product (this might take a while to evaluate):

In[12]:=
pList = IntegerPartitions[Total[p1] + Total[p2], Length[vars]]; basis = Table[ResourceFunction["SchurS"][p, vars], {p, pList}]; AbsoluteTiming[{coef, rem} = PolynomialReduce[prod, basis, vars]]
Out[13]=

Show the mapping between the nonzero coefficients and their corresponding partitions:

In[14]:=
cas = Select[AssociationThread[pList -> coef], Positive]
Out[14]=

Reconstruct the original polynomial:

In[15]:=
Total[KeyValueMap[#2 ResourceFunction["SchurS"][#1, vars] &, cas]] == prod // Expand
Out[15]=

Properties and Relations (1) 

PolynomialReduce can be used to find the coefficients for the expansion of any symmetric polynomial in the Schur basis:

In[16]:=
poly = x^4 + y^4 + z^4; basis = Table[ ResourceFunction["SchurS"][p, {x, y, z}], {p, IntegerPartitions[4, 3]}]; coef = First[PolynomialReduce[poly, basis, {x, y, z}]]
Out[17]=

Version History

  • 1.0.0 – 10 April 2023

Source Metadata

  • Citation:
    • Demmel J., Koev P., "Accurate and Efficient Evaluation of Schur and Jack Functions." Mathematics of Computation, vol. 75, no. 253, 223–239, 2006.
      DOI: 10.1090/S0025-5718-05-01780-1
    • Macdonald I.G., Symmetric Functions and Hall Polynomials, 2nd ed. Oxford, England: Oxford University Press, 1995.

Related Resources

Author Notes

SchurS uses the dual Jacobi-Trudi determinant (also known as the Nägelsbach–Kostka formula) for evaluating the Schur polynomial.

License Information