Basic Examples (2) 

The fifth Schett polynomial:

In[1]:=

Out[1]=

The fifth Schett polynomial with specified variables:

In[2]:=

Out[2]=

Scope (1) 

Some coefficients of n^thSchett recurrence grows as rapidly as n!. For large index, it is convenient to use SparseArray to represent the polynomial:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Applications (1) 

The Schett recurrence formula significantly speeds up the computation for high order terms in Taylor series for Jacobi elliptic functions:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

Properties and Relations (4) 

The sum of the coefficients in S_n is equal to n!:

In[7]:=

Out[7]=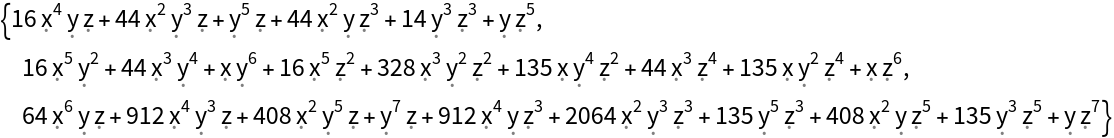

In[8]:=

Out[8]=

The coefficient of the Taylor series for JacobiSN is contained in the first column of the compact coefficient matrix for the Schett polynomial:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

The denominators in the Taylor series are factorials of odd numbers:

In[11]:=

Out[11]=

The coefficient of Taylor series for JacobiCN is contained in the first row of the compact coefficient matrix:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

The denominators in the Taylor series are factorials of even numbers:

In[14]:=

Out[14]=

The coefficient of Taylor series for JacobiDN is contained in the first row of the compact coefficient matrix:

In[15]:=

Out[15]=

In[16]:=

Out[16]=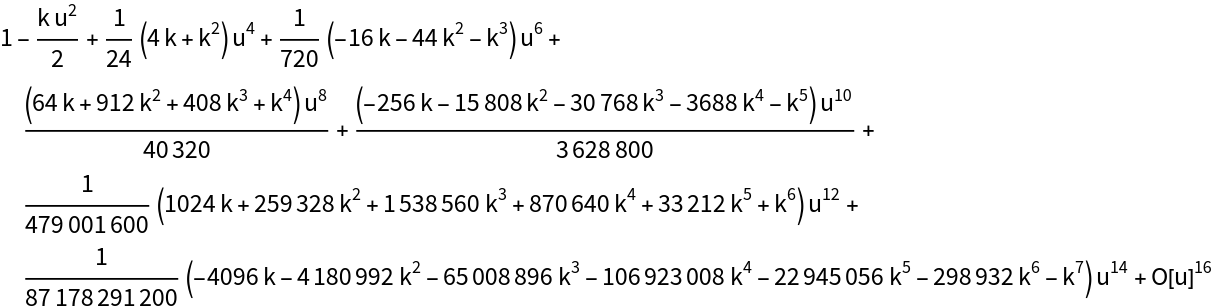

The denominators in the Taylor series are just factorials of even numbers:

In[17]:=

Out[17]=

Possible Issues (3) 

The coefficient matrix is not defined for indices less than 2:

In[18]:=

Out[18]=

The (i,j)^th term in the coefficient matrix does not represent the coefficient of xⁱy^jz^n-i-j in the corresponding polynomial:

In[19]:=

Out[20]=

In[21]:=

Out[21]=

Instead, a general index conversion formula is applied: (i,j) → x^2j-1y^2i-2z^n+4-2i-2j for even n and (i,j) → x^2j-2y^2i-1z^n+4-2i-2j for odd n. For instance, 408 in S₈ above occurs at {1,2} and {4,2}. The exponent for the term in the polynomial is:

In[22]:=

Out[22]=

In this example one finds that 408 is the coefficient for x³y⁰z⁶ and x³y⁶z⁰.

SchettPolynomial use memoization to speed up computation and the memory is not automatically released. Use "Reset" to free up memory space:

In[23]:=