Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ScatteredInterpolation

Source Notebook

Perform interpolation in n-dimensional space for irregularly spaced data

Contributed by: Sander Huisman

ResourceFunction["ScatteredInterpolation"][{pts1→v1,pts2→v2,…},{x1,x2,…}]

interpolates values at xi assuming the function take values vi at points ptsi.

ResourceFunction["ScatteredInterpolation"][{pts1→v1,pts2→v2,…},{x1,x2,…},p]

uses the power parameter p for the weighting.

ResourceFunction["ScatteredInterpolation"][{pts1→v1,pts2→v2,…},{x1,x2,…},p,nbspec]

uses the neighborhood specification nbspec.

ResourceFunction["ScatteredInterpolation"][{{{x1,y1},v1},{{x2,y2},v2},…},…]

interpolates data given as position-value pairs.

ResourceFunction["ScatteredInterpolation"][{pts1→v1,pts2→v2,…},p,nbspec]

represents an operator form that can be applied to the points {x1,x2,…}.

Details and Options

ResourceFunction["ScatteredInterpolation"] implements the inverse distance weighting (IDW) algorithm for multivariate interpolation of scattered data in n dimensions.
The second argument should be a list of points.
The interpolated value is given by where .
The default value of p is 2.
The neighborhood specification nbspec has a default value of All. nbspec takes the forms supported by Nearest. An integer n means the nearest n data points are used. A specification of the form {a,b} means that within a radius b, at most a points are used, where a is an integer or All, such that all points within a radius b are used.
ResourceFunction["ScatteredInterpolation"] supports the DistanceFunction option where the default is given by Norm[#1-#2]&.
When xi corresponds precisely with ptsj, ptsj will be returned. If multiple values are known at that point, the mean of those values is returned.

Examples

Basic Examples (3) 

Find scattered interpolations of a few points in 1D:

In[1]:=
ResourceFunction[ "ScatteredInterpolation"][{1 -> 1, 2 -> 2, 3 -> 3}, {1.1, 1.2, 2.2, 2.4}]
Out[1]=

Interpolate in 1D:

In[2]:=
ref = {4.8899913499492556` -> 0.9031326446751295`, 1.392792312302646` -> 0.8452211334302036`, 3.7329747819370276` -> 0.7506691817125113`, 3.6344473306632317` -> 0.5609777119243873`, 4.502776333137257` -> 0.2861928835103029`, 9.308025498446717` -> 0.8910605626408117`, 1.6139856617732704` -> 0.5113662122131557`, 1.887782604676982` -> 0.7338499915592447`, 3.0719573664861617` -> 0.8498335301543973`, 3.230905136858455` -> 0.6202210246844337`, 4.684791130057821` -> 0.6993738414887227`, 6.442677446169533` -> 0.6045567909822067`, 6.10605611091858` -> 0.23505337764021728`, 5.006465834341876` -> 0.06849979808894058`, 9.959154534492047` -> 0.6370358021750766`}; Short[out = ResourceFunction["ScatteredInterpolation"][ref, Subdivide[0, 10, 300]]]
Out[3]=

Show the results along with the original points:

In[4]:=
ListLinePlot[out, AspectRatio -> 1/4, Epilog -> {PointSize[0.01], Point[List @@@ ref]}]
Out[4]=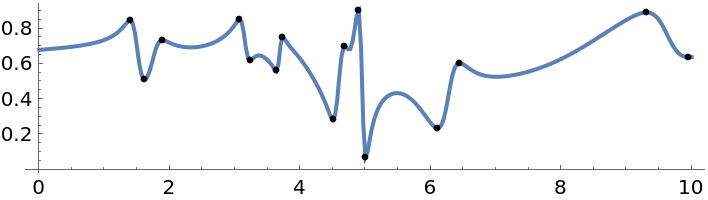

Interpolate in 2D:

In[5]:=
SeedRandom[1337]; tmp = Table[RandomPoint[Rectangle[]] -> RandomReal[], 15]; xs = Catenate@Table[{i, j}, {i, Subdivide[50]}, {j, Subdivide[50]}]; Short[out = ResourceFunction["ScatteredInterpolation"][tmp, xs, 3, All]]
Out[8]=

Plot the resulting surface along with the original points:

In[9]:=
Show[{ListPlot3D[Flatten /@ out], Graphics3D[{Black, Sphere[Append @@@ tmp, 0.02]}]}, BoxRatios -> Automatic]
Out[9]=

Scope (2) 

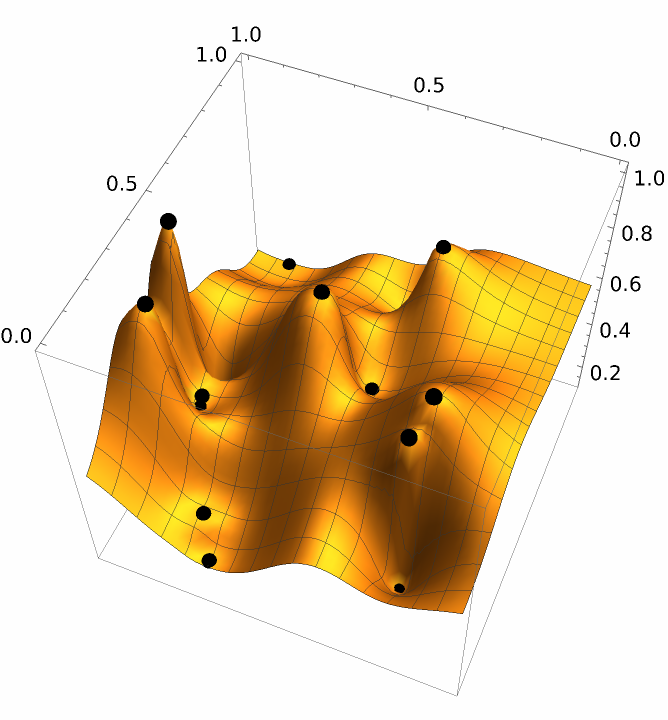Interpolate 5D scattered data:

In[10]:=
SeedRandom[1337]; tmp = Table[RandomReal[{0, 1}, 5] -> RandomReal[], 15]; xs = {ConstantArray[0.5, 5]}; ResourceFunction["ScatteredInterpolation"][tmp, xs, 3, All]
Out[13]=

Alternatively it can be specified in an operator form:

In[14]:=
ResourceFunction["ScatteredInterpolation"][tmp, 3, All][xs]
Out[14]=

Options (1) 

Use a different DistanceFunction:

In[15]:=
SeedRandom[1234]; tmp = Table[RandomPoint[Rectangle[]] -> RandomReal[], 15]; xs = Catenate@Table[{i, j}, {i, Subdivide[50]}, {j, Subdivide[50]}]; out = ResourceFunction["ScatteredInterpolation"][tmp, xs, 4, All, DistanceFunction -> ManhattanDistance]; Show[{ListPlot3D[Flatten /@ out], Graphics3D[{Black, Sphere[Append @@@ tmp, 0.02]}]}, BoxRatios -> Automatic]
Out[19]=

Properties and Relations (1) 

The built-in Interpolation function cannot recreate the results from ScatteredInterpolation:

In[20]:=
SeedRandom[1337]; tmp = Table[RandomPoint[Rectangle[]] -> RandomReal[], 15]; xs = Catenate@Table[{i, j}, {i, Subdivide[50]}, {j, Subdivide[50]}]; out = ResourceFunction["ScatteredInterpolation"][tmp, xs, 3, All]; a = Show[{ListPlot3D[Flatten /@ out], Graphics3D[{Black, Sphere[Append @@@ tmp, 0.02]}]}, BoxRatios -> Automatic, ImageSize -> 300]; dt = Quiet[{#, Interpolation[List @@@ tmp, InterpolationOrder -> 1] @@ #} & /@ xs]; b = Show[{ListPlot3D[Flatten /@ dt], Graphics3D[{Black, Sphere[Append @@@ tmp, 0.02]}]}, BoxRatios -> {1, 1, 1}, ImageSize -> 300]; dt = Quiet[{#, Interpolation[List @@@ tmp, InterpolationOrder -> All] @@ #} & /@ xs]; c = Show[{ListPlot3D[Flatten /@ dt], Graphics3D[{Black, Sphere[Append @@@ tmp, 0.02]}]}, BoxRatios -> {1, 1, 1}, ImageSize -> 300]; Grid[{{"ScatteredInterpolation", "Interpolation with order 1", "Interpolation with order All"}, {a, b, c}}]
Out[29]=

Possible issues (1) 

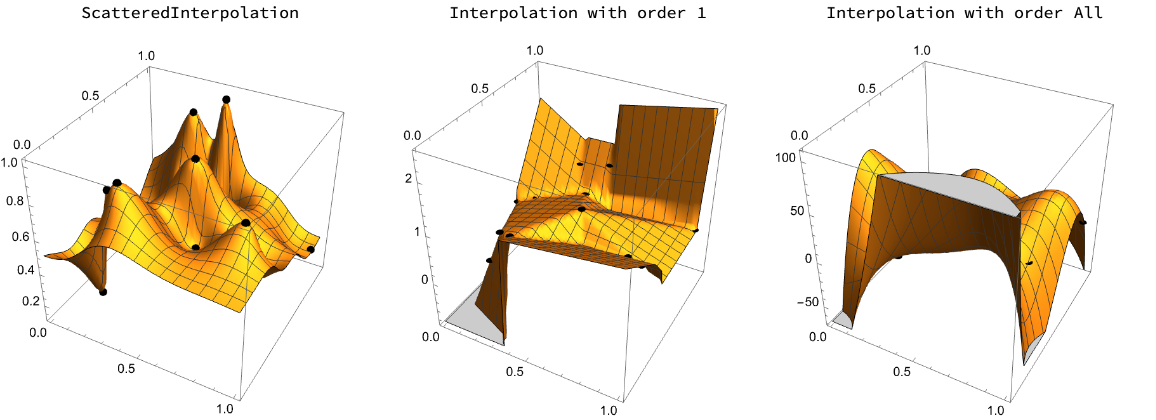If a specific radius is given, large gaps in the data might prevent the possibility of interpolation; moreover the function can be discontinuous in some places:

In[30]:=
ref = {4.8899913499492556` -> 0.9031326446751295, 1.392792312302646 -> 0.8452211334302036, 3.7329747819370276` -> 0.7506691817125113, 3.6344473306632317` -> 0.5609777119243873, 4.502776333137257 -> 0.2861928835103029, 9.308025498446717 -> 0.8910605626408117, 1.6139856617732704` -> 0.5113662122131557, 1.887782604676982 -> 0.7338499915592447, 3.0719573664861617` -> 0.8498335301543973, 3.230905136858455 -> 0.6202210246844337, 4.684791130057821 -> 0.6993738414887227, 6.442677446169533 -> 0.6045567909822067, 6.10605611091858 -> 0.23505337764021728`, 5.006465834341876 -> 0.06849979808894058, 9.959154534492047 -> 0.6370358021750766}; out = ResourceFunction["ScatteredInterpolation"][ref, Subdivide[0, 10, 300], 4, {All, 0.7}]; ListLinePlot[out, AspectRatio -> 1/4, Epilog -> {PointSize[0.01], Point[List @@@ ref]}, ImageSize -> 800]
Out[31]=

Neat Examples (1) 

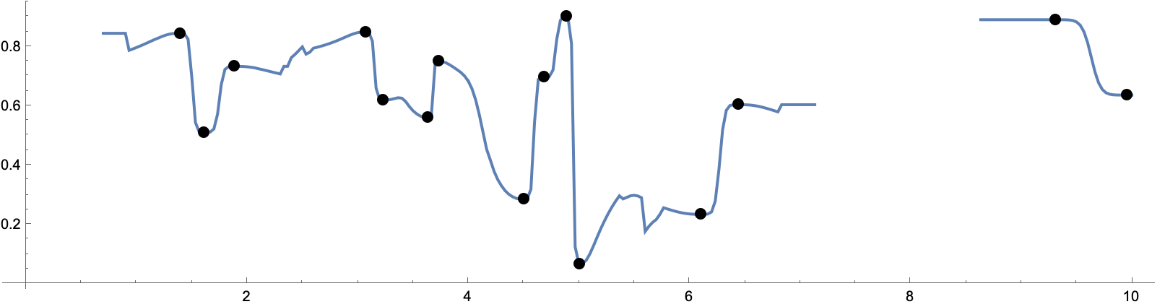High p basically gives the value of the nearest point, creating a Voronoi tessellation:

In[32]:=
SeedRandom[1337]; tmp = Table[RandomPoint[Rectangle[]] -> RandomReal[], 15]; xs = Catenate@Table[{i, j}, {i, Subdivide[80]}, {j, Subdivide[80]}]; out = ResourceFunction["ScatteredInterpolation"][tmp, xs, 30]; Show[{ListPlot3D[Flatten /@ out], Graphics3D[{Black, Sphere[Append @@@ tmp, 0.02]}]}, BoxRatios -> Automatic]
Out[33]=

Publisher

SHuisman

Requirements

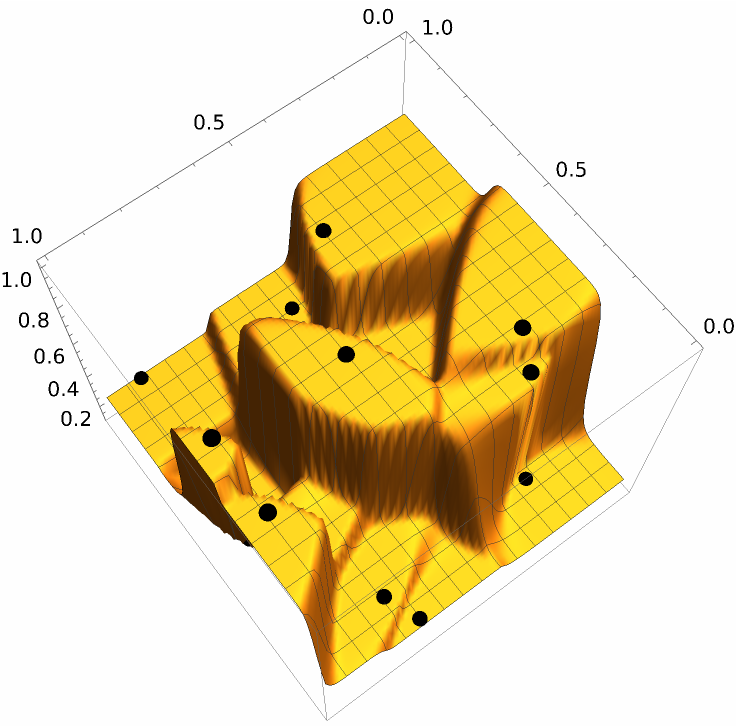Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 17 April 2024

Related Resources

License Information