Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Sandpile
Compute toppling trajectories of Abelian sandpiles on undirected finite multigraphs
Contributed by:
Phileas Dazeley-Gaist
ResourceFunction["SandpileTopple"][g] returns the sandpile g after toppling every unstable vertex once. | |
ResourceFunction["SandpileTopple"][g,n] returns the sandpile g after iteratively toppling g n times. | |
ResourceFunction["SandpileTopple"][g,n,"AllSteps"] returns a list of the results of toppling g 0 through n times. | |
ResourceFunction["SandpileTopple"][g,"Stabilize"] iteratively topple g until g not longer changes. | |
ResourceFunction["SandpileTopple"][g,"Stabilize","AllSteps"] returns a list of the results of toppling g until g longer changes. | |
ResourceFunction["SandpileTopple"][g,{"Stabilize",n}] iteratively topple g until g not longer changes, in up to n steps. | |
ResourceFunction["SandpileTopple"][g,{"Stabilize",n},"AllSteps"] returns a list of the results of toppling g until the result no longer changes, in at most n steps. |
Details and Options
SandpileTopple topples every unstable vertex of the sandpile graph g once at each toppling step.
A sandpile graph is a multigraph with zero-weighted or positively weighted vertices, and exactly one sink vertex, weighted “sink”. For the purposes of this function, sandpile graphs are assumed to be undirected. In a sandpile graph, vertices are points in space. Vertex weights represent amounts of sand at each of these points, and edges form the connections that allow sand to move from one vertex to another. Sandpile graph vertex weights are typically integers, which one can interpret as grains of sand, but can also be positive real numbers, analogous to continuous quantities of sand.
When the weight of a sandpile vertex is greater than or equal to its degree, the vertex is unstable, and will topple at the next toppling step. As it topples, it sends 1 to each of its adjacent vertices, except for the sink vertex, and loses the value of its degree from its weight. A sandpile vertex is stable if its weight is less than its degree. Stable vertices do not topple. The sink vertex does not participate in the toppling process.
A sandpile in which the sink is not connected to any of the vertices is a valid sandpile, but it is not guaranteed to ever reach a fixed point through iterated toppling. When the sink is connected to at least one non-sink vertex, iterated toppling will always yield a fixed point given enough iterations.
Use the "DeleteSink" option to remove the sink vertex from computed toppled graphs.
By default, SandpileTopple styles vertices according to their weight. Use ColorFunction to control the vertex colouring scheme.
To disable styling, set "StyleSandpile" to False. Doing so will save computational resources when computing long toppling sequences, toppling large graphs.
Examples
Basic Examples (3)
Topple a sandpile once:
| In[1]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexStyle -> {5 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 7 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 3 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 1 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 8 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 2 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 6 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 4 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 9 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 1.}, 0.25]}, InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 2.}, 0.25]}, InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 3.}, 0.25]}, InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 1.}, 0.25]}, InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 2.}, 0.25]}, InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 3.}, 0.25]}, InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 1.}, 0.25]}, InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 2.}, 0.25]}, InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 3.}, 0.25]}, InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/1ecc463fded4cbfd.png) |
| Out[1]= |  |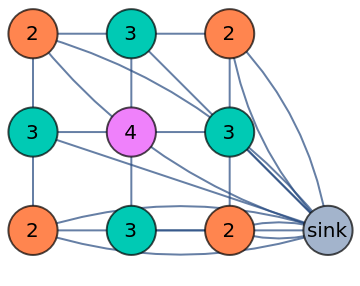
Topple a sandpile thrice:
| In[2]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexStyle -> {5 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 7 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 3 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 1 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 8 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 2 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 6 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 4 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 9 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 1.}, 0.25]}, InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 2.}, 0.25]}, InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 3.}, 0.25]}, InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 1.}, 0.25]}, InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 2.}, 0.25]}, InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 3.}, 0.25]}, InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 1.}, 0.25]}, InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 2.}, 0.25]}, InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 3.}, 0.25]}, InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\), 3]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/4c2d146dc6d9cadc.png) |
| Out[2]= |  |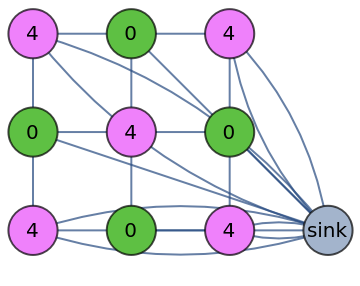
Topple a sandpile four times and return the complete list of toppling steps:
| In[3]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexStyle -> {5 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 7 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 3 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 1 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 8 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 2 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 6 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 4 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 9 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 1.}, 0.25]}, InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 2.}, 0.25]}, InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 3.}, 0.25]}, InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 1.}, 0.25]}, InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 2.}, 0.25]}, InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 3.}, 0.25]}, InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 1.}, 0.25]}, InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 2.}, 0.25]}, InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 3.}, 0.25]}, InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\), 4, "AllSteps"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/1076fd8f719a52ac.png) |
| Out[3]= |  |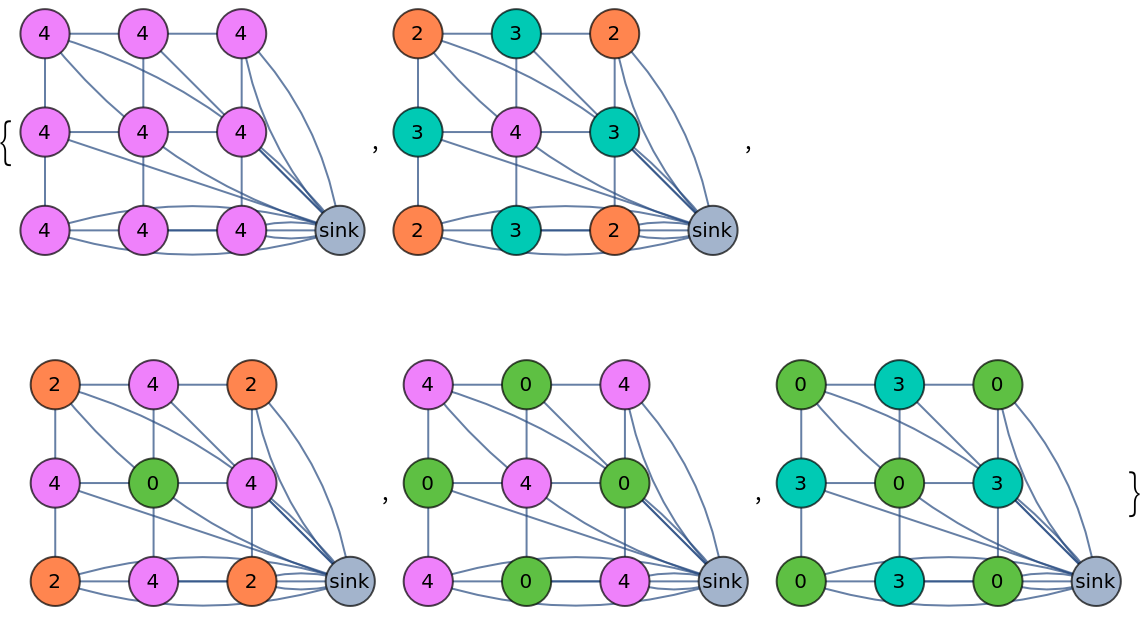
Topple a sandpile until results no longer change:
| In[4]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexStyle -> {5 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 7 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 3 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 1 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 8 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 2 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 6 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 4 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 9 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 1.}, 0.25]}, InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 2.}, 0.25]}, InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 3.}, 0.25]}, InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 1.}, 0.25]}, InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 2.}, 0.25]}, InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 3.}, 0.25]}, InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 1.}, 0.25]}, InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 2.}, 0.25]}, InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 3.}, 0.25]}, InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\), "Stabilize"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/30b379599cdf7180.png) |
| Out[4]= |  |
Topple a sandpile until results no longer change, and return the complete list of toppling steps:
| In[5]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexStyle -> {5 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 7 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 3 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 1 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 8 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 2 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 6 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 4 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 9 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 1.}, 0.25]}, InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 2.}, 0.25]}, InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 3.}, 0.25]}, InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 1.}, 0.25]}, InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 2.}, 0.25]}, InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 3.}, 0.25]}, InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 1.}, 0.25]}, InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 2.}, 0.25]}, InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 3.}, 0.25]}, InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\), "Stabilize", "AllSteps"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/4f6fccdf43cb4cd0.png) |
| Out[5]= |  |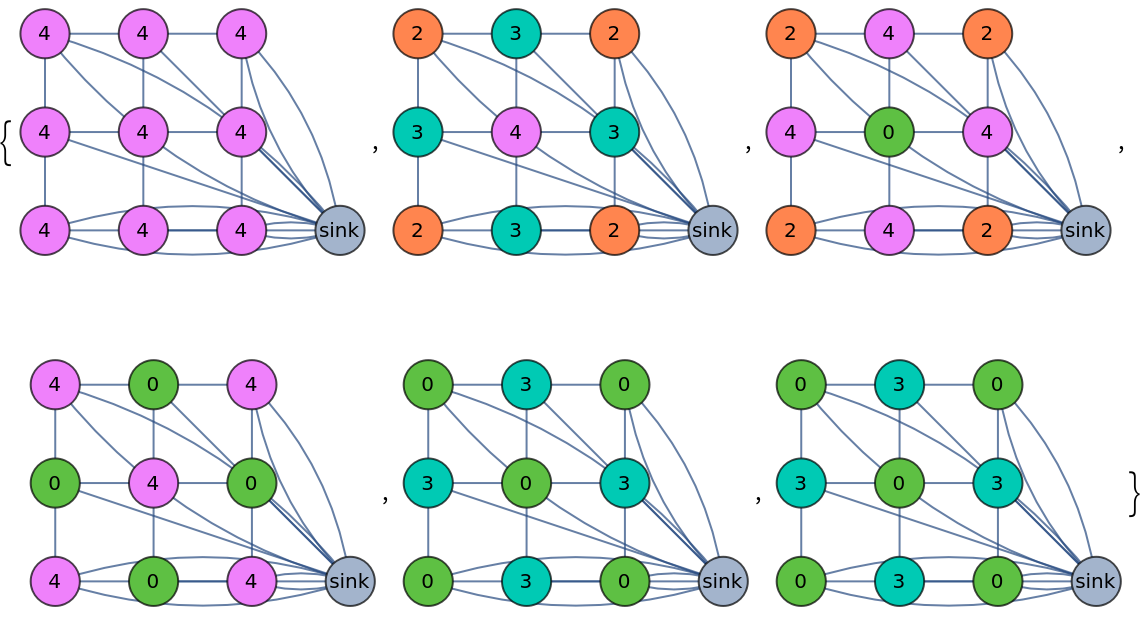
Find the fixed point of a sandpile toppling trajectory in at most n=5 toppling steps:
| In[6]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexStyle -> {5 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 7 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 3 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 1 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 8 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 2 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 6 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 4 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941], 9 -> RGBColor[
0.9363861336280548, 0.5065369688712918, 0.9811065055712941]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 1.}, 0.25]}, InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 2.}, 0.25]}, InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{1., 3.}, 0.25]}, InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 1.}, 0.25]}, InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 2.}, 0.25]}, InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{2., 3.}, 0.25]}, InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 1.}, 0.25]}, InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 2.}, 0.25]}, InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {
{RGBColor[0.9363861336280548, 0.5065369688712918, 0.9811065055712941],
DiskBox[{3., 3.}, 0.25]}, InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\), {"Stabilize", 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/03968d617882c3b2.png) |
| Out[6]= |  |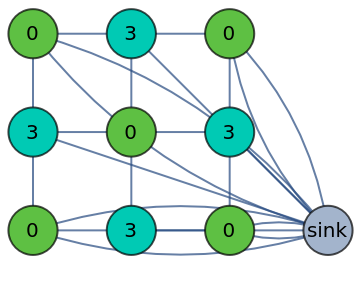
Scope (9)
Grid Graph Sandpiles (3)
Compute the fixed point of the toppling trajectory of an Abelian sandpile on a rectangular grid:
| In[7]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/724be693-70a3-4b32-ac8a-338da468a4ad"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/14e213b85c667dcc.png) |
| Out[7]= |  |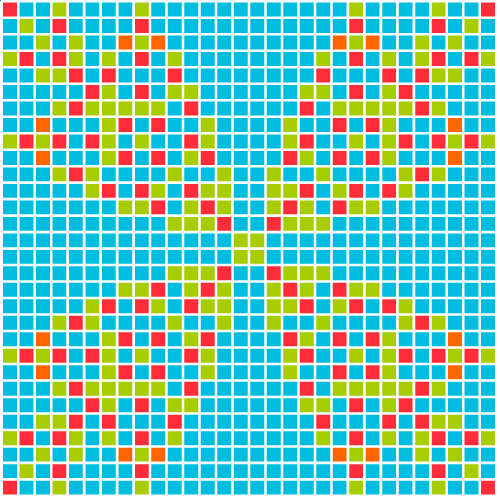
Compute the fixed point of the toppling trajectory on a triangular grid:
| In[8]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/daf89718-ad71-4ffa-8054-b6431a29ed1d"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/2fea84f7008f6537.png) |
| Out[8]= |  |
Compute the fixed point of the toppling trajectory on a hexagonal grid:
| In[9]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a647c3dd-15cc-4ac7-ab1e-034107a4f6f1"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/78c2aa34f35f70a8.png) |
| Out[9]= |  |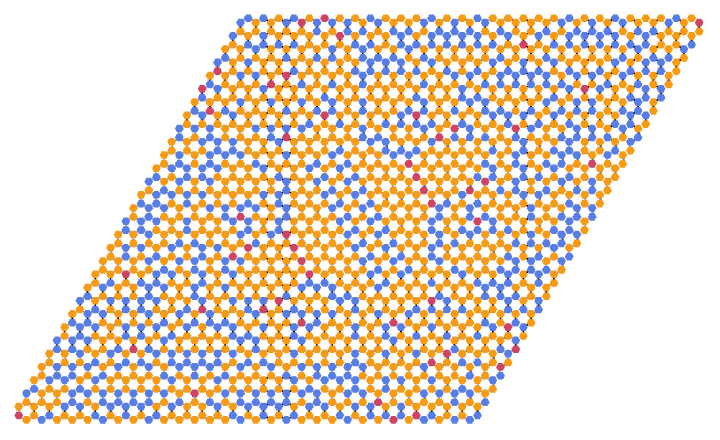
Sandpiles on Fractal Graphs (3)
Compute the fixed point of the toppling trajectory of an Abelian sandpile on a Sierpiński gasket graph:
| In[10]:= | ![ResourceFunction["SandpileTopple"][
Graph[{{0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {0, 7}, {0, 8}, {0, 9}, {0, 10}, {0, 11}, {0, 12}, {0, 13}, {0, 14}, {0, 15}, {0, 16}, {0, 17}, {0, 18}, {0, 19}, {0, 20}, {0, 21}, {0, 22}, {0, 23}, {0, 24}, {0, 25}, {0, 26}, {0, 27}, {0, 28}, {0, 29}, {0, 30}, {0, 31}, {0, 32}, {0, 33}, {0, 34}, {0, 35}, {0, 36}, {0, 37}, {0, 38}, {0, 39}, {0, 40}, {0, 41}, {0, 42}, {0, 43}, {0, 44}, {0, 45}, {0, 46}, {0, 47}, {0, 48}, {0, 49}, {0, 50}, {0, 51}, {0, 52}, {0, 53}, {0, 54}, {0, 55}, {0, 56}, {0, 57}, {0, 58}, {0, 59}, {0, 60}, {0, 61}, {0, 62}, {0, 63}, {0, 64}, {0, 65}, {0, 66}, {0, 67}, {0, 68}, {0, 69}, {0, 70}, {0, 71}, {0, 72}, {0, 73}, {0, 74}, {0, 75}, {0, 76}, {0, 77}, {0, 78}, {0, 79}, {0, 80}, {0, 81}, {0, 82}, {0, 83}, {0, 84}, {0, 85}, {0, 86}, {0, 87}, {0, 88}, {0, 89}, {0, 90}, {0, 91}, {0, 92}, {0, 93}, {0, 94}, {0, 95}, {0, 96}, {0, 97}, {0, 98}, {0, 99}, {0, 100}, {0, 101}, {0, 102}, {0, 103}, {0, 104}, {0, 105}, {
0, 106}, {0, 107}, {0, 108}, {0, 109}, {0, 110}, {0, 111}, {0, 112}, {0, 113}, {0, 114}, {0, 115}, {0, 116}, {0, 117}, {0, 118}, {0, 119}, {0, 120}, {0, 121}, {0, 122}, {0, 123}, {0, 124}, {0, 125}, {0, 126}, {0, 127}, {0, 128}, {0, 129}, {0, 130}, {0, 131}, {0, 132}, {0, 133}, {0, 134}, {0, 135}, {0, 136}, {0, 137}, {0, 138}, {0, 139}, {0, 140}, {0, 141}, {0, 142}, {0, 143}, {0, 144}, {0, 145}, {0, 146}, {0, 147}, {0, 148}, {0, 149}, {0, 150}, {0, 151}, {0, 152}, {0, 153}, {0, 154}, {0, 155}, {0, 156}, {0, 157}, {0, 158}, {0, 159}, {0, 160}, {0, 161}, {0, 162}, {0, 163}, {0, 164}, {0, 165}, {0, 166}, {0, 167}, {0, 168}, {0, 169}, {0, 170}, {0, 171}, {0, 172}, {0, 173}, {0, 174}, {0, 175}, {0, 176}, {0, 177}, {0, 178}, {0, 179}, {0, 180}, {0, 181}, {0, 182}, {0, 183}, {0, 184}, {0, 185}, {0, 186}, {0, 187}, {0, 188}, {0, 189}, {0, 190}, {0, 191}, {0, 192}, {0, 193}, {0, 194}, {0, 195}, {0, 196}, {0, 197}, {0, 198}, {0, 199}, {0, 200}, {0, 201}, {0, 202}, {0, 203}, {0, 204}, {0, 205}, {0, 206}, {0, 207}, {0, 208}, {0, 209}, {0, 210}, {0, 211}, {0, 212}, {0, 213}, {0, 214}, {0, 215}, {0, 216}, {0, 217}, {0, 218}, {0, 219}, {0, 220}, {0, 221}, {0, 222}, {0, 223}, {0, 224}, {0, 225}, {0, 226}, {0, 227}, {0, 228}, {0, 229}, {0, 230}, {0, 231}, {0, 232}, {0, 233}, {0, 234}, {0, 235}, {0, 236}, {0, 237}, {0, 238}, {0, 239}, {0, 240}, {0, 241}, {0, 242}, {0, 243}, {0, 244}, {0, 245}, {0, 246}, {0, 247}, {0, 248}, {0, 249}, {0, 250}, {0, 251}, {0, 252}, {0, 253}, {0, 254}, {0, 255}, {0, 256}, {0, 257}, {0, 258}, {0, 259}, {0, 260}, {0, 261}, {0, 262}, {0, 263}, {0, 264}, {0, 265}, {0, 266}, {0, 267}, {0, 268}, {0, 269}, {0, 270}, {0, 271}, {0, 272}, {0, 273}, {0, 274}, {0, 275}, {0, 276}, {0, 277}, {0, 278}, {0, 279}, {0, 280}, {0, 281}, {0, 282}, {0, 283}, {0, 284}, {0, 285}, {0, 286}, {0, 287}, {0, 288}, {0, 289}, {0, 290}, {0, 291}, {0, 292}, {0, 293}, {0, 294}, {0, 295}, {0, 296}, {0, 297}, {0, 298}, {0, 299}, {0, 300}, {0, 301}, {0, 302}, {0, 303}, {0, 304}, {0, 305}, {0, 306}, {0, 307}, {0, 308}, {0, 309}, {0, 310}, {0, 311}, {0, 312}, {0, 313}, {0, 314}, {0, 315}, {0, 316}, {0, 317}, {0, 318}, {0, 319}, {0, 320}, {0, 321}, {0, 322}, {0, 323}, {0, 324}, {0, 325}, {0, 326}, {0, 327}, {0, 328}, {0, 329}, {0, 330}, {0, 331}, {0, 332}, {0, 333}, {0, 334}, {0, 335}, {0, 336}, {0, 337}, {0, 338}, {0, 339}, {0, 340}, {0, 341}, {0, 342}, {0, 343}, {0, 344}, {0, 345}, {0, 346}, {0, 347}, {0, 348}, {0, 349}, {0, 350}, {0, 351}, {0, 352}, {0, 353}, {0, 354}, {0, 355}, {0, 356}, {0, 357}, {0, 358}, {0, 359}, {0, 360}, {0, 361}, {0, 362}, {0, 363}, {0, 364}, {0, 365}, {0, 366}, 0}, {Null, SparseArray[
Automatic, {367, 367}, 0, {1, {CompressedData["
1:eJxN0nlsD3YYB+AfNZlpsJkhSBFmzdxHgxSpuKo065qWLWiUxV1krjiCqSuu
ippV2mzdOltdoZsraEhF41obV4MmBMFSQdhCSMTT5PuHN+/z+f/N+2mXOfvr
rDqRSGRObZgo6vMhDYmmEZ/wKZ/RnJa0IYa2QQc6EUtnutCNHvSiN3H0J54B
QQJDGEYiIxlFMl+RQipppAffMp4MMpnEd0xjBrPIqr2LeSxgYbCYpSxnBT+Q
zRrWsp5NbCEnyGUHeeRTwM8U8htF7OJPioN9HKCEQxzmKCco5RSnKaOcc5wP
LlHBZa5wjSpucJNq7nCXe8EDHlHDY57wjOe84H9e8ip4w1sifh9FPerzEdE0
ojEf04zmtAhaE0M7OtCRTsTyJZ3pSk960yfoRzwDSWAwQxjGCBJJYjTJQQqp
pDOGbxhPBhPJZDJTmc6MoLbYtb3+nnksYBGLWcIyVrKK7GAdG9hEDlvZxnZ2
8BM7yacgKKSIXRSzm70coIS/OcQRjnOS0uA0ZZylnHNc4BL/UMlVrlMV3KSa
29zhLvd5wEP+pYbHwVOe8x8vecVr3hKpa4niAxrQkOigCU1pRgta0oo2xNCW
9nzOF8QGXehOT/oQR1/6E88ABpHA4GAowxlJEqNJIZU00hnLOCaQEWQymSlM
ZTozyWI2c5nPQhYFS1nOSrJZzVrWs4GNbCaHrUEuP5LHTvL5hV8p4nf+YA/7
2B8c5C8Oc4RjHOckpZziDGcpD85zkQoqucxVrlPFDW5R/Z53HRK2hA==
"], CompressedData["
1:eJxN1nlwjVcYx/F7Y4sQWy0hJIJGUhJbQqKEECkSEkmJlJiIxBKSaFGl08Wg
o0ZXRjvdSNHSaWNCWyWGTksrqkNrLGNrqQ5aWlrG0mnT3+N+35nzx8fze57z
5pwzr3tFVFFFTnmQz+c7oz/8qpbrSYU/UOtLAzSkBksIfag0Z9ZY2ko7cgia
oBnPhpK7yYPO3LSUVjJQHiY/IK3RhmrnhNGHSyfODUN7dGQtnBwjsc7cREpn
mSbF5Cjpgq5Uu280ve3zEPePRnfEsuZV01Pi5AP5kBwvvdCb2lcS6AdIMrN+
MkSGkhOQiCSeHUAeI2OdeTLvc5AMRgrV9k2lT5N0zknFMIxgLY08TnKcuRkp
o2SuPE4eLRnIpNr9suhtn1zum4Vs5LDmVTNeJtjfkz6jUf5AzpOJyKdOkgL6
QiliNllmyixyAaZgKs8WkhfIk87c2OekRKZjBtX2LaUvkwrOKcVslLNWRl4k
i515Be/vCZmH+VS7z0J6+7mnud9CPIXFrHnVPCPP+gLfb6vPyfNYQl0qy+lX
yEpmy+Q1eZ28HC/gRZ5dQV4n6525WSUvyafyGflleQWvUu2c1fRr5U3OXY01
eIO1teQNstGZm7fkbTkr58jvyLt4j2r3raS3fTZx/0q8j42sedXYd3qzbMFH
1I+lir5atjP7RHbKLnIVtmIbz1aTv5UDznw77+9z2YEvqLZvDf0e+ZJzarAb
e1nbQ/5ODjlz85V8Lb/J7+R9sh/fUO1+tfS2z/fctxYHcYg1r5rDckRG6jM5
yh/IP8iPOEo9JifoT8kZZsflgvxCPoGTOM2zp8h/ynVnbuxz8ZP8jPNU2/ci
/SW5wjkX8Ssus3aJ/LfcdOZXeH9X5Rr+oNp9btDbz93ifjfwF26y5lVzW+74
At9nq3flHv6h/it19EF6rr4/MPtPmig39QdyHe7/R8B+//NsELm9dHDmpqE0
knjpRQ6Wxgih2jmh9C2kFeeGohlastaC3EkinLlpLW3s333JI7eVdgij2n3D
6W2fSO4fjo6IYM2rkfxe6SJd0Y0aLTH0PSSOWXfpJwnkGMSiJ8/2IKfKMGce
x/vrLX3Ql2r7JtInyUDOSUR/JLOWRB4h6c7cDJLBMk2KySkyBEOpdr/h9LbP
I9x3ONKQzppXjX2HR0sGMqljJZs+V8Yzy5JJMpmcjXF4lGdzyTNlljM39jmY
KPl4jGr7FtAXShHnFGAKprJWSJ4jZc68iPdVItMxg2r3KaW3nyvnfqWYjTLW
vGr+B3G2NYE=
"]}, CompressedData["
1:eJxTTMoPSmJkYGC4w8TAwMjIxDgywUj098jyMwBqqAVl
"]}]}, {FormatType -> TraditionalForm, ImageSize -> {216.125, Automatic}, GraphLayout -> {"Dimension" -> 2}, VertexCoordinates -> CompressedData["
1:eJxtlz+IFFccx9eAjSSFBBvBwiKQJrEMVg8UG1EJBsQuRJMyiKCINl6hjTZn
k8bGKogWXrEJB0o8j+VuOZfL7b/Z3ZnZP/Pm387M7l0IgRAtkic3M/D7bK45
Pvf9/Xm/937v9+aOX7l28YePKpXKtQOVyoff///zREleVs/OXZ7e+fVx/vcV
6E+hP8n5ec5rsF8Fv4J/FbyKeCs5v1RF/qWTp75069XSX/IK/HeQvwHeRv46
9C3oDcSvwX4d9hvgGvzrqG8L9WyA6wv7vc9vVbG/R06ff/hcFXWsg1fzeLXS
X3INXFXpia+aH198g/N5WeaT+hr0Deg16OvQJ9jPEXiM/XShD6GPsF992Nvg
AfwdsI14LuoZ4rwcsAv/FvI3ka8DvQ29hXgW7Huw74It+HdQTxvr74I7C/sr
+3GA/uuBbfRbH2yBHfSLjfUOoPehd6Fb0HvQd3LdyXlbjTdbJz99P1DFeUlu
5PX1S3/JLXA9r6845y119rdN9/Q9q4wn9W3oO9A74DbsW9Cb0NeVunT1zNkv
fsd9fVvy/v40y/st7euw31C/VF/dvfFJu6xPch3xGuAdxGuAt5F/C9wDW/C3
kK8L+w7su1h/G9xBvNYCy3hN5GuD/8B93pO8tIf7vAt9F/oe7usM8efwn0n/
pTnizRFvV94nk1/MC+Mv58cu/KdYT4L1TJE/hZ5ATxA/g32G+lL4Z/BPUV+C
+lLUly7stzh/s79iHpr1yPk4x/ybgTPJZn/l/JpjvTPoM+gp9Ax6Bt3Dfk6w
fxq6B93D/gQ4fx/+Ps5LI56PeBrr93BeGuel4R8jf4x8EfQIeox4IewD1BPC
P4R/hHoi1BOinmhhf2X/+ei/AP3no98CcIj+0+gPH+v1oQfQQ+gh9AB6MQ/y
99nMB/Eem/OS73OC93cKjsGpfC/NfZfvZQJ9Cn2K9zaCfQT7GHosdXP/5PuQ
yfOsZPK9MfdZ2qc4/1S+X6Y++Z6leL8S8BT5E8SfyvwmvuQA6wsRL0Q9Iewj
5AtRT4R6Iqw/XmAZL8Z6I+Qv5l3xrozVmQdHDm/283fJzEPB5v+R/X5MSn/J
HtjN+7F4F4fqzsHlK98eS8p4Uh9Dn0DXks08lPYe9An04vu8mNMDFb6/d3D5
52Ku2dDtvH+LOenA3oW9o14sHar+/V1c1ivZRbwReIJ4I/AY+YfgQNqbeSV1
H/F8md/MP2mvEU/Lesz+y/o06vEWWMabyHwmnszfVDebw5/09WHOLTkvDe/3
8zjnNuw7sC++b73S/v6Pf/1z+Ubxf3sX3EF8C9xHfAvcw3q64J46euvfS59n
xXfCAGzl998v80m2wV319Z+3n66d0KW/rLcHvQ/dBTuwt6EPoE9Q/wg8Rv0u
9CH0Efbbhv0A9g7Yhv8Q5+uAXWlv5qeMFyN/DPsI9hHsI7l/xl7kN/NfrifC
+kNwgPghvicCuR4TX3Ig+83MC9l/IforAPuSTXzZDyHqDaAH6CcNew17H7oP
3UP9E5yHhu5B97C/Pux97J+Gv49+8HC+GuerS/tvPvveOmDuz6PX7y7cv91S
/wErCwex
"], VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}], "Stabilize",
"DeleteSink" -> True, VertexShape -> Graphics[RegularPolygon[{0, 0}, {1, \[Pi]/2}, 6]], Sequence[VertexSize -> 1.1, ImageSize -> Small]] // Rasterize](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/3eba8ac04bf25544.png) |
| Out[10]= |  |
Compute the fixed point of the toppling trajectory of an Abelian sandpile on a Sierpiński Carpet:
| In[11]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/617f4fce-2adf-483d-9e87-1415340025fa"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/38f77d511f17f047.png) |
| Out[11]= |  |
Compute steps of a toppling trajectory on a 3-ary tree:
| In[12]:= | ![ResourceFunction[
"SandpileTopple"][Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112,
113, 114, 115, 116, 117, 118, 119, 120, 121, 0}, {Null,
SparseArray[
Automatic, {122, 122}, 0, {1, {{0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104, 108, 112, 116,
120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174,
175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199,
200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224,
225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242}, {{2}, {3}, {4}, {122}, {1}, {
5}, {6}, {7}, {1}, {8}, {9}, {10}, {1}, {11}, {12}, {13}, {2}, {
14}, {15}, {16}, {2}, {17}, {18}, {19}, {2}, {20}, {21}, {22}, {
3}, {23}, {24}, {25}, {3}, {26}, {27}, {28}, {3}, {29}, {30}, {
31}, {4}, {32}, {33}, {34}, {4}, {35}, {36}, {37}, {4}, {38}, {
39}, {40}, {5}, {41}, {42}, {43}, {5}, {44}, {45}, {46}, {5}, {
47}, {48}, {49}, {6}, {50}, {51}, {52}, {6}, {53}, {54}, {55}, {
6}, {56}, {57}, {58}, {7}, {59}, {60}, {61}, {7}, {62}, {63}, {
64}, {7}, {65}, {66}, {67}, {8}, {68}, {69}, {70}, {8}, {71}, {
72}, {73}, {8}, {74}, {75}, {76}, {9}, {77}, {78}, {79}, {9}, {
80}, {81}, {82}, {9}, {83}, {84}, {85}, {10}, {86}, {87}, {
88}, {10}, {89}, {90}, {91}, {10}, {92}, {93}, {94}, {11}, {
95}, {96}, {97}, {11}, {98}, {99}, {100}, {11}, {101}, {102}, {
103}, {12}, {104}, {105}, {106}, {12}, {107}, {108}, {109}, {
12}, {110}, {111}, {112}, {13}, {113}, {114}, {115}, {13}, {
116}, {117}, {118}, {13}, {119}, {120}, {121}, {14}, {14}, {
14}, {15}, {15}, {15}, {16}, {16}, {16}, {17}, {17}, {17}, {
18}, {18}, {18}, {19}, {19}, {19}, {20}, {20}, {20}, {21}, {
21}, {21}, {22}, {22}, {22}, {23}, {23}, {23}, {24}, {24}, {
24}, {25}, {25}, {25}, {26}, {26}, {26}, {27}, {27}, {27}, {
28}, {28}, {28}, {29}, {29}, {29}, {30}, {30}, {30}, {31}, {
31}, {31}, {32}, {32}, {32}, {33}, {33}, {33}, {34}, {34}, {
34}, {35}, {35}, {35}, {36}, {36}, {36}, {37}, {37}, {37}, {
38}, {38}, {38}, {39}, {39}, {39}, {40}, {40}, {40}, {1}}}, Pattern}]}, {FormatType -> TraditionalForm, ImageSize -> {295.77381872626273`, Automatic}, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"RadialEmbedding", "RootVertex" -> 0}}, VertexWeight -> {5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, "sink"}}], 3, "AllSteps", "DeleteSink" -> False, VertexSize -> 1,
ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/3c8d0db2c72e08dc.png) |
| Out[12]= |  |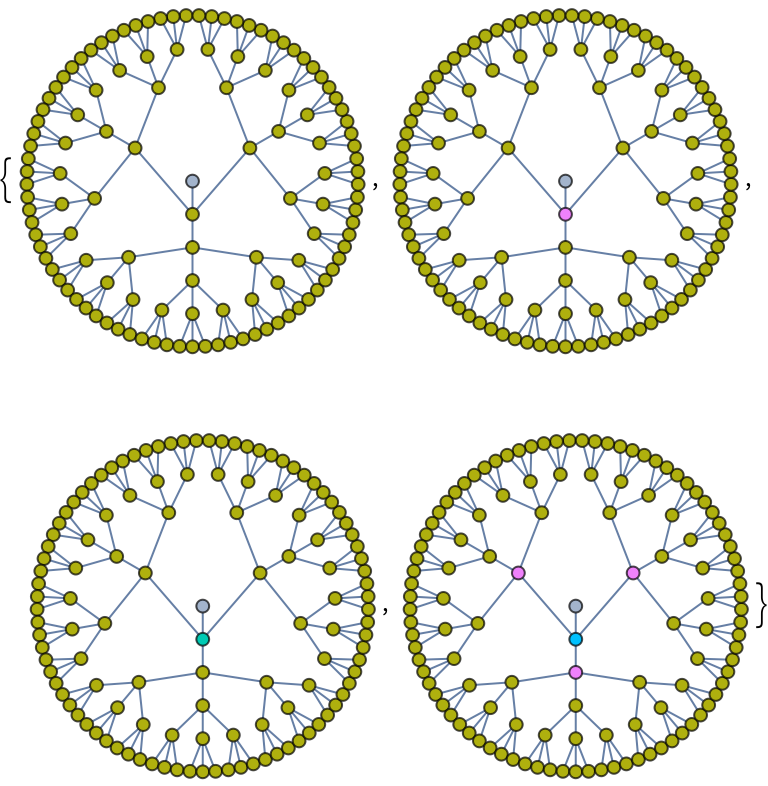
Constructing Sandpile Graphs (3)
Define a function to configure a graph sandpile's boundary conditions by connecting boundary vertices to a sink vertex.
The function below takes the following three arguments: g, the graph to be configured, a list sinkConnections of vertex→number rules specifying the number of connections to the sink for each sink-connected vertex, and sink, which specifies the sink vertex, and defaults to 0:
| In[13]:= | ![ClearAll[connectSink]
connectSink[g_Graph, sinkConnections_List, sink_ : 0] := Graph[
Annotate[{EdgeAdd[g, Flatten[(Table[#1 -> sink, #2] &) @@@ sinkConnections]], sink}, VertexWeight -> "sink"], VertexCoordinates -> Thread[VertexList[g] -> GraphEmbedding[g]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/3abf1d6dd595a4a6.png) |
Configure a valid sandpile by adding and connecting a sink vertex to a graph:
| In[14]:= | ![Module[{dims = {4, 4}, g},
(*Create a rectangular grid graph. Assign it random integer vertex weights in the interval [0,4]*)
g = GridGraph[dims, VertexWeight -> Thread[Range[Times @@ dims] :> RandomInteger[{0, 4}]], Sequence[
ImageSize -> Small, VertexLabels -> "Name"]];
(*Add and connect a sink vertex to the boundary vertices of the grid graph:*)
connectSink[g, Normal[Select[
AssociationThread[VertexList[#] -> (4 - VertexDegree[#])] &@
g, (# != 0 &)]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/0ad6779380ccad41.png) |
| Out[14]= |  |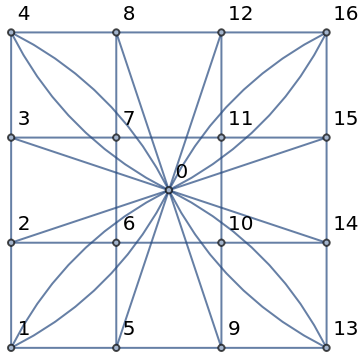
Use an existing vertex as the sink:
| In[15]:= | ![Module[{dims = {3, 3}, g},
(*Create a rectangular grid graph. Assign it random integer vertex weights in the interval [0,4]*)
g = GridGraph[dims, VertexWeight -> Thread[Range[Times @@ dims] :> RandomInteger[{0, 4}]], Sequence[
ImageSize -> Small, VertexLabels -> "Name"]];
(*Add and connect a sink vertex to the boundary vertices of the grid graph:*)
connectSink[g, Normal[Select[
AssociationThread[VertexList[#] -> (4 - VertexDegree[#])] &@
g, (# != 0 &)]], 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/4bea1ef81c522c2f.png) |
| Out[15]= |  |
Options (5)
ColorFunction (1)
When "StyleSandpile" is set to True, set the vertex color scheme using the ColorFunction option:
| In[16]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{1., 1.}, 0.25], InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.25], InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.25], InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.25], InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 2.}, 0.25], InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 3.}, 0.25], InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 1.}, 0.25], InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.25], InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 3.}, 0.25], InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{178.9453125, 140.}]\), ColorFunction -> 24]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/538e12fd45999796.png) |
| Out[16]= |  |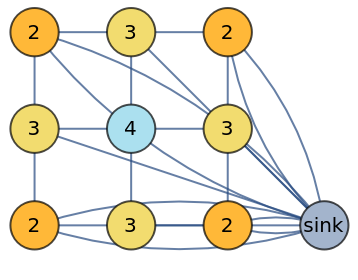
DeleteSink (1)
To delete the sink vertex from computed toppled sandpiles, set the "DeleteSink" option to True:
| In[17]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{1., 1.}, 0.25], InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.25], InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.25], InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.25], InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 2.}, 0.25], InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 3.}, 0.25], InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 1.}, 0.25], InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.25], InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 3.}, 0.25], InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{178.9453125, 140.}]\), "DeleteSink" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/19c61dd3c666bc61.png) |
| Out[17]= |  |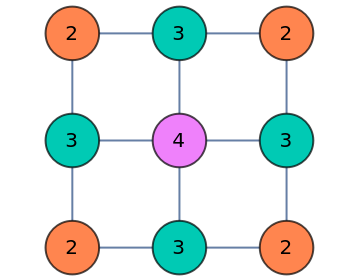
StyleSandpile (1)
By default, SandpileTopple will style toppled sandpiles so that the vertices are colored by their weights. To disable this behavior and preserve the styling of the initial sandpile, set the "StyleSandpile" option to False:
| In[18]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{1., 1.}, 0.25], InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.25], InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.25], InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.25], InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 2.}, 0.25], InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 3.}, 0.25], InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 1.}, 0.25], InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.25], InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 3.}, 0.25], InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{178.9453125, 140.}]\), "StyleSandpile" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/55c5d6f4a48f90ac.png) |
| Out[18]= |  |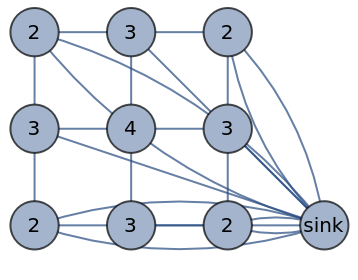
VertexShape (1)
The behaviour of the VertexShape option is modified so as to preserve vertex colors when the shape is specified as a single Graphics object:
| In[19]:= | ![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{1., 1.}, 0.25], InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.25], InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.25], InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.25], InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 2.}, 0.25], InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 3.}, 0.25], InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 1.}, 0.25], InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.25], InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 3.}, 0.25], InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{178.9453125, 140.}]\), VertexShape -> Graphics[Rectangle[]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/2f9b43575d1da715.png) |
| Out[19]= |  |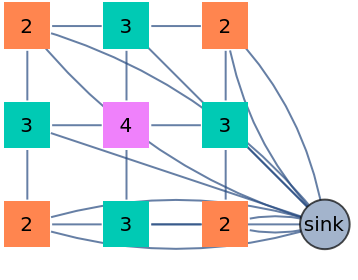
![ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {Null, SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 3, 6, 8, 11, 13, 15, 17, 19, 20, 20}, {{2}, {
4}, {10}, {3}, {5}, {10}, {6}, {10}, {5}, {7}, {10}, {
6}, {8}, {9}, {10}, {8}, {10}, {9}, {10}, {10}}}, {1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2}}]}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2, "VertexLayout" -> {"GridEmbedding", "Dimension" -> {3, 3}}},
ImageSize -> Small, VertexLabels -> {
Placed["VertexWeight", Center]}, VertexSize -> {
Rational[1, 2]}, VertexWeight -> {4, 4, 4, 4, 4, 4, 4, 4, 4, "sink"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1., 1.}, {1., 2.}}, 0.25], ArrowBox[{{1., 1.}, {2., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 1.4933222415493483`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 1.}, {2.499999999999996, 0.5066777584506517}, {4., 1.}}], 0.25], ArrowBox[{{1., 2.}, {1., 3.}}, 0.25], ArrowBox[{{1., 2.}, {2., 2.}}, 0.25], ArrowBox[{{1., 2.}, {4., 1.}}, 0.25], ArrowBox[{{1., 3.}, {2., 3.}}, 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.8288814943662333`, 2.493322241549353}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{1., 3.}, {2.171118505633749, 1.5066777584506628`}, {4., 1.}}], 0.25], ArrowBox[{{2., 1.}, {2., 2.}}, 0.25], ArrowBox[{{2., 1.}, {3., 1.}}, 0.25], ArrowBox[{{2., 1.}, {4., 1.}}, 0.25], ArrowBox[{{2., 2.}, {2., 3.}}, 0.25], ArrowBox[{{2., 2.}, {3., 2.}}, 0.25], ArrowBox[{{2., 3.}, {3., 3.}}, 0.25], ArrowBox[{{2., 3.}, {4., 1.}}, 0.25], ArrowBox[{{3., 1.}, {3., 2.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999949, 1.1644407471831046`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 1.}, {3.499999999999994, 0.8355592528168789}, {4., 1.}}], 0.25], ArrowBox[{{3., 2.}, {3., 3.}}, 0.25], ArrowBox[{{3., 2.}, {4., 1.}}, 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.828881494366222, 2.1644407471831513`}, {4., 1.}}], 0.25], ArrowBox[
BezierCurveBox[{{3., 3.}, {3.1711185056337494`, 1.8355592528168931`}, {4., 1.}}], 0.25]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{1., 1.}, 0.25], InsetBox["4", {1., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.25], InsetBox["4", {1., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.25], InsetBox["4", {1., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.25], InsetBox["4", {2., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 2.}, 0.25], InsetBox["4", {2., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{2., 3.}, 0.25], InsetBox["4", {2., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 1.}, 0.25], InsetBox["4", {3., 1.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.25], InsetBox["4", {3., 2.},
BaseStyle->"Graphics"]}, {DiskBox[{3., 3.}, 0.25], InsetBox["4", {3., 3.},
BaseStyle->"Graphics"]}, {DiskBox[{4., 1.}, 0.25], InsetBox["\<\"sink\"\>", {4., 1.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{178.9453125, 140.}]\),
EdgeStyle -> Directive[Thick, Dashed, Lighter[Blue]],
VertexStyle -> {1 -> Darker[Cyan, .2], 9 -> Darker[Green, .2]},
VertexLabels -> Placed[Automatic, Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/7e235119da5554bd.png)
Possible Issues (1)
SandpileTopple may not terminate if the sink vertex of the provided sandpile is not connected to at least one non-sink vertex:
| In[21]:= | ![TimeConstrained[ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 2}, {Null, {{2, 3}, {3, 2}}}, {ImageSize -> Small, VertexLabels -> {"VertexWeight"}, VertexWeight -> {"sink", 1, 2}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[
BezierCurveBox[{{1.06251, -0.06251}, {
0.5625100000000007, -0.22695074718311647`}, {
0.06251000000000007, -0.06251}}], 0.01273], ArrowBox[
BezierCurveBox[{{1.06251, -0.06251}, {0.5625100000000007, 0.10193074718311639`}, {0.06251000000000007, -0.06251}}],
0.01273]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.06251, -0.18752999999999997`}, 0.01273], InsetBox["\<\"sink\"\>", Offset[{2, 2}, {0.07524, -0.17479999999999998}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1.06251, -0.06251}, 0.01273], InsetBox["1", Offset[{2, 2}, {1.07524, -0.04978}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.06251000000000007, -0.06251}, 0.01273], InsetBox["2", Offset[{2, 2}, {0.07524000000000007, -0.04978}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->Small]\), "Stabilize", Sequence[
ImageSize -> Small, VertexLabels -> "VertexWeight"]], 1]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/009dd00b0035189b.png) |
| Out[21]= |  |
Neat Examples (2)
Animate a toppling trajectory on a fully unstable scale-free graph sandpile:
| In[22]:= | ![ListAnimate[ResourceFunction["SandpileTopple"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 0}, {Null, SparseArray[
Automatic, {101, 101}, 0, {1, {{0, 20, 45, 59, 70, 75, 79, 79, 85, 94, 101, 101, 108, 110, 116, 121, 125, 133, 134, 136, 138, 138, 139, 140, 141, 149, 151, 153, 153, 159, 160, 160, 161, 163, 167, 168, 168, 170, 172, 174, 174, 174, 176, 178, 178, 178, 179, 179, 180, 180, 182, 183, 184, 184, 184, 185, 185, 185, 185, 185, 185, 185, 185, 188, 188, 188, 188, 189, 189, 189, 190, 190, 190, 191, 192, 192, 192, 193, 193, 193, 195, 195, 195, 196, 197, 197, 197, 197, 197, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198}, {{2}, {3}, {5}, {7}, {8}, {9}, {10}, {12}, {
17}, {22}, {26}, {28}, {30}, {32}, {37}, {41}, {65}, {
85}, {99}, {101}, {3}, {4}, {5}, {6}, {7}, {8}, {9}, {
11}, {13}, {15}, {20}, {21}, {23}, {27}, {30}, {34}, {
37}, {38}, {44}, {46}, {50}, {54}, {74}, {76}, {87}, {
4}, {12}, {16}, {23}, {24}, {26}, {48}, {51}, {56}, {
62}, {70}, {78}, {79}, {91}, {6}, {10}, {14}, {17}, {
38}, {42}, {64}, {84}, {86}, {88}, {93}, {11}, {19}, {
24}, {45}, {100}, {16}, {25}, {31}, {39}, {22}, {27}, {
61}, {64}, {97}, {99}, {14}, {36}, {40}, {45}, {46}, {
63}, {65}, {75}, {76}, {18}, {19}, {25}, {29}, {33}, {
60}, {68}, {13}, {18}, {21}, {43}, {58}, {59}, {94}, {
47}, {58}, {15}, {31}, {32}, {39}, {67}, {83}, {35}, {
40}, {74}, {87}, {91}, {34}, {47}, {50}, {90}, {28}, {
33}, {61}, {69}, {70}, {78}, {83}, {89}, {20}, {63}, {
67}, {49}, {97}, {29}, {92}, {52}, {36}, {52}, {53}, {
54}, {55}, {60}, {71}, {84}, {72}, {95}, {62}, {81}, {
43}, {57}, {66}, {68}, {90}, {96}, {57}, {72}, {41}, {
98}, {35}, {55}, {69}, {73}, {85}, {53}, {79}, {42}, {
49}, {44}, {86}, {48}, {80}, {66}, {77}, {59}, {92}, {
51}, {94}, {56}, {75}, {73}, {80}, {88}, {89}, {77}, {
71}, {82}, {95}, {93}, {81}, {82}, {98}, {96}, {100}}}, {
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}]}, {GraphLayout -> {"Dimension" -> 2}, VertexWeight -> {20, 27, 17, 14, 8, 7, 3, 9, 12, 10, 3, 10, 5, 9, 8, 7, 11, 4, 5, 5, 3, 4, 4, 4, 11, 5, 5, 3, 9, 4, 3,
4, 5, 7, 4, 3, 5, 5, 5, 3, 3, 5, 5, 3, 3, 4, 3, 4, 3, 5, 4, 4, 3, 3, 4, 3, 3, 3, 3, 3, 3, 3, 6, 3, 3, 3, 4, 3, 3, 4, 3, 3, 4, 4, 3, 3, 4, 3, 3, 5, 3, 3, 4, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, "sink"}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJw1VHs41Pke/jXX38yYmZ9rT21sYsd0KstErdnq+2FDdMK2uy6H2JNctpKh
spEusm0uScq1lUxWKKxUbp1oC6eNEOPeTcjIZWZkBmNwnOc5532e93n/fZ/n
vRjvD90bQMIwLGCZ/9VtIx62lnNkoGd1rb05TQWW953CnzASTJvL3azjcWj+
gE/FxajRD1InntUcDYQb3m1ONadDZ1jlyo4MDPTo77caLjDhx0KG8uALMkzZ
F52760qDJLZEXkCmQ67e+UcPA5bQkLml9fq7TPgjPwF255EhLsTmBLlmAWXP
rRGW1TLAT1/H1VOFw5pdwtNR/RzoVsR/xcgmge+qQeJODg6HBCUkbNlP0Dsf
fsoNGsx+6Vg7SibAWvTNYW8fMkhtL1UWNmuDQWBTRmkjDapLfSud91FBek0/
1alAjb7XOVSZXcaE2O1B8n59EnCIHTvtTmnBxoudirAUKuRXYk0J6Sqk+6+0
tCv7mTAVbSG0XEMHCVesza/lgjBysM9v8yIq3KhjcSGXAv4LidXgtIR43YfL
r7uSoDzynyfdewnosSdWsgdZ0GXtX/mQQQXnx4JKWtM4WtxjzI6T0cAkIF+r
o4kGnaObwl5649D/ID15TR4LSFdbRhMaMRC8auxT0qYQL/7SpoLTTKiv/DAg
9VIh02fmRJvtIroeMXDIbBcJRizYJ0Juz6HnmWLftWptmJXGB/zizgR9cLO9
Fc4EKbkrn2XIBmkpu1jRioNRV5bGRsiCqoB91RRMjQL7z4/0bsXh6SPLpAE+
B+qLX5y/UP4JCZ/UvGd+O484W83Gi99h0IeRVVUv5MjpDTqZyqPC0RAfWZUp
AdQjzvomf1IBL16bRiqbRxmJ4t2ZhRSoG/pFdMIFg/aPT3oYZouItQpWhHmQ
IWSb6eq6zUzoy86lpx8gg9HO8gtf3OXAheuxHX79THj+dtjz3/c1iGLOizv5
23Lfrqb53PqoQtrXNGS7ZG1QxdQUtRtxgdlzdC48egntoCZZHt7NhT0jpwY9
XQh45rjjcVw3DqJVxrmbbXBwkNAFjfsIOFgrjkwsXULtg6H2b2Z0QB3lcLto
vRRN6UpFZzkYnH3JD3bei0EDNWziV1cFupQZY4NFaVCfEYfw7SYgytfTvQrk
aNL0og85mwuNr2pvXY7kQJqDJEy9HYeS+k56eyAFvG2Glw6UrIDHFQeCfxbg
YGJbpsx6S4bCo1vwTiYJTnNGeInBSsSnZAyzvxtCkmlFe/jnbPhzMqvVJUwb
1vHH83bFEAA5Ep1eExq4NYgX8vbqQWNMy+X6egas62hL3harCwK/QJbJS22Q
qIoSxlkapBORlXLxKwq0j13uvSf6gORsrdao8BEk07Bfh/JJgCbsArIzcMCu
im8anptBG3GzaNd4Gpgxjgx8KlMgPVnLUcopHLx4srbfFrWAt6N2yK9GD24n
uchnn3KB0OuT3ZcRMNl2sIBTQIE4kuwY964uvO6xcHYtpkL0tRleXN88Gtf5
4Y/0egVaaVEl/rsRCQzez5a0emiQoH/iVPgNBjwhpT762kqJHmsicgLn36Bc
1cVvjR2ZoFTc7zh3T4USTC26/IvG0NZ0Yeze/Cl09gnT0lmHAzmOOYlDZwio
CDWJcujUgtmw8r9sg2hQf8ZLdBU48I/ZgsjnN3Qhfmb0irQZh0ytB1sYUjV6
tYfT2/ilBu10HxHeezCKjA0arCZVFKCPaSf/TaNB2U2/WrqXDCLn3/2OGxbJ
kJtsym9FyyiqcyJXfJP5CWH/wyPTMcc0NQuG/asEzkVKtN8Ek3stLeeUYigq
Oba8D3bSAeaEEuk9y/ixzZwCbq+eGp9rIIFb4xVdzygKuOTRXnMlM2hpPN59
Sc2Bg5bHnYYGGXDtTAnzyIZJdLn6M6x/+S9ulc7cSPaQIjHuZ1AxpgUGE6mx
q9u40OeNDndrPqKH3dMNdyRM+L+vXW3oc483JHhPFFZsES33YXfEQMKD5d9W
xQTJDUkQ4V/R+lezLmSybraHWvWg+aoMMZ9OAF8ZuG5DtR5sT6q1HkuiwHe9
Axx9MRnqat8uVAjk6PtLxUHPUwjARUX26xUDKDBh2M2rZQnNHQuuC/FYAc3B
5fb2mwg4bvV7td27aeQwGX16bvUCGqz5ws6OzYb/AOg10nc=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[CompressedData["
1:eJwVxVtbAUEYAGDfN7PbzjR2dxCGVnaFQhJK51VKERI60Fl13b/sd1UX7/O6
8+/RHAOBwM+f/wGBgAYLYAADDgIkRCEBy5CCNGRhHU7gFj7gCwlS1FDHBTSQ
4SIG0cIILmEMk5hCD7OYwxKWsYo72MUe3hNKBLFJjMRJglRIjeySY9ImA3JN
HqlOOTWppDlaoE06oXf0gT5ri1pYi2sb2qdu60pf0fNG1EgaR0bTeDc+mMlW
2RrbYGXmsxN2xXo8xMNccYe7/JCfiaAIiSVRFPviQLwEN4P7pmWumGkzb7bM
sZWx1qyudW892p69aVftmVyWrjyS57ItB3Isp6FI2A+3IluR96gTe4rX1aqq
q221oxrqUF2oSeIy8Zo8Tt44RWfPOXXOnJnzltpLX7rr7tzLeA3v3OtkbrPb
2etcIbeVL+XvCpXCsHha7JcPKk/VWvWltlu/anT8of/gT1v99kVn1H3tPw9v
hqPxfPI2/fwF5E04Ew==
"], 0.04407905312192746]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.04407905312192746], DiskBox[2, 0.04407905312192746], DiskBox[3, 0.04407905312192746], DiskBox[4, 0.04407905312192746], DiskBox[5, 0.04407905312192746], DiskBox[6, 0.04407905312192746], DiskBox[7, 0.04407905312192746], DiskBox[8, 0.04407905312192746], DiskBox[9, 0.04407905312192746], DiskBox[10, 0.04407905312192746], DiskBox[11, 0.04407905312192746], DiskBox[12, 0.04407905312192746], DiskBox[13, 0.04407905312192746], DiskBox[14, 0.04407905312192746], DiskBox[15, 0.04407905312192746], DiskBox[16, 0.04407905312192746], DiskBox[17, 0.04407905312192746], DiskBox[18, 0.04407905312192746], DiskBox[19, 0.04407905312192746], DiskBox[20, 0.04407905312192746], DiskBox[21, 0.04407905312192746], DiskBox[22, 0.04407905312192746], DiskBox[23, 0.04407905312192746], DiskBox[24, 0.04407905312192746], DiskBox[25, 0.04407905312192746], DiskBox[26, 0.04407905312192746], DiskBox[27, 0.04407905312192746], DiskBox[28, 0.04407905312192746], DiskBox[29, 0.04407905312192746], DiskBox[30, 0.04407905312192746], DiskBox[31, 0.04407905312192746], DiskBox[32, 0.04407905312192746], DiskBox[33, 0.04407905312192746], DiskBox[34, 0.04407905312192746], DiskBox[35, 0.04407905312192746], DiskBox[36, 0.04407905312192746], DiskBox[37, 0.04407905312192746], DiskBox[38, 0.04407905312192746], DiskBox[39, 0.04407905312192746], DiskBox[40, 0.04407905312192746], DiskBox[41, 0.04407905312192746], DiskBox[42, 0.04407905312192746], DiskBox[43, 0.04407905312192746], DiskBox[44, 0.04407905312192746], DiskBox[45, 0.04407905312192746], DiskBox[46, 0.04407905312192746], DiskBox[47, 0.04407905312192746], DiskBox[48, 0.04407905312192746], DiskBox[49, 0.04407905312192746], DiskBox[50, 0.04407905312192746], DiskBox[51, 0.04407905312192746], DiskBox[52, 0.04407905312192746], DiskBox[53, 0.04407905312192746], DiskBox[54, 0.04407905312192746], DiskBox[55, 0.04407905312192746], DiskBox[56, 0.04407905312192746], DiskBox[57, 0.04407905312192746], DiskBox[58, 0.04407905312192746], DiskBox[59, 0.04407905312192746], DiskBox[60, 0.04407905312192746], DiskBox[61, 0.04407905312192746], DiskBox[62, 0.04407905312192746], DiskBox[63, 0.04407905312192746], DiskBox[64, 0.04407905312192746], DiskBox[65, 0.04407905312192746], DiskBox[66, 0.04407905312192746], DiskBox[67, 0.04407905312192746], DiskBox[68, 0.04407905312192746], DiskBox[69, 0.04407905312192746], DiskBox[70, 0.04407905312192746], DiskBox[71, 0.04407905312192746], DiskBox[72, 0.04407905312192746], DiskBox[73, 0.04407905312192746], DiskBox[74, 0.04407905312192746], DiskBox[75, 0.04407905312192746], DiskBox[76, 0.04407905312192746], DiskBox[77, 0.04407905312192746], DiskBox[78, 0.04407905312192746], DiskBox[79, 0.04407905312192746], DiskBox[80, 0.04407905312192746], DiskBox[81, 0.04407905312192746], DiskBox[82, 0.04407905312192746], DiskBox[83, 0.04407905312192746], DiskBox[84, 0.04407905312192746], DiskBox[85, 0.04407905312192746], DiskBox[86, 0.04407905312192746], DiskBox[87, 0.04407905312192746], DiskBox[88, 0.04407905312192746], DiskBox[89, 0.04407905312192746], DiskBox[90, 0.04407905312192746], DiskBox[91, 0.04407905312192746], DiskBox[92, 0.04407905312192746], DiskBox[93, 0.04407905312192746], DiskBox[94, 0.04407905312192746], DiskBox[95, 0.04407905312192746], DiskBox[96, 0.04407905312192746], DiskBox[97, 0.04407905312192746], DiskBox[98, 0.04407905312192746], DiskBox[99, 0.04407905312192746], DiskBox[100, 0.04407905312192746], DiskBox[101, 0.04407905312192746]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\), 40, "AllSteps", VertexSize -> 1], AnimationRunning -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/0bf5e10d5737c1bd.png) |
| Out[22]= |  |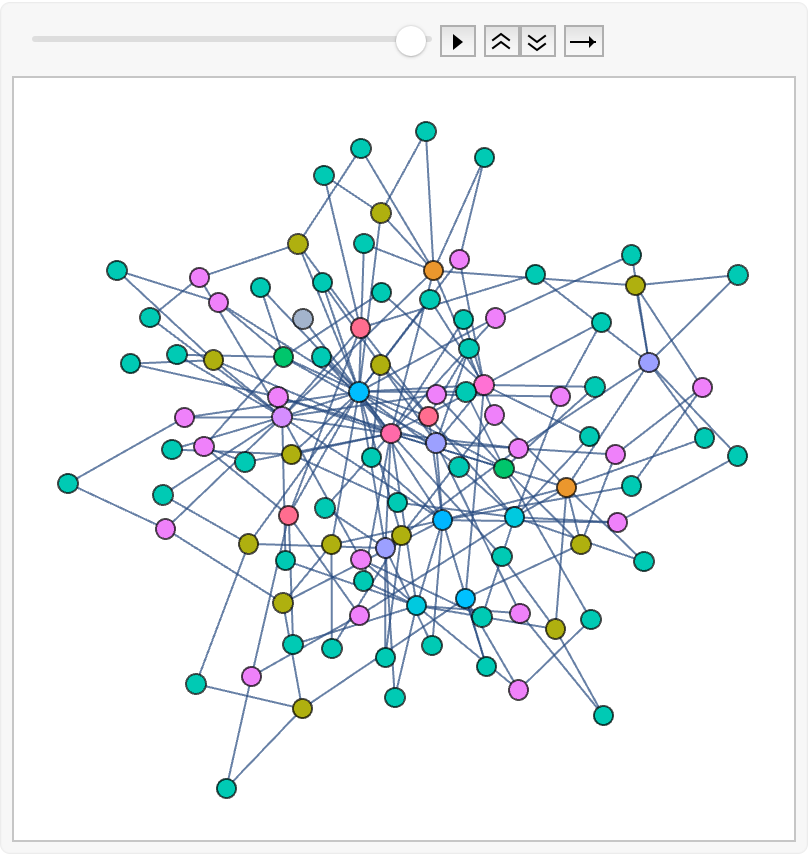
Topple arbitrary mesh graphs such as this grounded triceratops:
| In[23]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bd15104b-4b57-43e8-8e2a-c0651afa0569"]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/76e0f0cd4ac22d5b.png){kind=small} |
| Out[24]= |  |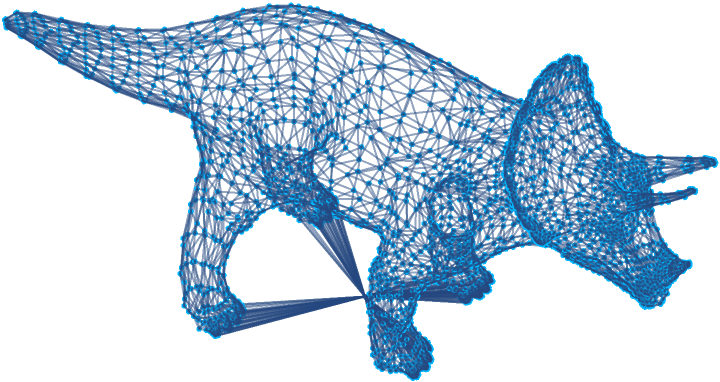
| In[25]:= | ![Timing[Rasterize@
ResourceFunction["SandpileTopple"][triceratopsSandpile, "Stabilize",
VertexSize -> 10]]](https://www.wolframcloud.com/obj/resourcesystem/images/a2a/a2af7ed5-f252-4242-abf7-8aa9d00ea312/4e459c9f69eaa8d2.png){kind=small} |
| Out[25]= |  |
Publisher
Related Links
- An Elementary Introduction to the Wolfram Language: Graphs and Networks
- Wolfram Documentation: Graph Construction and Representation
Requirements
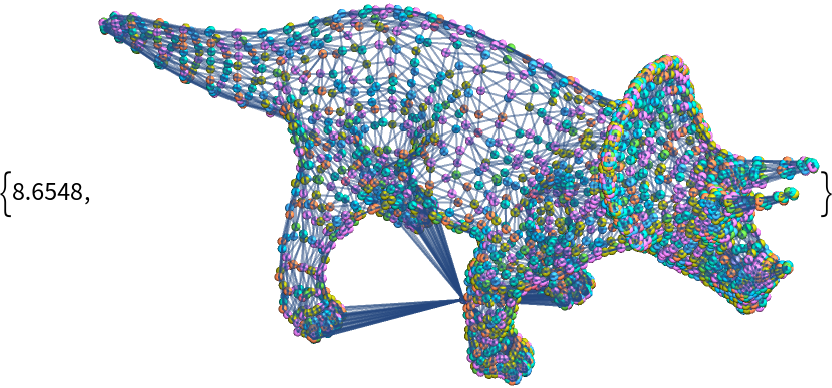Wolfram Language 13.0 (December 2021) or above
Version History
- 1.0.0 – 05 February 2024
Source Metadata
Related Symbols
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License