Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SameExpressionShapeQ

Source Notebook

Check if expressions have the same shape

Contributed by: Richard Hennigan (Wolfram Research)

ResourceFunction["SameExpressionShapeQ"][expr1,…,exprn]

yields True if all the expri have the same shape and yields False otherwise.

Details and Options

Two expressions expr1 and expr2 are defined to have the same shape when, for any valid position specification p1,…,pn, the subexpression expr1[[p1,…,pn]] exists if and only if the subexpression expr2[[p1,…,pn]] exists.

Examples

Basic Examples (1) 

Check if expressions have the same shape:

In[1]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y]]
Out[1]=
In[2]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y, z]]
Out[2]=
In[3]:=
ResourceFunction["SameExpressionShapeQ"][a + b + f[x], {1, 2, {3}}]
Out[3]=
In[4]:=
ResourceFunction["SameExpressionShapeQ"][a + b + f[{x}], {1, 2, {3}}]
Out[4]=
In[5]:=
ResourceFunction["SameExpressionShapeQ"][f[x], h[g][y]]
Out[5]=

Scope (5) 

Associations must agree on keys:

In[6]:=
ResourceFunction["SameExpressionShapeQ"][<|a -> f[x]|>, <|a :> {1}|>]
Out[6]=
In[7]:=
ResourceFunction["SameExpressionShapeQ"][<|a -> f[x]|>, <|b :> {1}|>]
Out[7]=

A reordering of keys only changes the shape if the corresponding values have a different shape:

In[8]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> f[1], b -> 2, c -> g[3]|>, <|c -> {z}, b -> y, a -> {x}|>]
Out[8]=
In[9]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> 1, b -> {}|>, <|b -> {}, a -> 1|>]
Out[9]=

Compare expressions without evaluation:

In[10]:=
ResourceFunction["SameExpressionShapeQ"][Unevaluated[Echo[1]], Unevaluated[Print[x]]]
Out[10]=
In[11]:=
ResourceFunction["SameExpressionShapeQ"][Unevaluated[Echo[1]], Unevaluated[1 + 1]]
Out[11]=

The Unevaluated wrapper is not considered part of the expression:

In[12]:=
ResourceFunction["SameExpressionShapeQ"][Unevaluated[Echo[1]], f[x]]
Out[12]=

Any number of arguments can be given:

In[13]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y], h[z]]
Out[13]=
In[14]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y, y], h[z]]
Out[14]=

Applications (4) 

Check if ragged arrays have compatible dimensions:

In[15]:=
list1 = Table[RandomInteger[5, i], {i, 5}]
Out[15]=
In[16]:=
list2 = NestList[Append[#, RandomInteger[5]] &, {RandomInteger[5]}, 4]
Out[16]=
In[17]:=
list3 = Table[RandomInteger[5, i], {i, 0, 4}]
Out[17]=

These are compatible:

In[18]:=
ResourceFunction["SameExpressionShapeQ"][list1, list2]
Out[18]=
In[19]:=
list1 + list2
Out[19]=

These are not:

In[20]:=
ResourceFunction["SameExpressionShapeQ"][list1, list3]
Out[20]=

Attempting to add them results in an error:

In[21]:=
list1 + list3
Out[21]=

Properties and Relations (6) 

An expression is always the same shape as itself, so SameExpressionShapeQ is always true for a single argument:

In[22]:=
ResourceFunction["SameExpressionShapeQ"][f[x]]
Out[22]=

SameExpressionShapeQ[] is defined to be True:

In[23]:=
ResourceFunction["SameExpressionShapeQ"][]
Out[23]=

This is consistent with the behavior of SameQ:

In[24]:=
SameQ[]
Out[24]=

For normal expressions, SameExpressionShapeQ[expr1,…,exprn] is effectively equivalent to testing if all the ExpressionGraph[expri] are equivalent under IsomorphicGraphQ:

In[25]:=
expr1 = a + b + f[x]; expr2 = {1, 2, {3}}; expr3 = a + b + f[{x}];
In[26]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr2]
Out[26]=
In[27]:=
IsomorphicGraphQ[ExpressionGraph[expr1], ExpressionGraph[expr2]]
Out[27]=

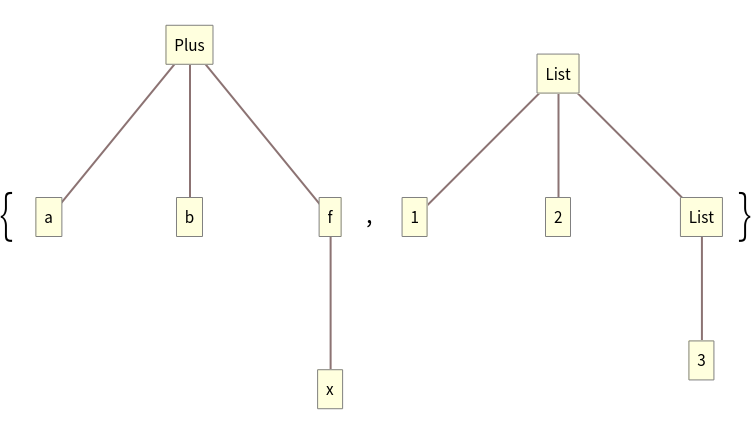
Compare using TreeForm:

In[28]:=
{TreeForm[expr1], TreeForm[expr2]}
Out[28]=

These two have different shapes:

In[29]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr3]
Out[29]=
In[30]:=
IsomorphicGraphQ[ExpressionGraph[expr1], ExpressionGraph[expr3]]
Out[30]=

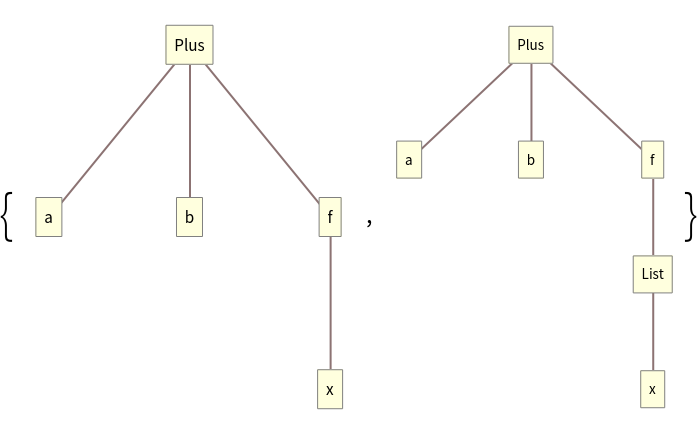
Compare using TreeForm:

In[31]:=
{TreeForm[expr1], TreeForm[expr3]}
Out[31]=

Represent the underlying "shape" of expressions by replacing all atomic values with one identical value:

In[32]:=
expr1 = h[][f[x, g[y, z]]]; expr2 = f[][{1, 2 + x}]; expr3 = f[g[], g[y, z]];
In[33]:=
s1 = Replace[expr1, _ -> 0, {-1}, Heads -> True]
Out[33]=
In[34]:=
s2 = Replace[expr2, _ -> 0, {-1}, Heads -> True]
Out[34]=
In[35]:=
s3 = Replace[expr3, _ -> 0, {-1}, Heads -> True]
Out[35]=

These have the same shape:

In[36]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr2]
Out[36]=
In[37]:=
s1 === s2
Out[37]=

These do not:

In[38]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr3]
Out[38]=
In[39]:=
s1 === s3
Out[39]=

Highlight differences:

In[40]:=
ResourceFunction["ExpressionLineDiff"][s1, s3]
Out[40]=

Another way to understand the shape of a normal expression is by looking at the positions of all subexpressions:

In[41]:=
expr1 = h[][f[x, g[y, z]]]; expr2 = f[][{1, 2 + x}]; expr3 = f[g[], g[y, z]];
In[42]:=
p1 = Position[expr1, _, Heads -> True]
Out[42]=
In[43]:=
p2 = Position[expr2, _, Heads -> True]
Out[43]=
In[44]:=
p3 = Position[expr3, _, Heads -> True]
Out[44]=

When the positions are the same, the expressions have the same shape:

In[45]:=
p1 === p2
Out[45]=
In[46]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr2]
Out[46]=
In[47]:=
p1 === p3
Out[47]=
In[48]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr3]
Out[48]=

For associations to be considered the same shape, their corresponding parts must be the same shape whether indexed by key or numeric position:

In[49]:=
a1 = <|a -> 1, b -> {}, c -> x|>; a2 = <|c -> x, b -> {}, a -> 1|>;

Check subexpressions by key indexing:

In[50]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a2[[i]]], {i, {Key[a], Key[b], Key[c]}}]
Out[50]=

Check subexpressions by their ordinal positions:

In[51]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a2[[i]]], {i, 3}]
Out[51]=

Since both methods of indexing are in agreement, these have the same shape:

In[52]:=
ResourceFunction["SameExpressionShapeQ"][a1, a2]
Out[52]=

Here is another Association that only differs in key order:

In[53]:=
a3 = <|b -> {}, a -> 1, c -> x|>;

Check subexpressions by key indexing:

In[54]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a3[[i]]], {i, {Key[a], Key[b], Key[c]}}]
Out[54]=

Check subexpressions by their ordinal positions:

In[55]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a3[[i]]], {i, 3}]
Out[55]=

It is not considered the same shape, since indexing by numeric position yields incompatible subexpressions:

In[56]:=
ResourceFunction["SameExpressionShapeQ"][a1, a3]
Out[56]=

Possible Issues (2) 

For associations, SameExpressionShapeQ considers keys to be structural positions rather than subexpressions:

In[57]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> x, b -> y|>, <|b -> y, c -> z|>]
Out[57]=
In[58]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> x, b -> y|>, <|a -> 1, b -> 2|>]
Out[58]=

For lists of rules, the keys are normal subexpressions:

In[59]:=
ResourceFunction[ "SameExpressionShapeQ"][{a -> x, b -> y}, {b -> y, c -> z}]
Out[59]=

Version History

  • 1.0.0 – 24 August 2020

Related Resources

License Information