Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SalzerPiessensInversionWeights

Source Notebook

Get a list of abscissas and weights for the numerical inverse Laplace transform

Contributed by: Jan Mangaldan

ResourceFunction["SalzerPiessensInversionWeights"][n]

gives a list of the 2 n+1 triples {xi,wi,εi} of the (2 n+1)-point Salzer-Piessens formula for numerical Laplace transform inversion, where wi and εi are the corresponding weight and error weight of the abscissa xi.

ResourceFunction["SalzerPiessensInversionWeights"][n,prec]

uses the working precision prec.

Details

Salzer-Piessens approximates the inverse Laplace transform as a linear combination of values of the function to be transformed, evaluated at abscissas xi: .
An error estimate of the result can be computed using a similar formula, but using the error weights εi in place of the weights wi: .
The Salzer-Piessens method is based on the roots of the nth order Bessel polynomial comprising n of the abscissas for a Gaussian quadrature rule. An n+1 Kronrod-type extension is then built out of this Gaussian rule.
The error estimate is equivalent to the difference between the complete (2 n+1)-point approximation and the n-point approximation from the original Gaussian rule.
The precision argument acts similarly to the WorkingPrecision option used in many Wolfram Language numeric functions; it is not at all like the PrecisionGoal option. If n is too small to allow for a high-precision result, extra precision in a result will not be meaningful.

Examples

Basic Examples (2) 

The abscissas, weights and error weights for a 7-point Salzer-Piessens rule:

In[1]:=
ResourceFunction["SalzerPiessensInversionWeights"][3]
Out[1]=

Use the specified precision:

In[2]:=
ResourceFunction["SalzerPiessensInversionWeights"][3, 20]
Out[2]=

Applications (7) 

A function to be transformed:

In[3]:=
fun = s |-> 1/Sqrt[1 + s^2];

Generate a 21-point Salzer-Piessens rule at high precision:

In[4]:=
spr = ResourceFunction["SalzerPiessensInversionWeights"][10, 25];

Numerically evaluate its inverse Laplace transform at a given point:

In[5]:=
t0 = 53/10; res = (spr[[All, 2]] . fun[1/spr[[All, 1]]/t0])/t0
Out[5]=

Compute the error estimate:

In[6]:=
err = (spr[[All, 3]] . fun[1/spr[[All, 1]]/t0])/t0
Out[6]=

Compare with the exact answer:

In[7]:=
exact = InverseLaplaceTransform[fun[s], s, t] /. t -> t0
Out[7]=
In[8]:=
Abs[(res - exact)/exact]
Out[8]=

Plot the exact and approximate transform together:

In[9]:=
Plot[{InverseLaplaceTransform[fun[s], s, t], (spr[[All, 2]] . fun[1/spr[[All, 1]]/t])/t} // Evaluate, {t, 0, 25}, Sequence[ PlotLegends -> {"exact transform", "Salzer-Piessens approximation"}, PlotStyle -> { Thickness[Large], Directive[ Thickness[Large], Dashing[{Small, Small}]]}, WorkingPrecision -> 15.954589770191003`]]
Out[9]=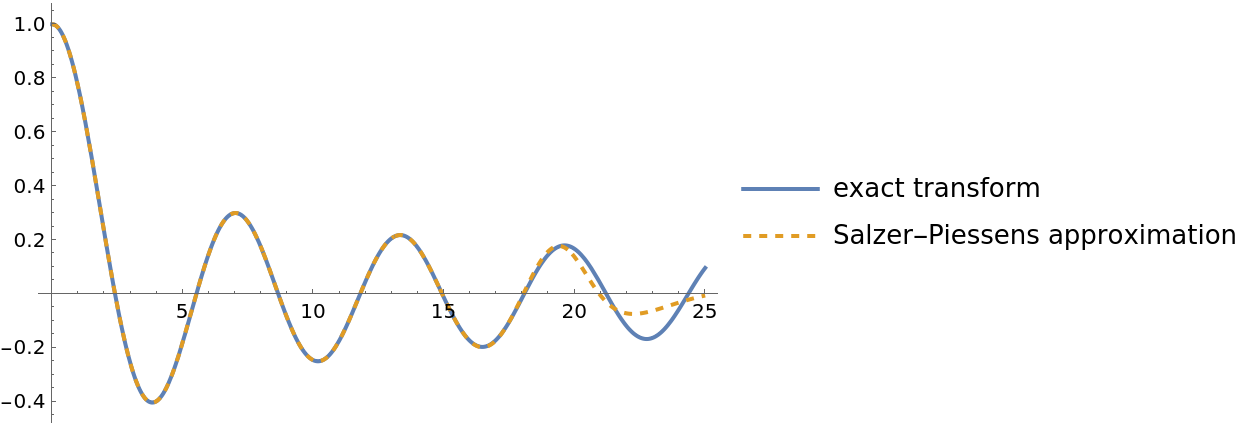

Plot the error estimate:

In[10]:=
Plot[(spr[[All, 3]] . fun[1/spr[[All, 1]]/t])/t, {t, 0, 10}, Sequence[ PlotRange -> All, WorkingPrecision -> 15.954589770191003`]]
Out[10]=

Properties and Relations (1) 

A (2 n+1)-point Salzer-Piessens rule gives the exact inverse Laplace transform for functions of the form :

In[11]:=
spr = ResourceFunction["SalzerPiessensInversionWeights"][3];
In[12]:=
(spr[[All, 2]] . Function[s, \!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(11\)]\(C[k] \*SuperscriptBox[\(s\), \(-k\)]\)\)][1/spr[[All, 1]]/t])/t // FullSimplify // Expand
Out[12]=
In[13]:=
InverseLaplaceTransform[\!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(11\)]\(C[k] \*SuperscriptBox[\(s\), \(-k\)]\)\), s, t] // Expand // N
Out[13]=

Possible Issues (3) 

A function to be transformed:

In[14]:=
fun = s |-> 1/s ArcTan[1/s];

Machine precision usually does not give sufficient accuracy due to the ill-conditioned nature of numerical Laplace transform inversion:

In[15]:=
spr1 = ResourceFunction["SalzerPiessensInversionWeights"][14];
In[16]:=
t0 = 53/10; {spr1[[All, 2]], spr1[[All, 3]]} . fun[1/spr1[[All, 1]]/t0]/t0
Out[16]=

Arbitrary precision is often necessary to get accurate results:

In[17]:=
spr2 = ResourceFunction["SalzerPiessensInversionWeights"][14, 25];
In[18]:=
t0 = 53/10; {spr2[[All, 2]], spr2[[All, 3]]} . fun[1/spr2[[All, 1]]/t0]/t0
Out[18]=

Version History

  • 1.0.0 – 23 March 2021

Source Metadata

  • Citation:
    • Piessens R., "New quadrature formulas for the numerical inversion of the Laplace transform." BIT Numerical Mathematics, vol. 9, 351–361, 1969. DOI: 10.1007/BF01935866
    • Piessens R., "Gaussian quadrature formulas for the numerical integration of Bromwich's integral and the inversion of the Laplace transform." Journal of Engineering Mathematics, vol. 5, 1–9, 1971. DOI: 10.1007/BF01535429
    • Piessens R., "Some aspects of Gaussian quadrature formulae for the numerical inversion of the Laplace transform." The Computer Journal, vol. 14, no. 4, 433–436, 1971. DOI: 10.1093/comjnl/14.4.433
    • Salzer H.E., "Orthogonal polynomials arising in the numerical evaluation of inverse Laplace transforms." Mathematical Tables and Other Aids to Computation, vol. 9, 164–177, 1955. DOI: 10.1090/S0025-5718-1955-0078498-1
    • Salzer H.E., "Additional Formulas and Tables for Orthogonal Polynomials Originating from Inversion Integrals." Journal of Mathematics and Physics, vol. 40, 72–86, 1961. DOI: 10.1002/sapm196140172

Related Resources

License Information