Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SO3TensorCommutators

Source Notebook

Compute SO(3) representation tensor commutators and anti-commutators

Contributed by: Xu-xing Geng

ResourceFunction["SO3TensorCommutators"][J,k1,q1,k2,q2,c]

gives the commutators/anti-commutators of the SO(3) irreducible tensors T[J]k1, q1 and T[J]k2, q2.

Details

Tensor objects that transform as irreducible representations of the rotation group SO(3) are important in quantum mechanics. An irreducible tensor Tk has an angular momentum quantum number k and consists of (2k+1) components Tk,q (q from −k to k) that transform into linear combinations of each other under rotational transformations.
Use c=-1 to get the commutators [T[J]k1, q1,T[J]k2, q2]-1 between T[J]k1, q1 and T[J]k2, q2, where k1 and k2 are the k1-order and k2-order tensors with angular momentum J and the corresponding q1 and q2 components respectively.
Use c=1 to get the anti-commutation relations [T[J]k1, q1,T[J]k2, q2]1 between the tensors T[J]k1, q1 and T[J]k2, q2, where k1 and k2 are the k1-order and k2-order tensors with angular momentum J and the corresponding q1 and q2 components respectively.

Examples

Basic Examples (2) 

The commutator of two irreducible tensors T[1/2]1,0 and T[1/2]1,-1 with angular momentum J=1/2 is given by:

In[1]:=
ResourceFunction["SO3TensorCommutators"][1/2, 1, 0, 1, -1, -1]
Out[1]=

The anti-commutator of the two tensors T[1/2]1,0 and T[1/2]1,-1 with angular momentum J=1/2 is given by:

In[2]:=
ResourceFunction["SO3TensorCommutators"][1/2, 1, 0, 1, -1, 1]
Out[2]=

Scope (3) 

The commutator of two irreducible tensors T[4]2,1 and T[4]3,-1 with large angular momentum J=4 is given by:

In[3]:=
ResourceFunction["SO3TensorCommutators"][4, 2, 1, 3, -1, -1]
Out[3]=

The anti-commutator of two irreducible tensors T[4]2,1 and T[4]3,-1 with large angular momentum J=4 is given by:

In[4]:=
ResourceFunction["SO3TensorCommutators"][4, 2, 1, 3, -1, 1]
Out[4]=

All commutators between two irreducible tensors and with large angular momentum J=1 are given by:

In[5]:=
Table[Subscript[ StringReplace[ToString[Comm], "Comm" -> ""][\!\(TraditionalForm\` \*SubscriptBox[\(T[1]\), \(1, i\)]\), \!\(TraditionalForm\` \*SubscriptBox[\(T[1]\), \(1, j\)]\)], -1] == ResourceFunction["SO3TensorCommutators"][1, 1, i, 1, j, -1], {i, -1, 1}, {j, -1, 1}] // TableForm
Out[5]=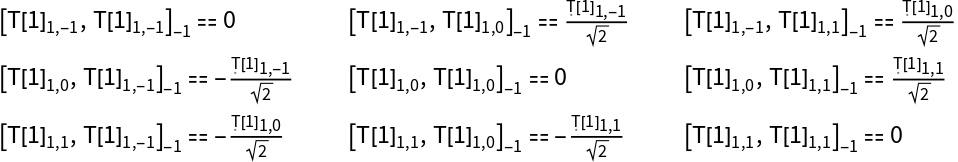

All commutators between two irreducible tensors and with large angular momentum J=1 are given by:

In[6]:=
Table[Subscript[ StringReplace[ToString[Comm], "Comm" -> ""][\!\(TraditionalForm\` \*SubscriptBox[\(T[1]\), \(1, i\)]\), \!\(TraditionalForm\` \*SubscriptBox[\(T[1]\), \(1, j\)]\)], 1] == ResourceFunction["SO3TensorCommutators"][1, 1, i, 1, j, 1], {i, -1, 1}, {j, -1, 1}] // TableForm
Out[6]=

Publisher

Xuxing geng

Requirements

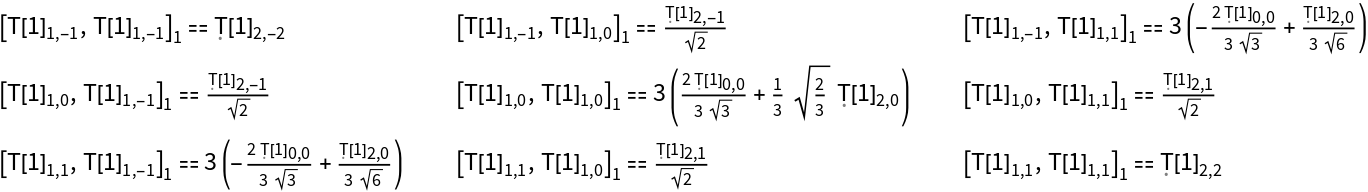Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 23 August 2024

Source Metadata

  • Citation:
    • Kupriyanov D V, Mishina O S, Sokolov I M, et al. Multimode entanglement of light and atomic ensembles via off-resonant coherent forward scattering[J]. Physical Review A, American Physical Society (APS), 2005, 71(3).

Related Resources

License Information