Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Transform a unit into a product of constants
ResourceFunction["SIConstantConvert"][unit] transforms unit into a product of the seven SI defining constants. | |
ResourceFunction["SIConstantConvert"][quantitydistribution] transforms quantitydistribution into a quantity distribution with units that are the product of the seven SI defining constants. |
Convert the height of the Empire State building to a combination of physical constants:
| In[1]:= |
| Out[1]= |
Transform the seven SI base units into products of constants:
| In[2]:= | ![SIBaseUnits = AssociationThread[{"time", "length", "mass", "electric-current", "thermodynamic-temperature", "amount-of-substance", "luminous-intensity"}, {Quantity["Seconds"], Quantity["Meters"], Quantity["Kilograms"], Quantity["Amperes"], Quantity["Kelvins"], Quantity["Moles"], Quantity["Candelas"]}]](https://www.wolframcloud.com/obj/resourcesystem/images/95f/95f636e9-dfbb-4973-abe0-2f42a1cdf3f1/519e7d771865cd02.png) |
| Out[2]= |  |
| In[3]:= |
| Out[3]= |  |
Fit a model to data with units:
| In[4]:= |
Convert the distribution to a form with the SI constants:
| In[5]:= |
| Out[5]= |
Transform the 22 SI derived units with special names to products of constants:
| In[6]:= | ![SIDerivedUnitsWithSpecialNames = AssociationThread[{"plane-angle", "solid-angle", "frequency", "force", "pressure-stress", "energy-work-amount-of-heat", "power-radiant-flux", "electric-charge", "electric-potential-difference", "capacitance", "electric-resistance", "electric-conductance", "magnetic-flux", "magnetic-flux-density", "inductance", "Celsius-temperature", "luminous-flux", "illuminance", "activity-referred-to-a-radionuclide", "absorbed-dose-kerma", "dose-equivalent", "catalytic-activity"}, {Quantity["Radians"], Quantity["Steradians"], Quantity["Hertz"], Quantity["Newtons"], Quantity["Pascals"], Quantity["Joules"], Quantity["Watts"], Quantity["Coulombs"], Quantity["Volt"], Quantity["Farads"], Quantity["Ohm"], Quantity["Siemens"], Quantity["Weber"], Quantity["Teslas"], Quantity["Henry"], Quantity["DegreesCelsius"], Quantity["Lumen"], Quantity["Lux"], Quantity["Becquerels"], Quantity["Gray"], Quantity["Sieverts"], Quantity["Katals"]}]](https://www.wolframcloud.com/obj/resourcesystem/images/95f/95f636e9-dfbb-4973-abe0-2f42a1cdf3f1/16f0d125f63aa3c6.png) |
| Out[6]= | 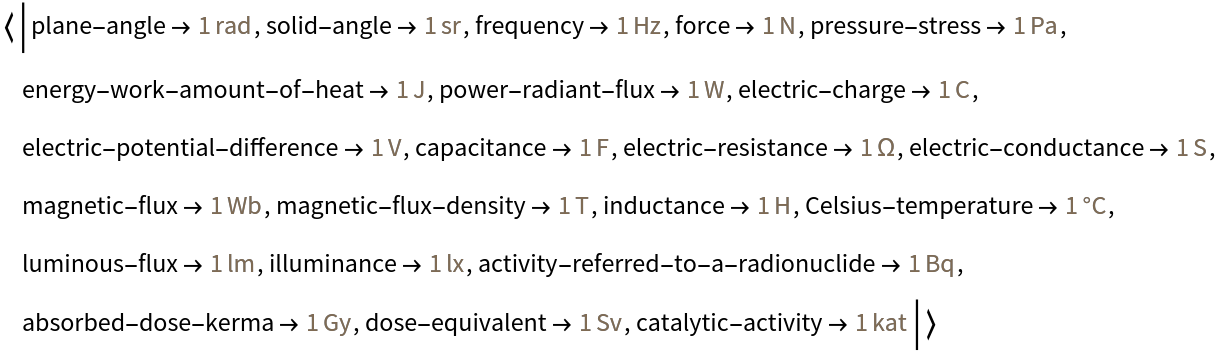 |
| In[7]:= |
| Out[7]= |  |
Transform physical quantities expressed in derived units with only the seven base units to products of constants:
| In[8]:= | ![derivedQuantitiesInSIUnits = AssociationThread[{"area", "volume", "speed-velocity", "acceleration", "wavenumber", "density-mass-density", "surface-density", "specific-volume", "current-density", "magnetic-field-strength", "amount-of-substance-concentration", "mass-concentration", "luminance"}, {Quantity["Meters"], Quantity["Meters"], Quantity["Meters"/"Seconds"], Quantity["Meters"/"Seconds"], Quantity["Meters"], Quantity["Kilograms"/"Meters"], Quantity["Kilograms" "Meters"], Quantity["Meters" "Kilograms"], Quantity["Amperes" "Meters"], Quantity["Amperes" "Meters"], Quantity["Moles" "Meters"], Quantity["Kilograms" "Meters"], Quantity["Candelas" "Meters"]}]](https://www.wolframcloud.com/obj/resourcesystem/images/95f/95f636e9-dfbb-4973-abe0-2f42a1cdf3f1/601b80096473b517.png) |
| Out[8]= | 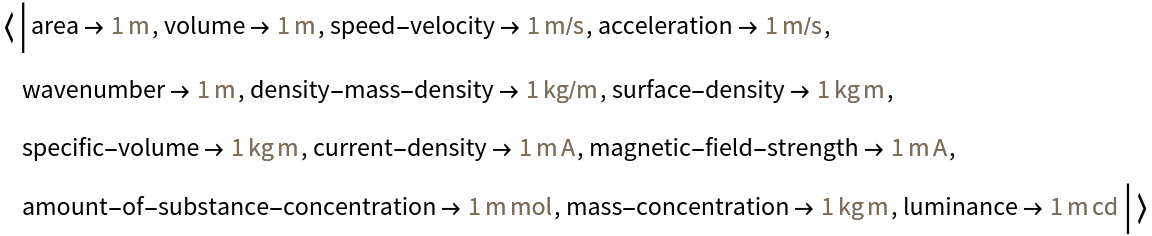 |
| In[9]:= |
| Out[9]= |  |
Transform SI coherent derived units whose names and symbols include coherent derived units with special names and symbols to products of constants:
| In[10]:= | ![SICoherentDerivedUnitsWhoseNamesAndSymbolsIncludesSICoherentDerivedUnitsWithSpecialNamesAndSymbols = AssociationThread[{"dynamic-viscosity", "moment-of-force", "surface-tension", "angular-velocity-angular-frequency", "angular-acceleration", "heat-flux-density-irradiance", "heat-capacity-entropy", "specific-heat-capacity-specific-entropy",
"specific-energy", "thermal-conductivity", "energy-density", "electric-field-strength", "electric-charge-density", "surface-charge-density", "electric-flux-density", "permittivity", "permeability", "molar-energy", "molar-entropy-molar-heat-capacity", "exposure-x-ray-\[Gamma]-ray",
"absorbed-dose-rate", "radiant-intensity", "radiance", "catalytic-activity-concentration"}, {Quantity[None, "Pascals" "Seconds"], Quantity[None, "Meters" "Newtons"], Quantity[None, ("Newtons")/("Meters")], Quantity["Radians" ("Seconds")^-1], Quantity["Radians" ("Seconds")^-2], Quantity["Watts" ("Meters")^-2], Quantity["Joules"/"Kelvins"], Quantity["Joules" ("Kelvins")^-1 ("Kilograms")^-1], Quantity["Joules" ("Kilograms")^-1], Quantity["Watts" ("Meters")^-1 ("Kelvins")^-1], Quantity["Joules" ("Meters")^-3], Quantity["Volts" ("Meters")^-1], Quantity["Coulombs" ("Meters")^-3], Quantity["Coulombs" ("Meters")^-2], Quantity["Coulombs" ("Meters")^-2], Quantity["Farads" ("Meters")^-1], Quantity["Henries" ("Meters")^-1], Quantity["Joules" ("Moles")^-1],
Quantity["Joules" ("Kelvins")^-1 ("Moles")^-1], Quantity["Coulombs" ("Kilograms")^-1], Quantity["Grays" ("Seconds")^-1], Quantity["Watts" ("Steradians")^-1], Quantity["Watts" ("Steradians")^-1 ("Meters")^-2], Quantity["Katals" ("Meters")^-3]}]](https://www.wolframcloud.com/obj/resourcesystem/images/95f/95f636e9-dfbb-4973-abe0-2f42a1cdf3f1/1858d0efb4e6442d.png) |
| Out[10]= | 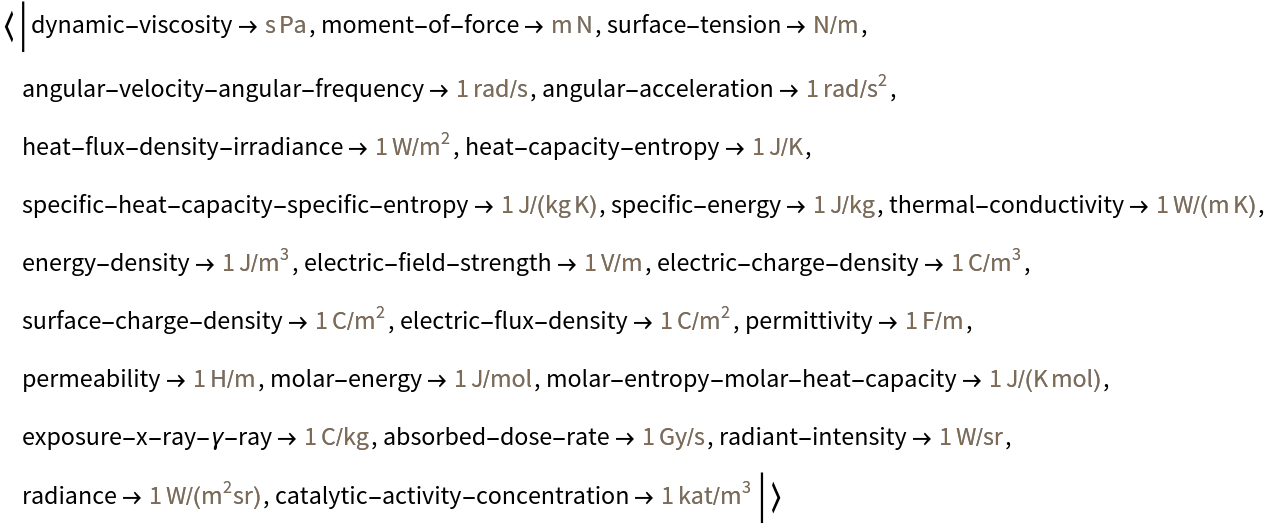 |
| In[11]:= | ![{#, ResourceFunction["SIConstantConvert"][#], N[ResourceFunction[
"SIConstantConvert"][#]]} & /@ SICoherentDerivedUnitsWhoseNamesAndSymbolsIncludesSICoherentDerivedUnitsWithSpecialNamesAndSymbols](https://www.wolframcloud.com/obj/resourcesystem/images/95f/95f636e9-dfbb-4973-abe0-2f42a1cdf3f1/24026f6a17fa2c35.png) |
| Out[11]= |  |
Estimate the distribution of the daily mean temperature in Chicago in the summer of 2015:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= | 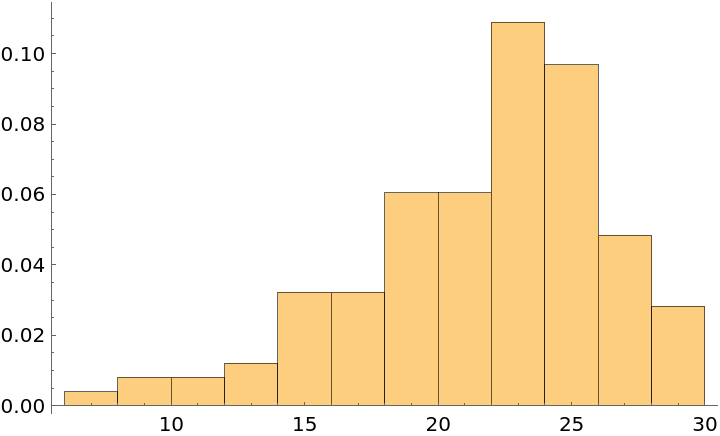 |
Fit the distribution to PERTDistribution:
| In[14]:= |
| Out[14]= |
Check goodness of fit:
| In[15]:= |
| Out[15]= | 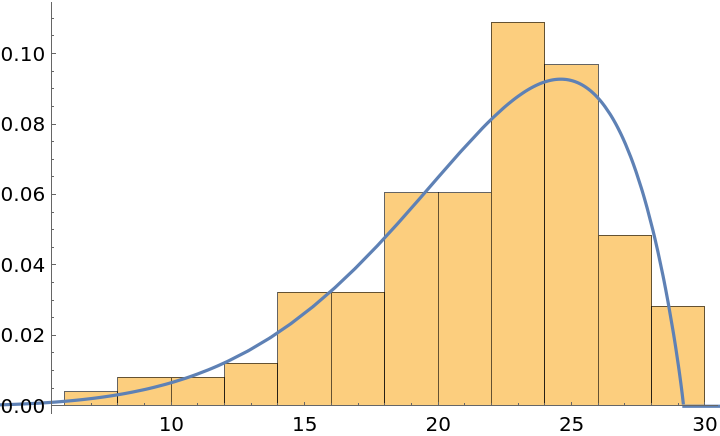 |
Find the estimated distribution for temperature with the SI constants:
| In[16]:= |
| Out[16]= |
Find the mean and standard deviation:
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
Compare the variance and trimmed variance:
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
Find the first five moments:
| In[21]:= |
| Out[21]= | 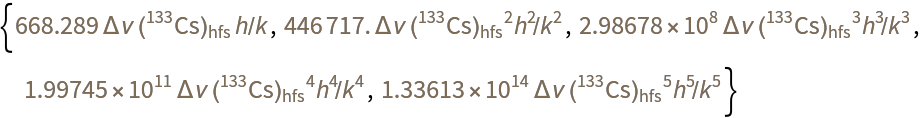 |
Convert all instances of physical quantities in the SI Brochure to products of constants:
| In[22]:= | ![SIBrochurePhysicalUnits = <|"time" -> Quantity[1, "Seconds"], "length" -> Quantity[1, "Meters"], "mass" -> Quantity[1, "Kilograms"], "electric-current" -> Quantity[1, "Amperes"], "thermodynamic-temperature" -> Quantity[1, "Kelvins"], "amount-of-substance" -> Quantity[1, "Moles"], "luminous-intensity" -> Quantity[1, "Candelas"], "area" -> Quantity[1, "Meters"], "volume" -> Quantity[1, "Meters"],
"speed-velocity" -> Quantity[1, ("Meters")/("Seconds")], "acceleration" -> Quantity[1, ("Meters")/("Seconds")], "wavenumber" -> Quantity[1, "Meters"], "density-mass-density" -> Quantity[1, ("Kilograms")/("Meters")], "surface-density" -> Quantity[1, "Kilograms" "Meters"], "specific-volume" -> Quantity[1, "Kilograms" "Meters"], "current-density" -> Quantity[1, "Amperes" "Meters"], "magnetic-field-strength" -> Quantity[1, "Amperes" "Meters"], "amount-of-substance-concentration" -> Quantity[1, "Meters" "Moles"], "mass-concentration" -> Quantity[1, "Kilograms" "Meters"], "luminance" -> Quantity[1, "Candelas" "Meters"], "dynamic-viscosity" -> Quantity[1, "Pascals" "Seconds"], "moment-of-force" -> Quantity[1, "Meters" "Newtons"], "surface-tension" -> Quantity[1, (("Newtons")/("Meters"))], "angular-velocity-angular-frequency" -> Quantity[1, ("Radians")/("Seconds")], "angular-acceleration" -> Quantity[1, ("Radians")/("Seconds")^2], "heat-flux-density-irradiance" -> Quantity[1, ("Watts")/("Meters")^2], "heat-capacity-entropy" -> Quantity[1, ("Joules")/("Kelvins")], "specific-heat-capacity-specific-entropy" -> Quantity[1, ("Joules")/("Kelvins" "Kilograms")], "specific-energy" -> Quantity[1, ("Joules")/("Kilograms")], "thermal-conductivity" -> Quantity[1, ("Watts")/("Kelvins" "Meters")], "energy-density" -> Quantity[1, ("Joules")/("Meters")^3], "electric-field-strength" -> Quantity[1, ("Volts")/("Meters")], "electric-charge-density" -> Quantity[1, ("Coulombs")/("Meters")^3], "surface-charge-density" -> Quantity[1, ("Coulombs")/("Meters")^2],
"electric-flux-density" -> Quantity[1, ("Coulombs")/("Meters")^2],
"permittivity" -> Quantity[1, ("Farads")/("Meters")], "permeability" -> Quantity[1, ("Henries")/("Meters")], "molar-energy" -> Quantity[1, ("Joules")/("Moles")], "molar-entropy-molar-heat-capacity" -> Quantity[1, ("Joules")/("Kelvins" "Moles")], "exposure-x-ray-\[Gamma]-ray" -> Quantity[1, ("Coulombs")/("Kilograms")], "absorbed-dose-rate" -> Quantity[1, ("Grays")/("Seconds")], "radiant-intensity" -> Quantity[1, ("Watts")/("Steradians")], "radiance" -> Quantity[1, ("Watts")/(("Meters")^2 "Steradians")], "catalytic-activity-concentration" -> Quantity[1, ("Katals")/("Meters")^3]|>;](https://www.wolframcloud.com/obj/resourcesystem/images/95f/95f636e9-dfbb-4973-abe0-2f42a1cdf3f1/1995c5b5ae0b2bc1.png) |
| In[23]:= |
| Out[23]= |  |
Transform units with angles:
| In[24]:= |
| Out[24]= | 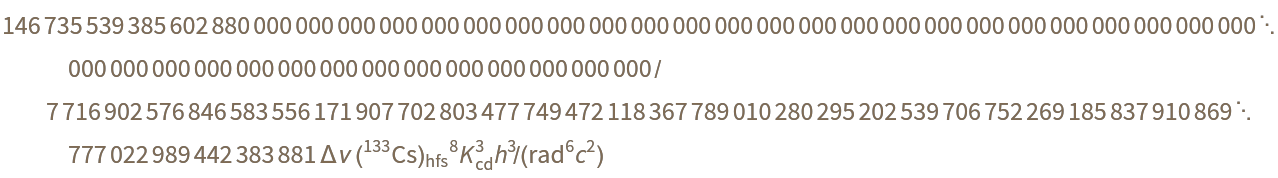 |
This work is licensed under a Creative Commons Attribution 4.0 International License