Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RungeKuttaDSolve

Source Notebook

Solve differential equations using one of the Runge–Kutta or related methods

Contributed by: Jason Martinez

ResourceFunction["RungeKuttaDSolve"][eqns,u,{x,xmin,xmax}, method]

finds a numerical solution to the ordinary differential equations eqns for the function u with the independent variable x in the range xmin to xmax using the specified method.

ResourceFunction["RungeKuttaDSolve"][eqns,u,{x,xmin,xmax},property,method]

returns a specific property for the numerical calculation.

Details and Options

ResourceFunction["RungeKuttaDSolve"] gives results in terms of InterpolatingFunction objects.
ResourceFunction["RungeKuttaDSolve"] supports most of the functionality and options for NDSolve but inserts the proper method options for the specified method.
method specifications include:
"DOPRI"Dormand–Prince method
"ExplicitEuler"Forward Euler method
"ExplicitMidpoint"Explicit midpoint method
"Heun"Heun's method
"ImplicitEuler"backward Euler method
"ImplicitMidpoint"implicit midpoint method
"RK3"3rd order Runge–Kutta method
"RK4"4th order Runge–Kutta method
"RKBS"Bogacki–Shampine method
"RKF"Runge–Kutta–Fehlberg method
The function u must depend only on the single variable x.
The differential equations must contain enough initial or boundary conditions to determine the solutions for u completely.
property can take any of the following values:
"Solution"interpolation function for the solution to u
"Steps"Stepwise results
"ButcherTableau"Butcher tableau for the method
"PropertyAssociation" can be used to return an Association of the properties.

Examples

Basic Examples (1) 

Solve a differential equation using the fourth order Runge-Kutta method:

In[1]:=
ResourceFunction[ "RungeKuttaDSolve"][{y'[x] == y[x] Cos[x + y[x]], y[0] == 1}, y, {x, 0, 30}, "RK4"]
Out[1]=

Scope (3) 

Find the Butcher tableau for the Dormand–Prince method:

In[2]:=
ResourceFunction[ "RungeKuttaDSolve"][{y'[x] == y[x] Cos[x + y[x]], y[0] == 1}, y, {x, 0, 30}, "ButcherTableau", "DOPRI"]
Out[2]=

Compute the steps to determine the interpolation function:

In[3]:=
ResourceFunction[ "RungeKuttaDSolve"][{y'[x] == -2 x y[x], y[0] == 2}, y, {x, 1, 3}, "Steps", "RK4"]
Out[3]=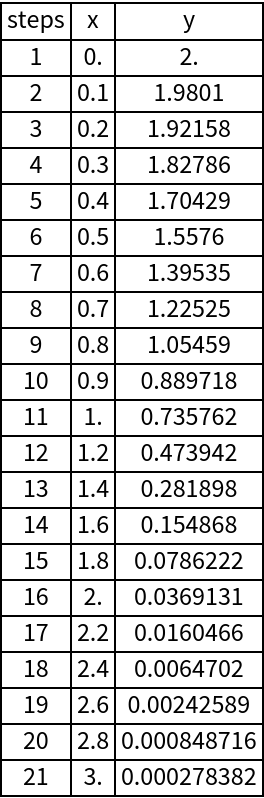

Get a property association of all properties:

In[4]:=
ResourceFunction[ "RungeKuttaDSolve"][{x''[t] + 1/10 x'[t] + Sin[x[t]] == 1/2 Cos[t], x[0] == x'[0] == 0}, x, {t, 0, 100}, "PropertyAssociation", "ExplicitEuler"]
Out[4]=

Version History

  • 1.0.0 – 08 August 2022

Related Resources

License Information