Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Conduct a randomness test on a sequence of random reals between 0 and 1 using run lengths of increasing subsequences
ResourceFunction["RunLengthRandomnessTest"][sequence] uses lengths of increasing runs to test the randomness of sequence and returns an associated p-value. | |
ResourceFunction["RunLengthRandomnessTest"][sequence,"property"] uses lengths of increasing runs and returns the associated property. |
| "TestStatistic" | returns the test statistic |
| "PValue" | returns the p-value associated with the test |
Generate a sequence of random integers:
| In[1]:= |
Visualize the sequence:
| In[2]:= |
| Out[2]= |  |
Apply a run length-based test:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Generate a sequence of random integers:
| In[5]:= |
| In[6]:= |
Visualize the sequence:
| In[7]:= |
| Out[7]= |  |
Attempt to reject a non-random sequence:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Visualize the sampling distribution of the test statistic:
| In[10]:= |
| In[11]:= |
| Out[11]= | 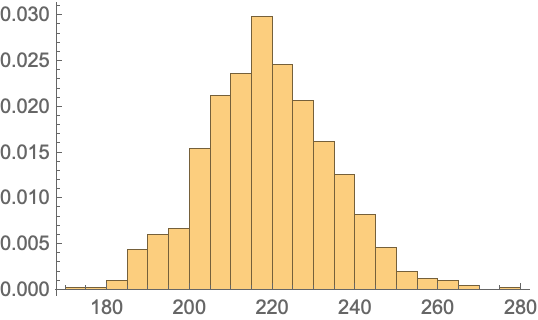 |
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= | 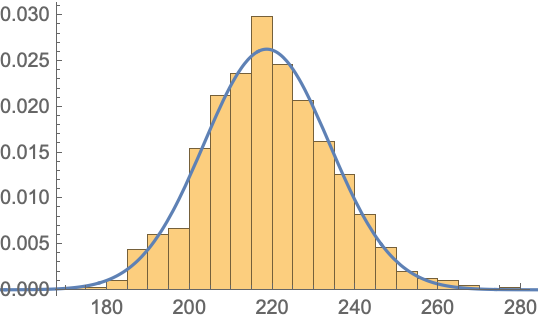 |
This work is licensed under a Creative Commons Attribution 4.0 International License