Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Conduct a runs up–based randomness test on a sequence of random reals between 0 and 1
ResourceFunction["RunCountRandomnessTest"][sequence] counts the number of increasing runs to assess randomness of sequence and returns an associated p-value. | |
ResourceFunction["RunCountRandomnessTest"][sequence,"property"] counts the number of increasing runs to assess randomness and returns the specified property. |
| "TestStatistic" | returns the test statistic |
| "PValue" | returns the p-value associated with the test |
Generate a sequence of random integers:
| In[1]:= |
Visualize the sequence:
| In[2]:= |
| Out[2]= |  |
Apply a run count-based test to the sequence:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Generate a sequence of random integers:
| In[5]:= |
| In[6]:= |
Visualize the sequence:
| In[7]:= |
| Out[7]= |  |
Attempt to reject a non-random sequence:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
This test is not very powerful and fails to reject non-random sequences that repeat over longer intervals on occasion. Ideally, it should be used in conjunction with another test:
| In[10]:= |
| In[11]:= |
| In[12]:= |
| Out[12]= |  |
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Visualize the sampling distribution of the test statistic:
| In[15]:= |
| In[16]:= |
| Out[16]= | 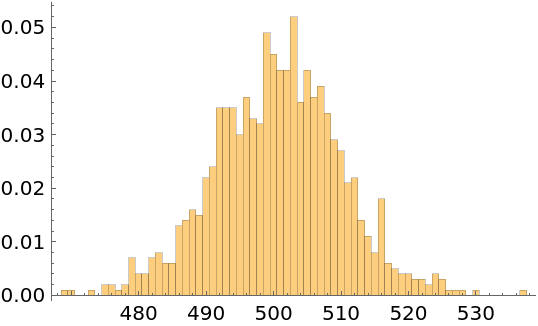 |
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= | 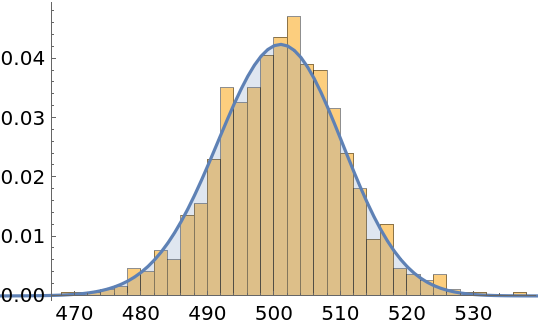 |
This work is licensed under a Creative Commons Attribution 4.0 International License