Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RuledSurfacePlot

Source Notebook

Plot a ruled surface

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["RuledSurfacePlot"][c1,c2,u]

plots a ruled surface from the curves c1 and c2 that are parameterized by the variable u.

ResourceFunction["RuledSurfacePlot"][c1,c2,{u,umin,umax},{v,vmin,vmax}]

plots a ruled surface with u varying from umin to umax and v varying from vmin to vmax.

Details and Options

A ruled surface is generated by the continuous motion of a straight line passing through two curves c1 and c2, and has a parametrization of the form , where c1 is the directrix curve and c2 is called the director curve or the ruling.
ResourceFunction["RuledSurfacePlot"] has the same options as ParametricPlot3D.
ResourceFunction["RuledSurfacePlot"][c1,c2,u] is equivalent to ResourceFunction["RuledSurfacePlot"][c1,c2,{u,-π,π},{v,-π,π}].

Examples

Basic Examples (2) 

A simple ruled surface:

In[1]:=
Show[ResourceFunction[ "RuledSurfacePlot"][{Cos[u], Sin[u], 0}, {Sin[u], Cos[u], 1}, u], ParametricPlot3D[{{Cos[u], Sin[u], 0}, {Cos[u], Sin[u], g}}, {u, 0, 2 \[Pi]}]]
Out[1]=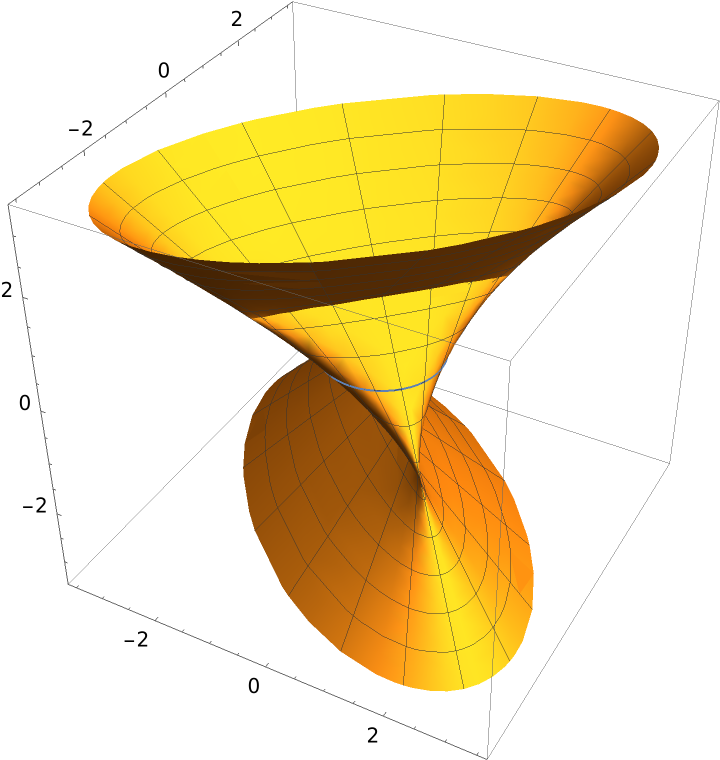

This Manipulate shows how the surface is generated, the right line moves around intersecting the two curves, for definite values of u and v:

In[2]:=
Manipulate[ Show[ResourceFunction[ "RuledSurfacePlot"][{Cos[u], Sin[u], 0}, {Sin[u], Cos[u], 1}, {u, -$MachineEpsilon, uf}, {v, -3, 2}, MeshStyle -> Directive[AbsoluteThickness[0.5], Opacity[0.2]], PlotStyle -> Opacity[0.1], PlotRange -> 4], ParametricPlot3D[{{Cos[u], Sin[u], 0}, {Cos[u], Sin[u], 0} + vf {Sin[u], Cos[u], 1}}, {u, 0, 2 \[Pi]}, PlotStyle -> AbsoluteThickness[4]], Graphics3D[{Directive[AbsoluteThickness[3], ColorData[97, 3]], Line[{{Cos[uf], Sin[uf], 0}, {Cos[uf], Sin[uf], 0} + vf {Sin[uf], Cos[uf], 1}}]}]], {{uf, 2 \[Pi]}, 0, 2 \[Pi]}, {vf, -3, 2}, SaveDefinitions -> True, ControlPlacement -> Top]
Out[2]=

Scope (2) 

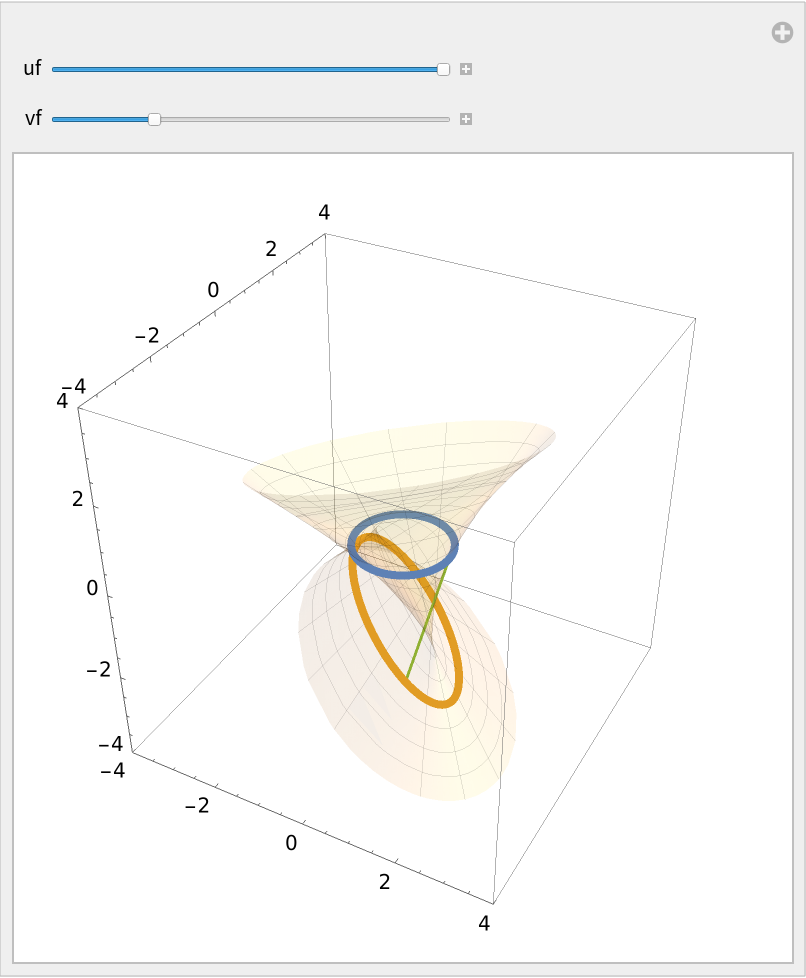Modify the default ranges:

In[3]:=
ResourceFunction[ "RuledSurfacePlot"][{Cos[u], Sin[u], 0}, {Sin[u], Cos[u], 1}, {u, 0, \[Pi]}, {v, -\[Pi], \[Pi]}, MeshFunctions -> {#4 &}]
Out[3]=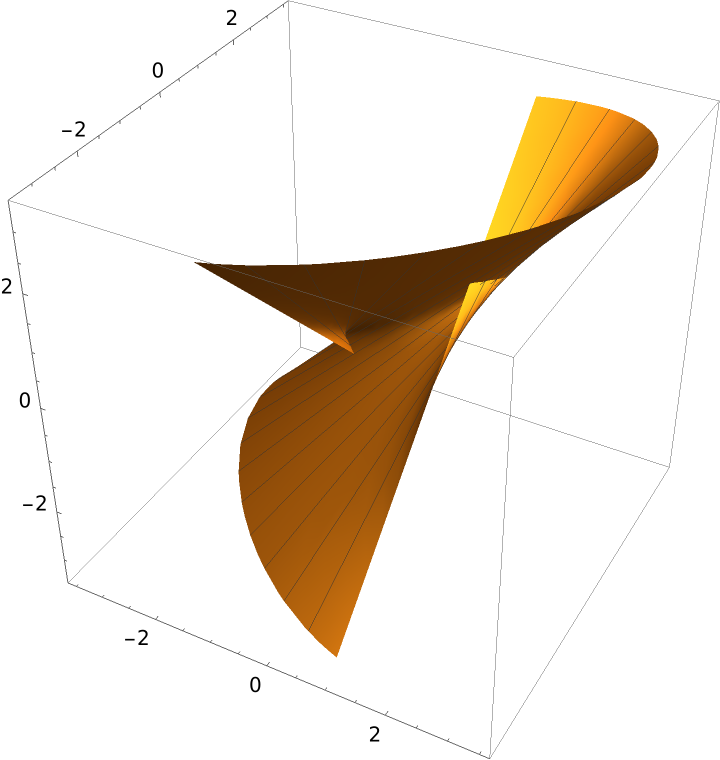

Modify the options for enhanced viewing:

In[4]:=
ResourceFunction[ "RuledSurfacePlot"][{Cos[u], Sin[u], 0}, {Sin[u], Cos[u], 1}, u, PlotStyle -> Directive[Opacity[0.5], Yellow], MeshFunctions -> {#4 &}, MeshShading -> {Red, Automatic}]
Out[4]=

Applications (3) 

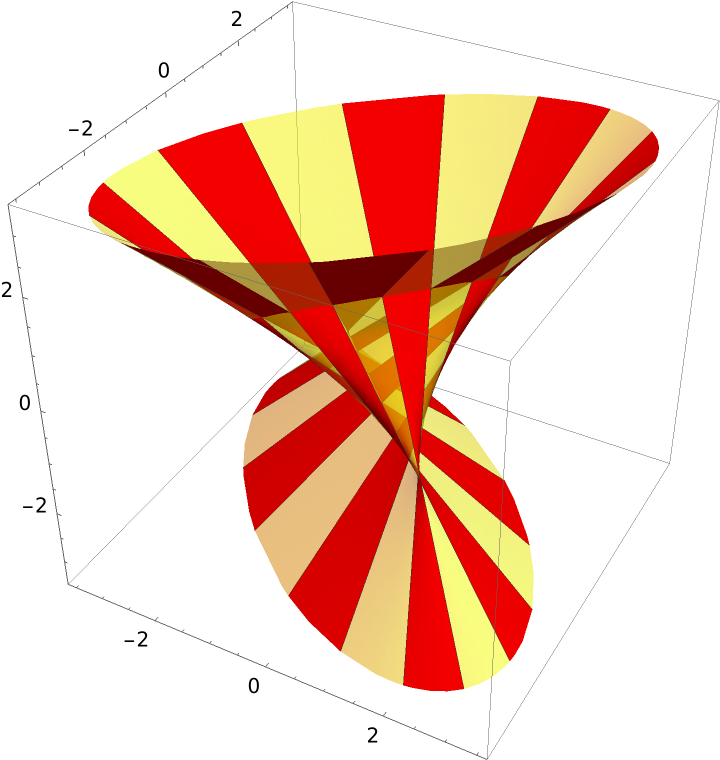Plot the generalized hyperbolic paraboloid:

In[5]:=
With[{a = 1, b = -1}, ResourceFunction[ "RuledSurfacePlot"][{a u, 0, u^2}, {0, #, 2 u}, {u, -1, 1}, {v, -1, 1}, Mesh -> {30, 0}, BoxRatios -> {1, 1, 1}, PlotRange -> All]] & /@ {-1, 1}
Out[5]=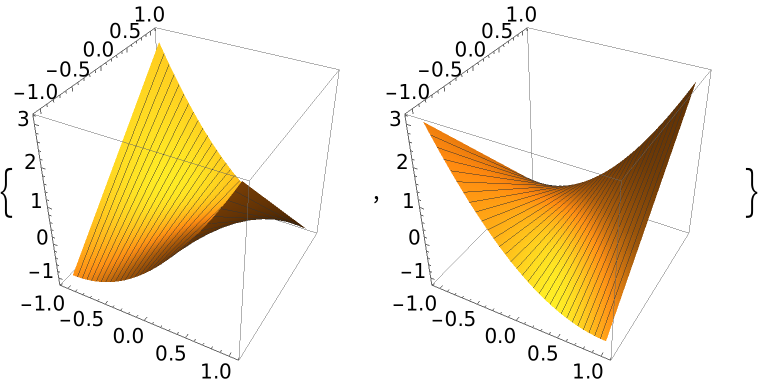

Define the Plücker conoid:

In[6]:=
Entity["Surface", "PlueckerConoid"]["ParametricEquations"][c, n][v, u]
Out[6]=

Plot the conoid:

In[7]:=
ResourceFunction[ "RuledSurfacePlot"][{0, 0, Sin[# u]}, {Cos[u], Sin[u], 0}, {u, -\[Pi], \[Pi]}, {v, -2 \[Pi], 2 \[Pi]}, Mesh -> {35, 0}, BoxRatios -> {1, 1, 1/2}, PlotPoints -> {10, 120}] & /@ Range[4]
Out[7]=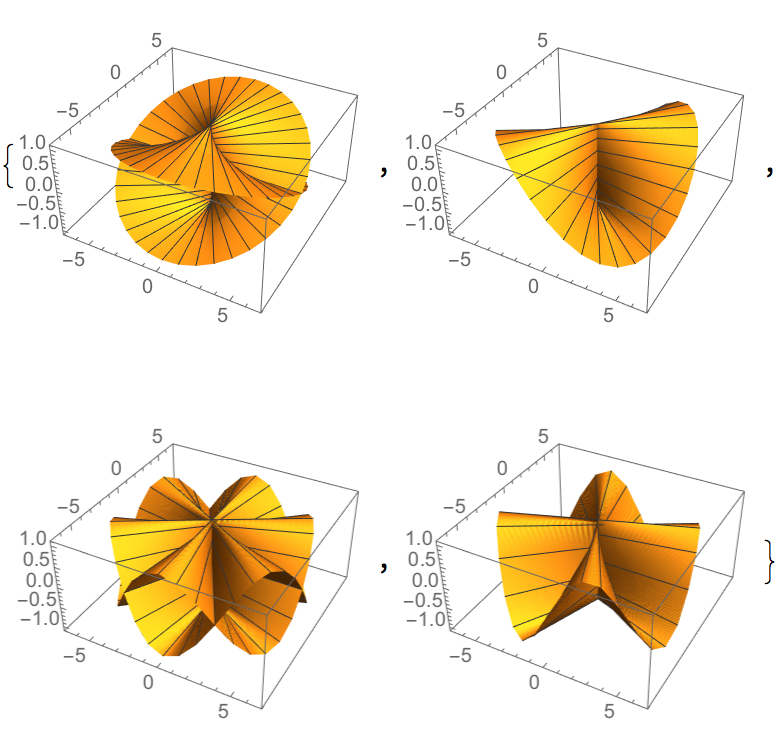

The Möbius strip as a ruled surface:

In[8]:=
ResourceFunction["RuledSurfacePlot"][ 2 {Cos[u], Sin[u], 0}, {Cos[u/2] Cos[u], Cos[u/2] Sin[u], Sin[u/2]}, {u, 0, 2 \[Pi]}, {v, -.6, .6}, PlotStyle -> Opacity[.5], Mesh -> {30, 0}]
Out[8]=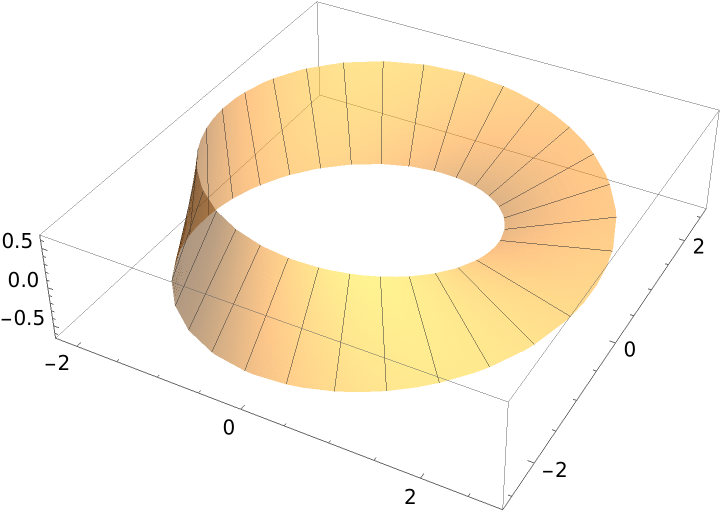

A representation of the director curve c2(u):

In[9]:=
Show[ParametricPlot3D[{Cos[u/2] Cos[u], Cos[u/2] Sin[u], Sin[u/2]}, {u, 0, 4 \[Pi]}, ViewPoint -> {2, 2, 2}, PlotRange -> All], ParametricPlot3D[ {Cos[v] Cos[u], Cos[v] Sin[u], Sin[v]}, {u, 3 \[Pi]/8, 13 \[Pi]/8}, {v, -\[Pi]/2, \[Pi]/2}, PlotStyle -> Opacity[.5]]]
Out[9]=

Properties and Relations (4) 

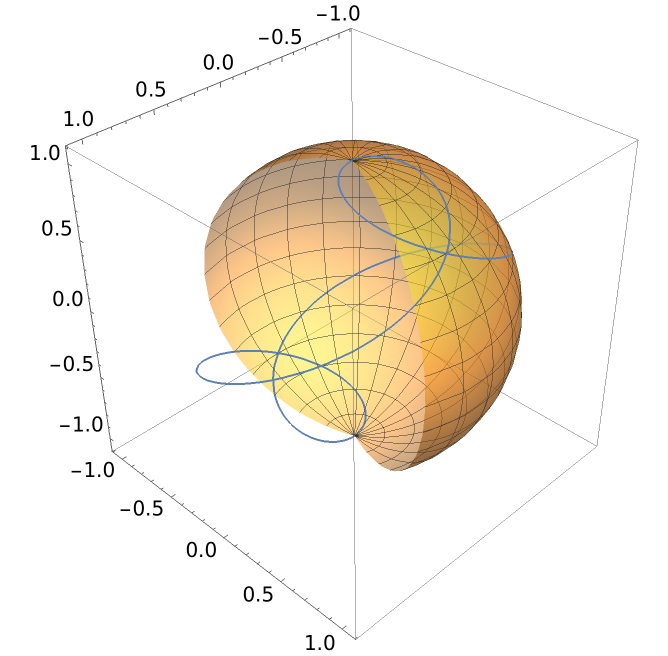An elliptical hyperboloid is doubly ruled because it can be parametrized in two ways:

In[10]:=
ellipticalhyperboloidplus[a_, b_, c_][u_, v_] := {a Cos[u] - a v Sin[u], b v Cos[u] + b Sin[u], c v} ellipticalhyperboloidminus[a_, b_, c_][u_, v_] := {a Cos[u] + a v Sin[u], -b v Cos[u] + b Sin[u], c v}

The "minus" chart could easily have been defined in terms of the "plus" one:

In[11]:=
ellipticalhyperboloidplus[a, b, c][u, v] == ellipticalhyperboloidminus[a, b, -c][u, -v] // Simplify
Out[11]=

Plot both cases:

In[12]:=
With[{a = 1, b = 2, c = 3}, GraphicsRow[{ResourceFunction[ "RuledSurfacePlot"][{a Cos[u], b Sin[u], 0}, {-a Sin[u], b Cos[u], c}, {u, 0, 3 \[Pi]/2}, {v, -1.5, 1.5}, PlotStyle -> Opacity[.5], Mesh -> {30, 0}], ResourceFunction[ "RuledSurfacePlot"][{a Cos[u], b Sin[u], 0}, {a Sin[u], -b Cos[u], c}, {u, 0, 3 \[Pi]/2}, {v, -1.5, 1.5}, PlotStyle -> Opacity[.5], Mesh -> {20, 0}]}]]
Out[12]=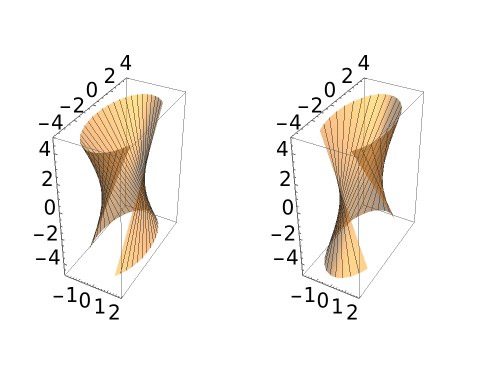

The Gaussian curvature of a ruled surface is everywhere nonpositive:

In[13]:=
gc = ResourceFunction["GaussianCurvature"][ 2 { Cos[u], Sin[u], 0} + v {Cos[u/2] Cos[u], Cos[u/2] Sin[u], Sin[u/2]}, {u, v}]
Out[13]=
In[14]:=
FullSimplify[gc <= 0, {u, v} \[Element] Reals]
Out[14]=

This plot exhibits its minima, corresponding to regions which are especially distorted:

In[15]:=
Plot3D[Evaluate[gc], {u, \[Pi], 5 \[Pi]}, {v, -.6, .6}, PlotRange -> All]
Out[15]=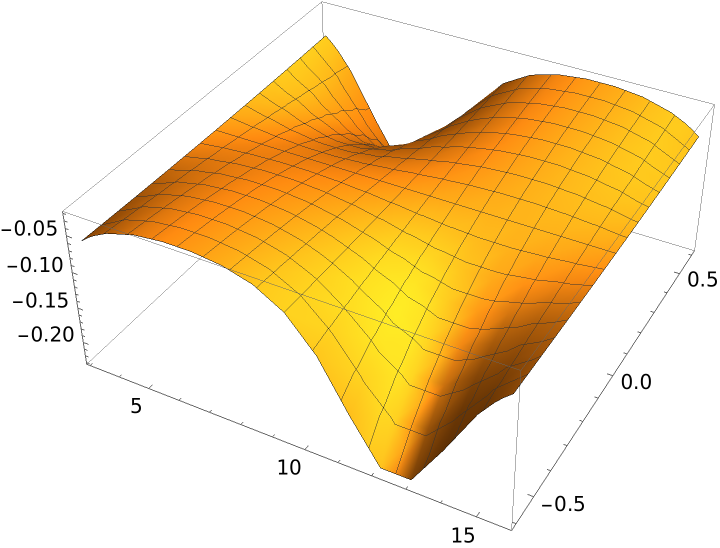

Generalized cylinders and cones have the form of a ruled surface:

In[16]:=
cylinder[p_, \[Gamma]_][v_] := \[Gamma] + v p cone[p_, \[Gamma]_][v_] := (1 - v) p + v \[Gamma]

A figure-eight curve:

In[17]:=
eight[t_] := {Sin[t], Sin[t] Cos[t], 0}

Parametrizations of a generalized cylinder and cone using a figure-eight curve:

In[18]:=
cylinder[{0, 1, 1}, eight[u]][v]
Out[18]=
In[19]:=
cone[{0, 0, 0}, 1/2 {1, 1, 4} + 2 eight[u]][v]
Out[19]=

Plot the surfaces:

In[20]:=
GraphicsRow[{ResourceFunction[ "RuledSurfacePlot"][{Sin[u], Cos[u] Sin[u], 0}, {0, 1, 1}, {u, 0, 2 \[Pi]}, {v, 0, 2}, PlotPoints -> {40, 15}, Mesh -> {30, {0}}], ResourceFunction[ "RuledSurfacePlot"][{0, 0, 0}, {1/2 + 2 Sin[u], 1/2 + 2 Cos[u] Sin[u], 2 }, {u, 0, 2 \[Pi]}, {v, -3, 3}, PlotPoints -> {40, 15}, Mesh -> {30, 0}]}]
Out[20]=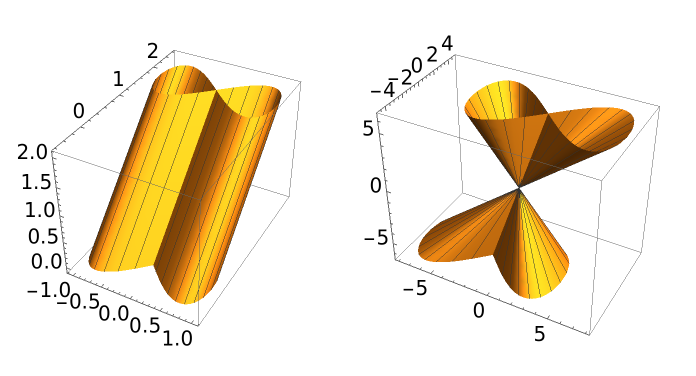

If the Gaussian curvature of a ruled surface is everywhere zero, then it is said to be a flat surface:

In[21]:=
ResourceFunction["GaussianCurvature"][ cylinder[{0, 1, 1}, eight[u]][v], {u, v}]
Out[21]=
In[22]:=
ResourceFunction["GaussianCurvature"][ cone[{0, 0, 0}, 1/2 {1, 1, 4} + 2 eight[u]][v], {u, v}]
Out[22]=

The tangent developable of a space curve α is a ruled surface, whose director curve is the unit tangent vector field to α:

In[23]:=
helix = Entity["SpaceCurve", "Helix"]["ParametricEquations"][1, 3/5][ u]
Out[23]=
In[24]:=
tdhelix = ResourceFunction["TangentDevelopableSurface"][helix /. u -> t, t, {u, v}] // Simplify
Out[24]=
In[25]:=
ParametricPlot3D[Evaluate[tdhelix], {u, 0, 4 \[Pi]}, {v, -3, 3}, Mesh -> {30, {0}}]
Out[25]=
In[26]:=
ResourceFunction["RuledSurfacePlot"][helix, Echo@ResourceFunction["TangentVector"][helix, u], {u, 0, 4 \[Pi]}, {t, -3, 3}, PlotPoints -> {40, 15}, Mesh -> {30, {0}}]
Out[26]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 26 July 2021

Source Metadata

  • Citation:

Related Resources

License Information