Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a polygon with rounded corners
ResourceFunction["RoundedPolygon"][{p1,…,pn},r] represents a filled rounded polygon with points pi and rounding radius r. | |
ResourceFunction["RoundedPolygon"][{p1,…,pn},{r1,…,rn}] represents a filled rounded polygon with points pi and corresponding rounding radii ri. |
A triangle with rounded corners:
| In[1]:= |
|
| Out[1]= |

|
A rounded rectangle with different rounding radii for each corner:
| In[2]:= |
|
| Out[2]= |

|
Coordinates for a star-shaped polygon:
| In[3]:= |
|
Show the original polygon and the rounded version:
| In[4]:= |
|
| Out[4]= |

|
Use different rounding radii for each vertex:
| In[5]:= |
![Graphics[{{Blue, Polygon[star]}, {Yellow, ResourceFunction["RoundedPolygon"][Polygon[star], PadRight[{}, 10, {1/20, 1/8}]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/637505187c353ef8.png)
|
| Out[5]= |

|
A rounded 3D polygon:
| In[6]:= |
![Graphics3D[{FaceForm[Blue, Red], ResourceFunction["RoundedPolygon"][
Polygon[PadRight[star, {Automatic, 3}]], PadRight[{}, 10, {1/20, 1/8}]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/005cb53278b9b21a.png)
|
| Out[6]= |

|
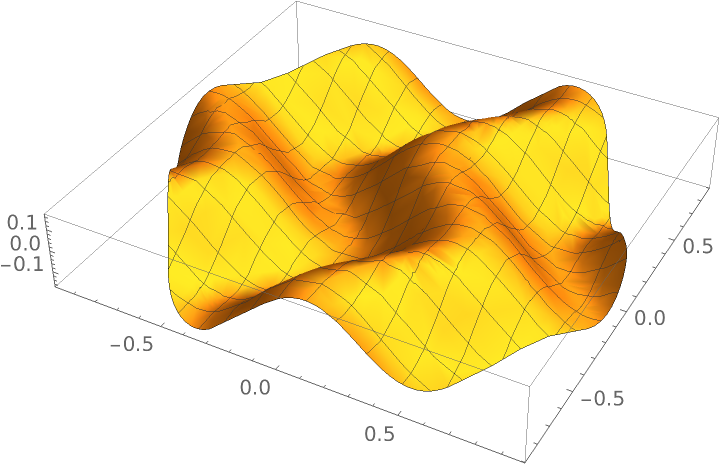
Plot a function over a rounded polygon domain:
| In[7]:= |
![Plot3D[Sin[6 x + Sin[6 y]]/6, {x, y} \[Element] ResourceFunction["RoundedPolygon"][N[CirclePoints[6]], 1/3], BoxRatios -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/610d1028d9071fe3.png)
|
| Out[7]= |
|
A polyhedron with rounded faces:
| In[8]:= |
|
| In[9]:= |
|
| Out[9]= |

|
RoundedPolygon returns a Polygon object:
| In[10]:= |
|
| Out[10]= |
|
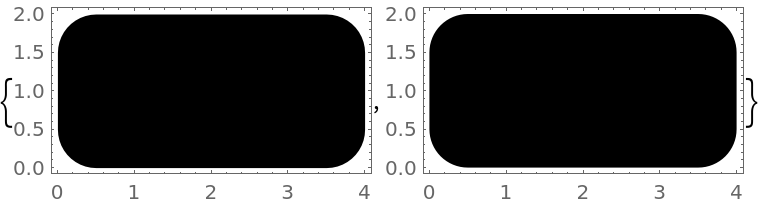
Applying RoundedPolygon to a Rectangle is equivalent to setting its RoundingRadius:
| In[11]:= |
![{Graphics[
ResourceFunction["RoundedPolygon"][Rectangle[{0., 0.}, {4., 2.}], 1/2], Frame -> True], Graphics[Rectangle[{0., 0.}, {4., 2.}, RoundingRadius -> 1/2], Frame -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/5b3d70efeac8573d.png)
|
| Out[11]= |
|
If the rounding radius is too large, RoundedPolygon may give unexpected results:
| In[12]:= |
|
| Out[12]= |

|
Use a smaller rounding radius:
| In[13]:= |
|
| Out[13]= |

|
Rounded Voronoi cells:
| In[14]:= |
![pts = RandomReal[{-2, 2}, {50, 2}];
Graphics[{Directive[ColorData[61, RandomInteger[{1, 9}]], EdgeForm[Gray]], ResourceFunction["RoundedPolygon"][#, 1/9]} & /@
MeshPrimitives[VoronoiMesh[pts], 2]]](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/324fc2613a731bd7.png)
|
| Out[14]= |

|
Use RoundedPolygon with the resource function PerforatePolygons on a truncated icosahedron:
| In[15]:= |
|
| In[16]:= |
![Graphics3D[{Gray, FaceForm[LightBlue], ResourceFunction["PerforatePolygons"][
ResourceFunction["RoundedPolygon"][#, 2/5] & /@ tric]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/7d6973c35089bc7b.png)
|
| Out[16]= |

|
Use RoundedPolygon with the resource function OutlinePolygons on a truncated icosahedron:
| In[17]:= |
![Graphics3D[{FaceForm[LightBlue], EdgeForm[], ResourceFunction["OutlinePolygons"][
ResourceFunction["RoundedPolygon"][#, 2/5] & /@ tric]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/e38/e38d4c24-36df-4ed6-b5ef-dcda16cf417b/19be6455dda406bb.png)
|
| Out[17]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License