Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RosenbrockFunction

Source Notebook

A non-convex mathematical function that is commonly used as a benchmark problem in optimization

Contributed by: Arnoud Buzing

ResourceFunction["RosenbrockFunction"][x,y]

computes the Rosenbrock function for the given x and y.

ResourceFunction["RosenbrockFunction"][x,y,a,b]

computes the Rosenbrock function for the given x and y and parameters a and b.

Details

The Rosenbrock function is defined as (a-x)2+b(y-x2)2 with typical default values a=1 and b=100.
This is sometiems refered to as the Rosenbrock banana function.

Examples

Basic Examples (2) 

Find the minimum value of the Rosenbrock function:

In[1]:=
FindMinimum[ ResourceFunction["RosenbrockFunction"][x, y], {{x, 0.0}, {y, 0.0}}]
Out[1]=

Visualize the Rosenbrock function and show the location of its minimum value:

In[2]:=
ContourPlot[ ResourceFunction["RosenbrockFunction"][x, y], {x, -2, 2}, {y, -1, 3}, Contours -> 100, Epilog -> {Orange, AbsolutePointSize[5], Point[{1, 1}]}]
Out[2]=

Scope (2) 

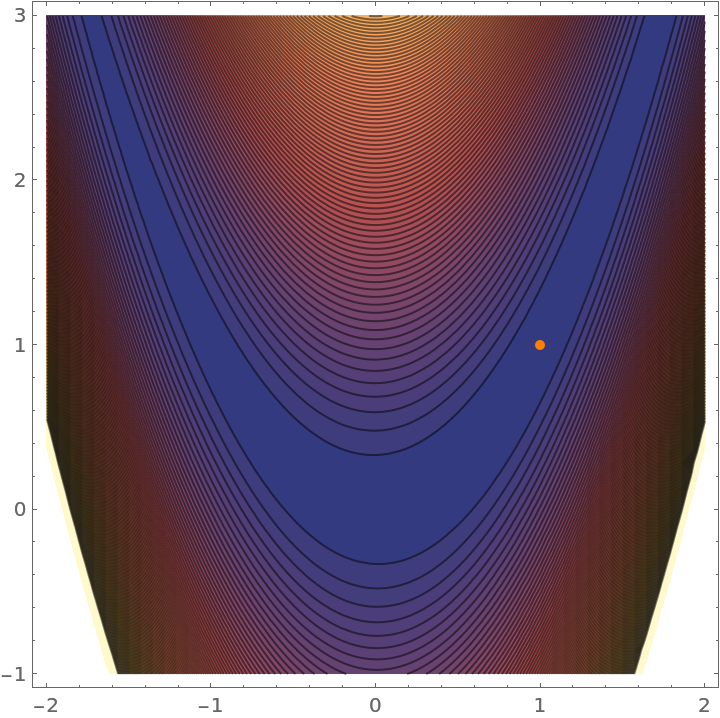Compute the gradient:

In[3]:=
gradient = Grad[ResourceFunction["RosenbrockFunction"][x, y], {x, y}]
Out[3]=

Make a vector plot of the gradient:

In[4]:=
VectorPlot[gradient, {x, -2, 2}, {y, -1, 3}]
Out[4]=

Publisher

WolframExternalFunctions

Requirements

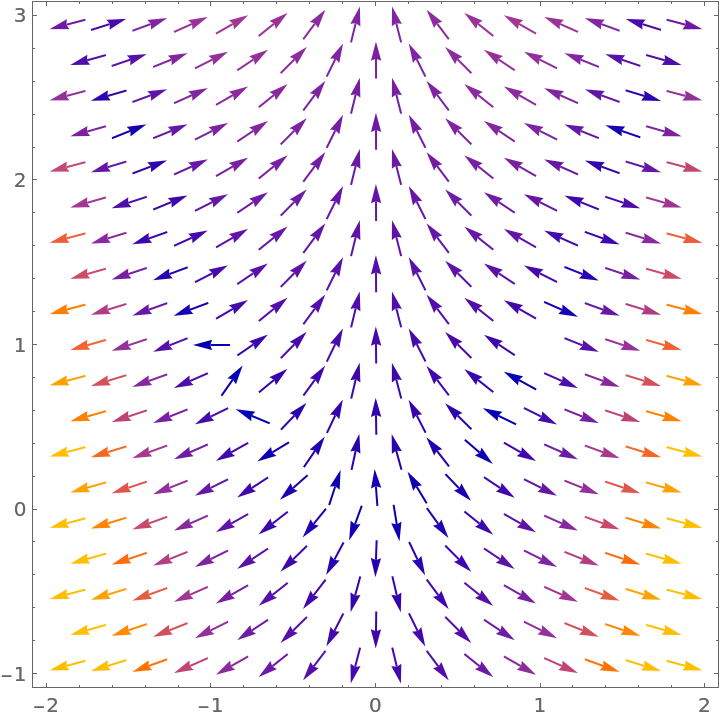Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 22 April 2024

License Information