Basic Examples (4)
Find a sequence which converges to the same limit faster than the input sequence:
Given the first few terms of a sequence, find terms of another sequence with accelerated convergence:
Accelerate the convergence of the sequence 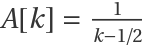 by specifying the auxiliary sequences:
by specifying the auxiliary sequences:
Give a finite list and specify auxiliary lists:
Options (5)
Method (3)
The default Method is "BrezinskiE", which uses a recursive definition:
The Method "Cramer" calculates determinants:
Use "LinearSolve":
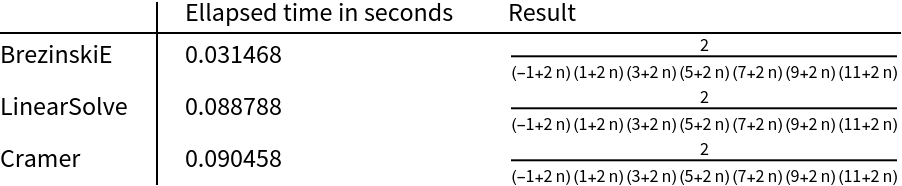
Compare the method outputs in a table:
They are all equivalent:
"BrezinskiE" is generally faster than the "LinearSolve" and "Cramer" methods for sequences and lists:
"BrezinskiE" and "LinearSolve" perform similarly on lists, while the "Cramer" Method is slower:
MinWorkingPrecision (2)
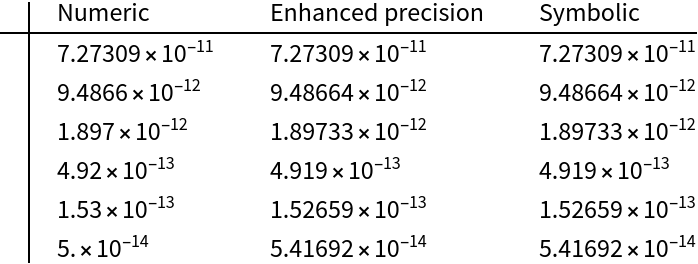
Set "MinWorkingPrecision", which applies SetPrecision on entries that have smaller Precision than the specified value:
In numeric calculations, the "Cramer" Method preserves higher Precision:
Applications (6)
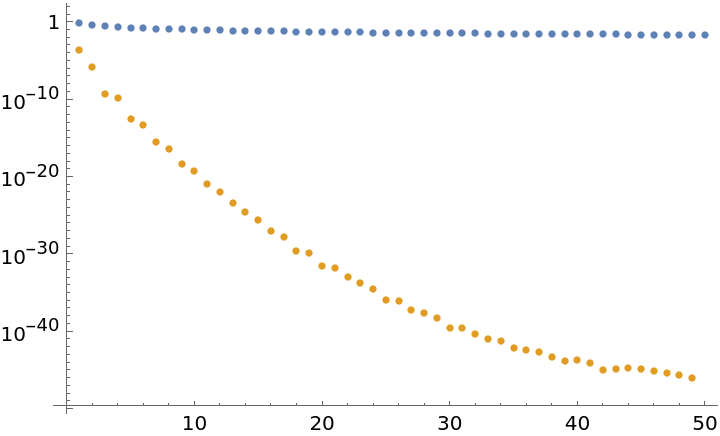
Calculate the convergence of the Basel series:
Accelerate the convergence with RichardsonExtrapolate and plot a comparison:
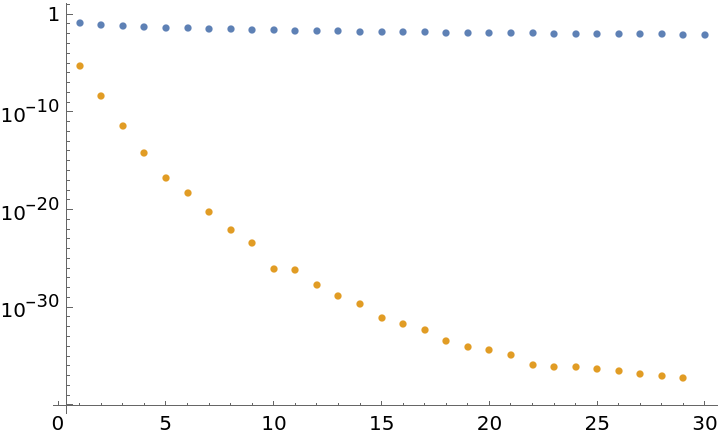
Calculate the convergence of the Leibniz formula for 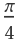 :
:
Accelerate the convergence and plot a comparison:
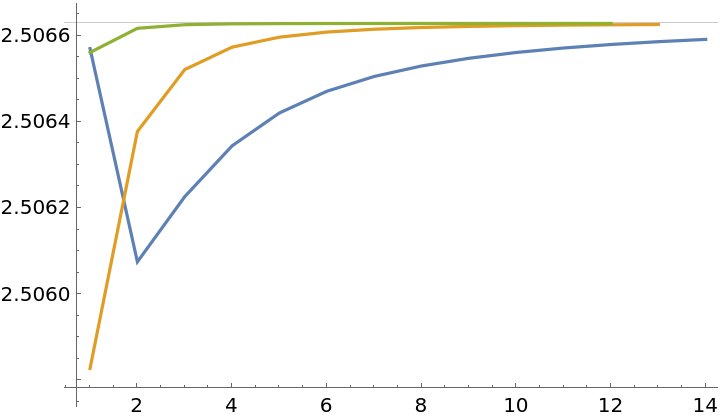
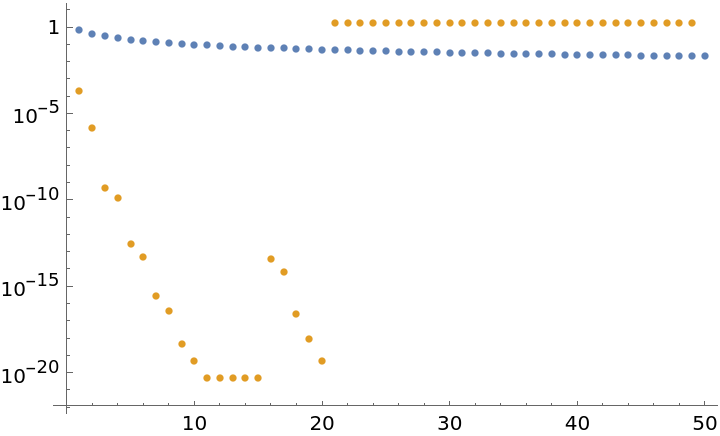
Calculate the convergence of Stirling's formula:
Numerically verify the convergence using different orders:
Numerically approximate the Zeta[1.2] function:
Use RichardsonExtrapolate with different orders to attempt to accelerate the convergence:
Plot a comparison when the sequence has more terms:
Compute 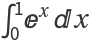 :
:
Accelerate a (left) Riemann sum approximating 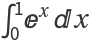 :
:
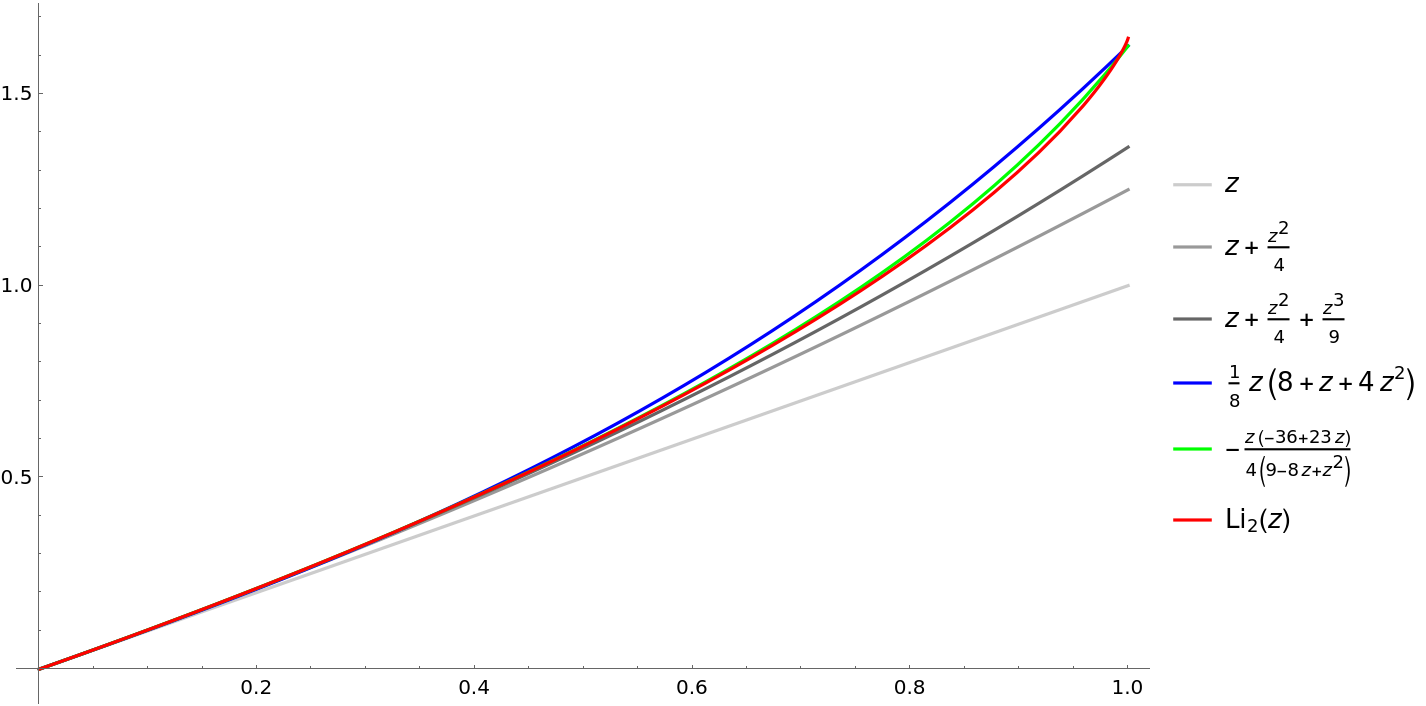
Approximate the PolyLog[2,z] function from only 3 terms in its Taylor expansion:
Use an auxiliary sequence:
Compare the approximations with the original function in a plot:
Properties and Relations (5)
RichardsonExtrapolate is linear:
RichardsonExtrapolate reduces the length of a List:
If a sequence a[k] is convergent, then a[k] and its transformed version both converge to the same limit:
RichardsonExtrapolate can accelerate the convergence of logarithmic sequences:
RichardsonExtrapolate can eliminate series coefficients from the asymptotic expansion of a sequence:
Possible Issues (2)
A failure to find the appropriate auxiliary sequence can cause divergent behavior:
Use an appropriate auxiliary sequence:
Numeric errors can have a dramatic effect on the results:
Neat Examples (2)
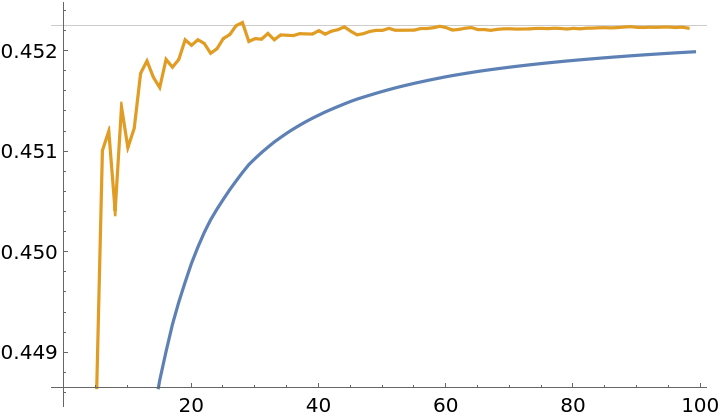
Consider the PrimeZetaP[2] partial sums:
Approximate with RichardsonExtrapolate and compare the results:
Compare the limits in a table:
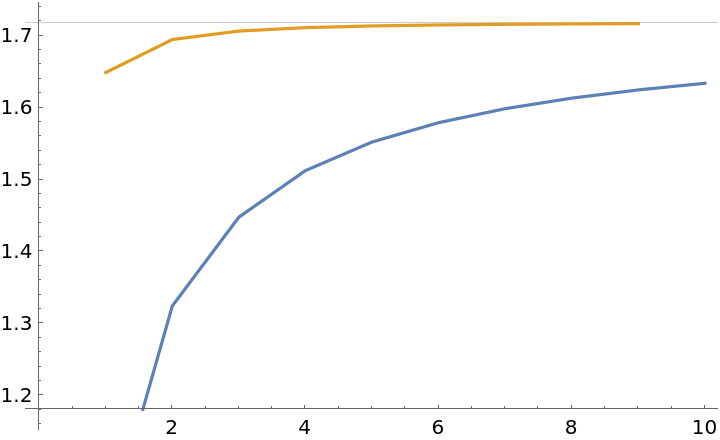
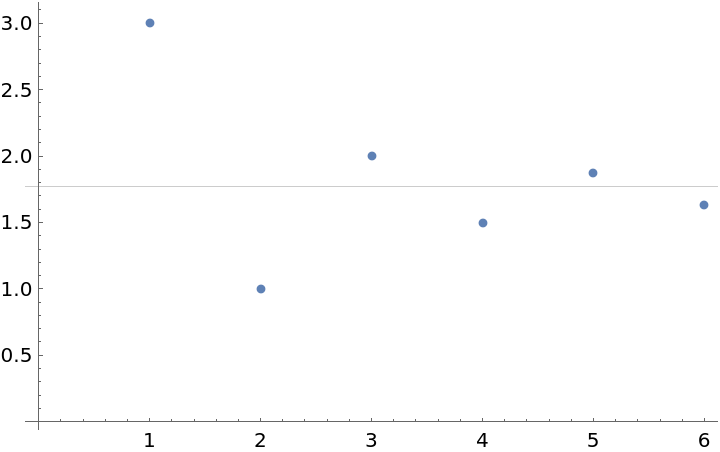
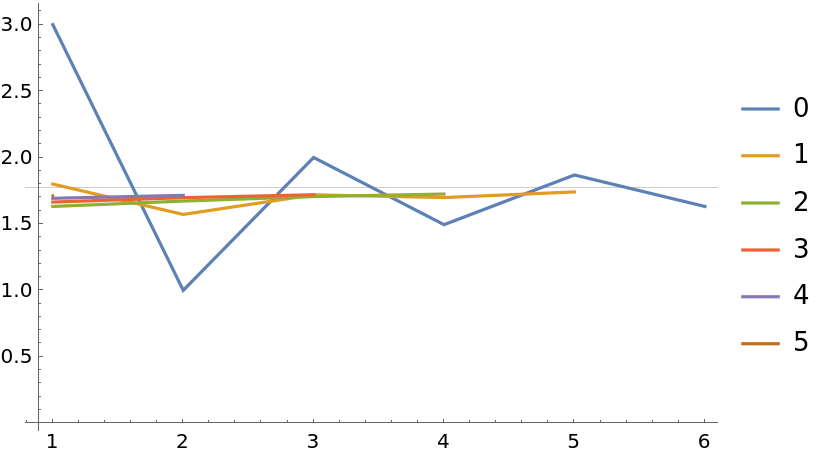
Approximate the Eigenvalues of an operator by a sequence of truncated matrix representations:
Accelerate the convergence using RichardsonExtrapolate:
Approximating the ground state of the antiferromagnetic Heisenberg spin chain (4)
Construct the Hamiltonian of the model, which is a 2n×2n dimensional matrix, where n is the length of the spin chain:
Calculate the ground state energy density by exact diagonalization:
Use Richardson Extrapolation to estimate the thermodynamic limit as n→∞:
Compare the results with the exact ground state:
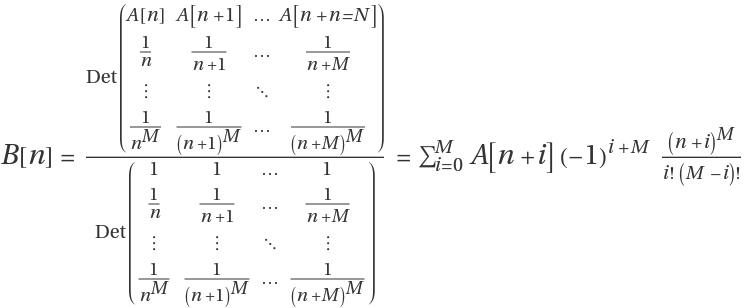

![]() by specifying the auxiliary sequences:
by specifying the auxiliary sequences: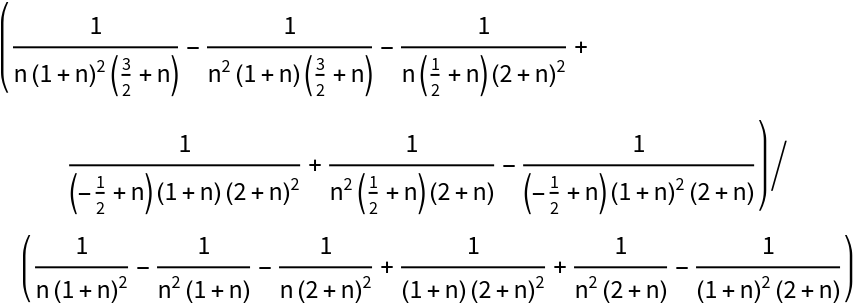

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/f6595b1c-8861-42eb-bcc0-32b9b5d135ba"]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/6c315d98942d9fd0.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4ca3f3d7-af14-4624-ad11-6409f9c1cf36"]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/7164459af9934b62.png)

![data1 = Table[1/(2 k + 1), {k, 1, 15}];
data2 = Table[1.`20/(2 k + 1), {k, 1, 15}];](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/37575be5f5f30757.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1507b8cb-95d3-4d5d-993c-5777e2065628"]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/53e8676e4b5e5f6b.png)
![data1 = Table[1.`50/(2 k + 1), {k, 1, 30}];
data2 = Table[1/(2 k + 1), {k, 1, 30}];](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/2de1e5b497980643.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/19816bf2-ff3f-4c40-ae4e-38ac07c750e0"]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/75d6d37c24ad07b7.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1492ad4f-ba70-48e8-888a-9de81db7be9b"]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/5cfe15738525a8b9.png)

![partialsum = Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(k\)]
\*FractionBox[\(1\),
SuperscriptBox[\(i\), \(2\)]]\), {k, 1, 50}];
accsum = Table[
Last@ResourceFunction["RichardsonExtrapolate"][partialsum, n], {n, 1, 50 - 1}];
ListLogPlot[{Abs[partialsum - \[Pi]^2/6], Abs[accsum - \[Pi]^2/6]}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/2e5dcabc1986b48a.png)
![]() :
:![partialsum = Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 0\), \(k\)]\(
\*SuperscriptBox[\((\(-1\))\), \(i\)]
\*FractionBox[\(1\), \(2 i + 1\)]\)\), {k, 1, 30}];
accsum = Table[
Last@ResourceFunction["RichardsonExtrapolate"][partialsum, Table[Table[1/k^i (-1)^k, {k, 1, 30}], {i, 1, n}]], {n, 1, 30 - 1}];
ListLogPlot[{Abs[partialsum - \[Pi]/4], Abs[accsum - \[Pi]/4]}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/2582b9cc3fcb1641.png)
![ListLinePlot[
Table[ResourceFunction["RichardsonExtrapolate"][
Table[n!/(\[Sqrt]n n^n E^-n), {n, 1, 15}], M], {M, 1, 3}], PlotRange -> All, GridLines -> {{}, {Sqrt[2 \[Pi]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/157008e723b971eb.png)
![partialsum = Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(k\)]
\*FractionBox[\(1\),
SuperscriptBox[\(i\), \(1.2`20\)]]\), {k, 1, 8}];
accsumlist = Table[ResourceFunction["RichardsonExtrapolate"][partialsum, Table[1/k^(0.2`20 + i), {i, 0, M - 1}, {k, 1, 8}]], {M, 1, 6}];
TableForm[accsumlist, TableHeadings -> {{"M=1", "M=2", "M=3", "M=4", "M=5", "M=6"}, {}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/337bcf97c9829688.png)

![partialsum = Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(k\)]
\*FractionBox[\(1\),
SuperscriptBox[\(i\), \(1.2`120\)]]\), {k, 1, 50}];
accsum = Table[
ResourceFunction["RichardsonExtrapolate"][partialsum, Table[Table[1/k^(0.2`120 + i), {k, 1, 50}], {i, 0, M - 1}]] // Last, {M, 1, 50 - 1}];
ListLogPlot[Abs[accsum - Zeta[1.2`120]], PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/6e8b22ee87dd5183.png)

![]() :
:![]() :
:
![Plot[{taylorpoly, accpoly, accpoly2, PolyLog[2, z]}, {z, 0, 1},
PlotStyle -> {GrayLevel[0.8], GrayLevel[0.6], GrayLevel[0.4], Blue, Green, Red},
PlotLegends -> "Expressions",
ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/4163bf860b7fd754.png)
![ResourceFunction[
"RichardsonExtrapolate"][\[Alpha] a[k] + \[Beta] b[k], 1, k, n] == \[Alpha] ResourceFunction["RichardsonExtrapolate"][a[k], 1, k,
n] + \[Beta] ResourceFunction["RichardsonExtrapolate"][b[k], 1, k, n]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/1b92480152cea980.png)
![length = 10;
M = 3;
ResourceFunction["RichardsonExtrapolate"][
Table[1/(2 k + 1), {k, 1, length}], M]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/4aefd195215271db.png)
![partialsum = N[Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(k\)]
\*FractionBox[\(1\),
SuperscriptBox[\(i\), \(2\)]]\), {k, 1, 50}], 20];
accsum = Table[
Last@ResourceFunction["RichardsonExtrapolate"][partialsum, n], {n, 1, 50 - 1}];
ListLogPlot[{Abs[partialsum - \[Pi]^2/6], Abs[SetPrecision[accsum, 50] - \[Pi]^2/6]}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/1d2813a76a0dcdfa.png)
![partialsum = Table[Sum[1/Prime[k]^2, {k, 1, n}], {n, 2, 100}];
accsum = ResourceFunction["RichardsonExtrapolate"][
partialsum, {Table[1/(k Log[k]^2), {k, 2, 100}]}];
ListLinePlot[{partialsum, accsum}, GridLines -> {{}, {PrimeZetaP[2]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/1fe0834d487a3f0c.png)
![TableForm[{PrimeZetaP[2], partialsum // Last, accsum // Last} // N, TableHeadings -> {{"P(2)", "\!\(\*SuperscriptBox[\(100\), \(th\)]\) partial sum of \!\(\*FractionBox[\(1\), SuperscriptBox[SubscriptBox[\(p\), \(k\)], \(2\)]]\)", "Richardson Estrapolation"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/2e2ae1d7d713d154.png)
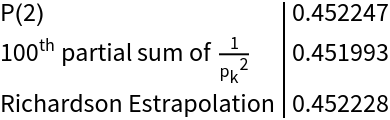

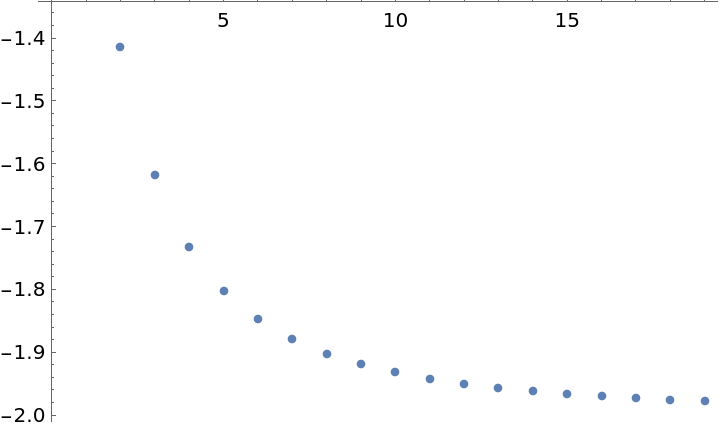
![ListLinePlot[{groundstatesequence, ResourceFunction["RichardsonExtrapolate"][groundstatesequence, 1], ResourceFunction["RichardsonExtrapolate"][groundstatesequence, 2]}, GridLines -> {{}, {-2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/2a7d048953ae2666.png)
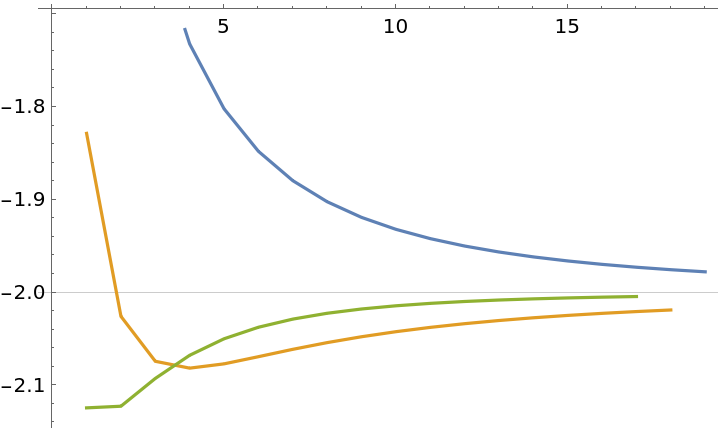
![nMax = 7;
ListPlot[eList = Table[(Eigenvalues[N[H[n]]] // Sort // Last)/n, {n, 2, nMax}], GridLines -> {{}, {-1 + 4 Log[2]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/6e27977b3044a7ba.png)
![MMax = 5;
ListLinePlot[
Table[ResourceFunction["RichardsonExtrapolate"][eList, Evaluate[Table[Table[(-1)^n/n^i, {n, 2, nMax}], {i, 1, M}]]], {M, 0, MMax}], GridLines -> {{}, {-1 + 4 Log[2]}}, PlotRange -> All, PlotLegends -> Range[0, 5]]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/5656e6bb3761483a.png)
![TableForm[
Table[ResourceFunction["RichardsonExtrapolate"][eList, Evaluate[Table[Table[(-1)^n/n^i, {n, 2, nMax}], {i, 1, M}]]], {M, 0, MMax}], TableHeadings -> {{"M=0", "M=1", "M=2", "M=3", "M=4", "M=5"}, {"n=2",
"n=3", "n=4", "n=5", "n=6", "n=7"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/7c6eac78f3e26801.png)

![TableForm[
Table[Abs[# - eExact] & /@ ResourceFunction["RichardsonExtrapolate"][eList, Evaluate[Table[Table[(-1)^n/n^i, {n, 2, nMax}], {i, 1, M}]]], {M, 0, MMax}], TableHeadings -> {{"M=0", "M=1", "M=2", "M=3", "M=4", "M=5"}, {"n=2",
"n=3", "n=4", "n=5", "n=6", "n=7"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee1/ee14a2f5-b1f4-44f8-9c83-bc90a63310ff/6955da0bf13ad576.png)
