Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RicciScalar

Source Notebook

Compute the Ricci scalar for a metric

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["RicciScalar"][M,{u,v}]

computes the Ricci scalar for a metric M in terms of variables u and v.

Details and Options

The scalar curvature is the contraction of the Ricci tensor, and is written as R without subscripts or arguments: .
The Ricci scalar curvature has a meaning very similar to the Gaussian curvature.

Examples

Basic Examples (2) 

The monkey saddle surface:

In[1]:=
monkeysaddle[u_, v_] := {u, v, u^3 - 3 u v^2}
In[2]:=
ms = monkeysaddle[u, v]
Out[2]=

Plot the surface:

In[3]:=
ParametricPlot3D[{u, v, u^3 - 3 u v^2}, {u, -\[Pi], \[Pi]}, {v, -\[Pi], \[Pi]}, BoxRatios -> {1, 1, 1}, PlotRange -> All]
Out[3]=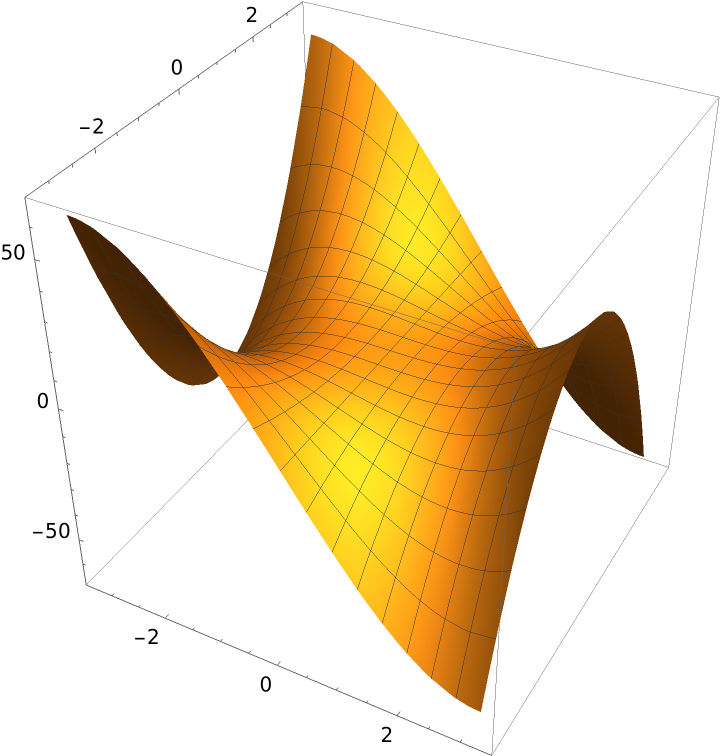

The covariant basis:

In[4]:=
{Subscript[g, \[Alpha]], Subscript[g, \[Beta]]} = Transpose@(D[{u, v, u^3 - 3 u v^2}, {{u, v}}])
Out[4]=

The metric tensor:

In[5]:=
Subscript[g, \[Alpha]\[Beta]] = SymmetrizedArray[{{1, 1} -> Subscript[g, \[Alpha]] . Subscript[g, \[Alpha]], {1, 2} -> Subscript[g, \[Alpha]] . Subscript[g, \[Beta]], {2, 2} -> Subscript[g, \[Beta]] . Subscript[g, \[Beta]]}, {2, 2}, Symmetric[{1, 2}]] // Simplify
Out[5]=

The metric tensor in normal form:

In[6]:=
Subscript[g, \[Alpha]\[Beta]] // Normal
Out[6]=

Compute the Ricci scalar from the metric:

In[7]:=
R = ResourceFunction["RicciScalar"][Subscript[ g, \[Alpha]\[Beta]], {u, v}] // FullSimplify
Out[7]=

Alternately, compute the Ricci scalar via the Ricci curvature:

In[8]:=
rc = ResourceFunction["ArrayContract"][ ResourceFunction["RiemannTensor"][Subscript[ g, \[Alpha]\[Beta]], {u, v}], {{1, 3}}] // FullSimplify
Out[8]=

Contracting an index gives the Ricci scalar:

In[9]:=
ResourceFunction["ArrayContract"][ rc . Inverse[Subscript[g, \[Alpha]\[Beta]]], {{1, 2}}] // FullSimplify
Out[9]=

Confirm that this is equivalent to the Ricci curvature computed previously from the metric directly:

In[10]:=
R - %
Out[10]=

The metric tensor for an arbitrary metric:

In[11]:=
Subscript[g, \[Alpha]\[Beta]] = SymmetrizedArray[{{1, 1} -> e[u, v], {1, 2} -> f[u, v], {2, 2} -> g[u, v]}, {2, 2}, Symmetric[{1, 2}]] // Simplify
Out[11]=

The Brioschi formula for the Gaussian curvature:

In[12]:=
BrioschiCurvature[M_, {u_, v_}] := Module[{U, V, A, B, ee, ff, gg}, ee = M[[1, 1]]; ff = M[[1, 2]]; gg = M[[2, 2]]; A1 = {-\!\( \*SubscriptBox[\(\[PartialD]\), \(v, v\)]ee\) + 2 \!\( \*SubscriptBox[\(\[PartialD]\), \(u, v\)]ff\) - \!\( \*SubscriptBox[\(\[PartialD]\), \(u, u\)]gg\), \!\( \*SubscriptBox[\(\[PartialD]\), \(u\)]ee\), 2 \!\( \*SubscriptBox[\(\[PartialD]\), \(u\)]ff\) - \!\( \*SubscriptBox[\(\[PartialD]\), \(v\)]ee\)}; A2 = {\!\( \*SubscriptBox[\(\[PartialD]\), \(v\)]ff\) - \!\( \*SubscriptBox[\(\[PartialD]\), \(u\)]gg\)/2, ee, ff}; A3 = {\!\( \*SubscriptBox[\(\[PartialD]\), \(v\)]gg\)/2, ff, gg}; A = {A1/2, A2, A3}; B1 = {0, \!\( \*SubscriptBox[\(\[PartialD]\), \(v\)]ee\), \!\( \*SubscriptBox[\(\[PartialD]\), \(u\)]gg\)}; B2 = {\!\( \*SubscriptBox[\(\[PartialD]\), \(v\)]ee\)/2, ee, ff}; B3 = {\!\( \*SubscriptBox[\(\[PartialD]\), \(u\)]gg\)/2, ff, gg}; B = {B1/2, B2, B3}; AB = (Det[A] - Det[B])/Det[M]^2; Simplify[AB]]

Compute the Ricci scalar for the arbitrary metric:

In[13]:=
ResourceFunction["RicciScalar"][Subscript[ g, \[Alpha]\[Beta]], {u, v}] // FullSimplify
Out[13]=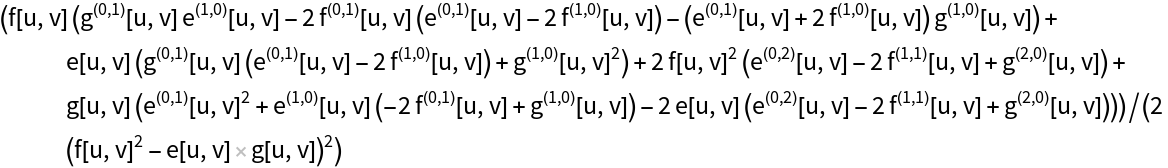

Prove that this coincides with twice the Gaussian curvature:

In[14]:=
% - 2 BrioschiCurvature[Subscript[ g, \[Alpha]\[Beta]], {u, v}] // FullSimplify
Out[14]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 24 November 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.
    • Loveridge, L. C., "Physical and Geometric Interpretations of the Riemann Tensor, Ricci Tensor, and Scalar Curvature." arXiv Preprint, 2004. https://arxiv.org/abs/gr-qc/0401099

Related Resources

License Information