Author Notes
Ideas for future research including adding support for different distance functions including “Boundary”, corresponding to minimum distance between any points in regions, and “SignedBoundary”, corresponding to distance to boundary, negative for interior points. I think “Center” is used by default, which corresponds to distance between centers of regions. I tried using RegionDistance which as of 13.3 supports region1 and region2, not just a region and a point, but the problem was what function it was using to compute the distance. I think it was using the geodesic distance over the ellipsoid. The problem was that it differed slightly from GeoDistance for some reason.
GeoDistance[,,DistanceFunction→"Boundary"] () should be equivalent to Quantity[RegionDistance[Region[["Polygon"]],Region[["Polygon"]]],"Meters"] (). The difference is . To make this work, I would need to first figure out why there is a difference here. Then I would need indicate to RegionDistance I am using not the geodesic distance but the loxodromic distance. The function SignedRegionDistance could be used for the option "SignedBoundary" once it supports two regions, and not just a region and a point. SignedRegionDistanceis effectivelyMinValue[{Norm[p-q],q∈reg},q∈reg]whenpis not inregand-MinValue[{Norm[p-q],q∉reg},q]otherwise. This could be used to compute the signed region distance while I wait for support for two regions to be introduced, but there's still the bug and the problem of using a loxodrome and not a geodesic. An example of where this could be useful is GeoDistance[,] () and GeoDistance[,,DistanceFunction→"SignedBoundary"] ().
![ResourceFunction[
"RhumbLineDistanceList"][{Entity[
"City", {"BuenosAires", "BuenosAires", "Argentina"}], Entity["City", {"RioDeJaneiro", "RioDeJaneiro", "Brazil"}], Entity["City", {"MexicoCity", "DistritoFederal", "Mexico"}], Entity["City", {"NewYork", "NewYork", "UnitedStates"}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/686/686b962d-58de-4d92-8c4b-2586ec03a01a/18ceb28682e29499.png)
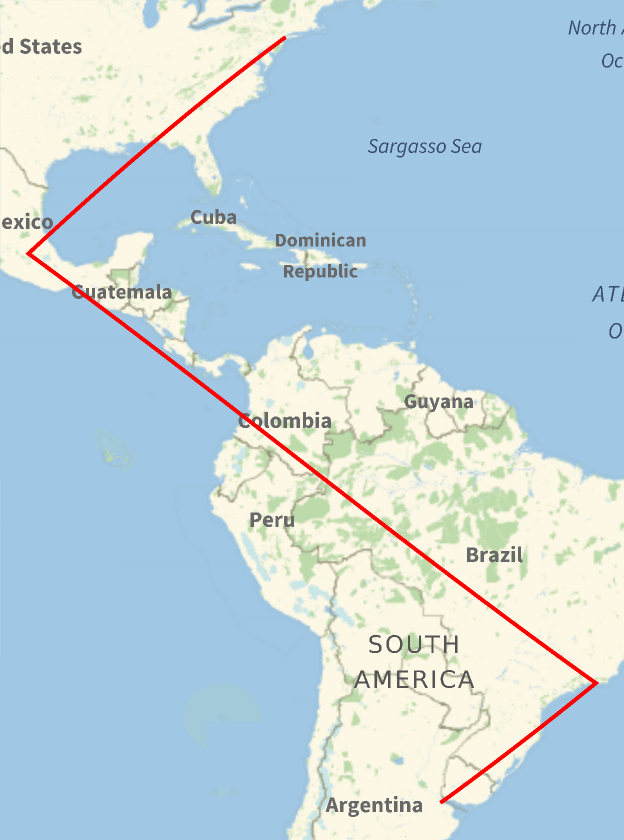
![GeoGraphics[{Red, Thick, GeoPath[{Entity[
"City", {"BuenosAires", "BuenosAires", "Argentina"}], Entity["City", {"RioDeJaneiro", "RioDeJaneiro", "Brazil"}], Entity["City", {"MexicoCity", "DistritoFederal", "Mexico"}], Entity["City", {"NewYork", "NewYork", "UnitedStates"}]}, "RhumbLine"]}]](https://www.wolframcloud.com/obj/resourcesystem/images/686/686b962d-58de-4d92-8c4b-2586ec03a01a/0acbbec5106ce2fb.png)
![ResourceFunction[
"RhumbLineDistanceList"][{{"46°25'12''N", "21°1'12''W"}, {"30°13'48.''S", "40°30'36.''E"}, {"40d20m12s N", "112d50m W"}}] // Normal](https://www.wolframcloud.com/obj/resourcesystem/images/686/686b962d-58de-4d92-8c4b-2586ec03a01a/27804591ac930205.png)
![GeoDistanceList[{Entity[
"City", {"SanFrancisco", "California", "UnitedStates"}], Entity["City", {"Chicago", "Illinois", "UnitedStates"}], Entity["City", {"NewYork", "NewYork", "UnitedStates"}]}, UnitSystem -> "Imperial"] // Normal](https://www.wolframcloud.com/obj/resourcesystem/images/686/686b962d-58de-4d92-8c4b-2586ec03a01a/33b954a23daf9989.png)
![ResourceFunction[
ResourceObject[<|"Name" -> "GeoSpatialDistanceList", "ShortName" -> "GeoSpatialDistanceList", "UUID" -> "eceee46d-d7cb-4d22-9623-4ab8b817384e", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Get a list of spatial distances between consecutive pairs of locations", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$f5baab64247d4d429cefa66b4103a61f`GeoSpatialDistanceList", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/f8a79128-8295-4c52-be61-e112e831c145"]|>, ResourceSystemBase -> Automatic]][
GeoPosition /@ {Entity[
"City", {"SanFrancisco", "California", "UnitedStates"}], Entity["City", {"Chicago", "Illinois", "UnitedStates"}], Entity["City", {"NewYork", "NewYork", "UnitedStates"}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/686/686b962d-58de-4d92-8c4b-2586ec03a01a/01717847d6c2d6fb.png)

