Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ReuleauxPolygon

Source Notebook

Represent a Reuleaux polygon

Contributed by: Jan Mangaldan

ResourceFunction["ReuleauxPolygon"][n]

gives the Reuleaux polygon constructed from n vertices equally spaced around the unit circle.

ResourceFunction["ReuleauxPolygon"][r,n]

gives the Reuleaux polygon based on a regular polygon of radius r.

ResourceFunction["ReuleauxPolygon"][{r,θ},n]

starts at angle θ with respect to the x axis.

ResourceFunction["ReuleauxPolygon"][{x,y},rspec,n]

centers the Reuleaux polygon at {x,y}.

Details

A Reuleaux polygon is a polygon of constant width made up of circular arcs of constant radius.
n must be a positive odd integer.
The angle θ is measured in radians counterclockwise from the positive x-direction.
ResourceFunction["ReuleauxPolygon"] returns a FilledCurve object and can be used as a graphics primitive.

Examples

Basic Examples (2) 

A Reuleaux triangle:

In[1]:=
Graphics[ResourceFunction["ReuleauxPolygon"][3]]
Out[1]=

Different styles applied to ReuleauxPolygon:

In[2]:=
\[ScriptCapitalR] = ResourceFunction["ReuleauxPolygon"][7]; {Graphics[{Pink, \[ScriptCapitalR]}], Graphics[{EdgeForm[Thick], Pink, \[ScriptCapitalR]}], Graphics[{EdgeForm[Dashed], Pink, \[ScriptCapitalR]}], Graphics[{EdgeForm[Directive[Thick, Dashed, Blue]], Pink, \[ScriptCapitalR]}]}
Out[2]=

Scope (4) 

Generate a Reuleaux triangle, pentagon, heptagon, etc.:

In[3]:=
Table[Graphics[ResourceFunction["ReuleauxPolygon"][n]], {n, 3, 11, 2}]
Out[3]=

Generate Reuleaux pentagons of varying radii:

In[4]:=
rp = Table[ResourceFunction["ReuleauxPolygon"][r, 5], {r, 1, 4}];
In[5]:=
Graphics[{Opacity[0.2], rp}]
Out[5]=

Generate Reuleaux triangles of varying starting angles:

In[6]:=
rp = Table[ ResourceFunction["ReuleauxPolygon"][{1, t Pi/6}, 3], {t, 4}];
In[7]:=
Graphics[{Opacity[0.2], rp}]
Out[7]=

FaceForm and EdgeForm can be used to specify the styles of the interior and boundary:

In[8]:=
Graphics[{FaceForm[Pink], EdgeForm[Directive[Dashed, Thick, Blue]], ResourceFunction["ReuleauxPolygon"][7]}]
Out[8]=

Properties and Relations (1) 

ReuleauxPolygon uses the same vertices as RegularPolygon:

In[9]:=
Table[Graphics[{FaceForm[], {EdgeForm[Blue], RegularPolygon[n]}, {EdgeForm[Red], ResourceFunction["ReuleauxPolygon"][n]}}], {n, 3, 11, 2}]
Out[9]=

Neat Examples (1) 

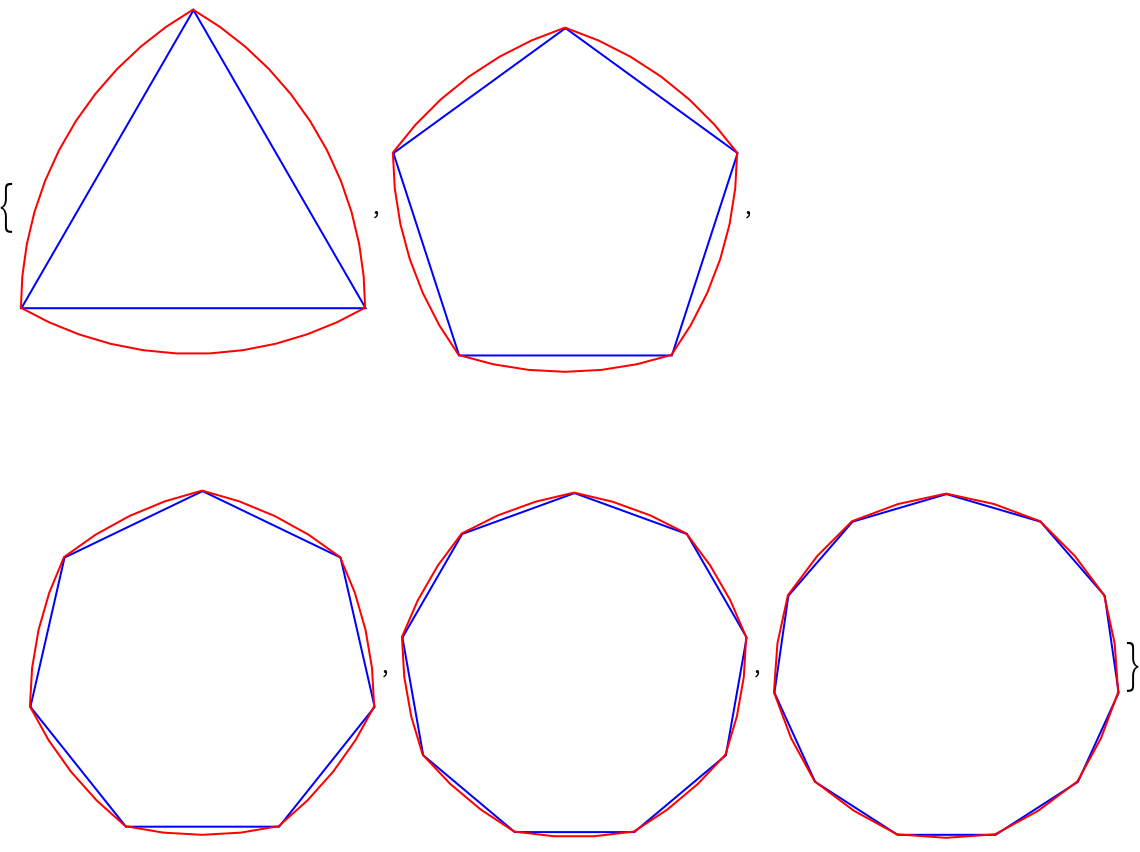A collection of random Reuleaux polygons:

In[10]:=
Graphics[{EdgeForm[Black], Table[{Opacity[0.2], Hue[RandomReal[]], ResourceFunction["ReuleauxPolygon"][ RandomReal[9, 2], {RandomReal[], 0}, 2 RandomInteger[{1, 5}] + 1]}, {200}]}]
Out[10]=

Version History

  • 1.0.0 – 06 December 2021

Related Resources

License Information