Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RelativisticInertialDeformedRegion

Source Notebook

Compute the apparent visual shape of an object or region traveling with constant velocity

Contributed by: Utkarsh Bajaj (Junior Research Affiliate in the Wolfram Physics Project)

ResourceFunction["RelativisticInertialDeformedRegion"][region,speed,tObs,accuracyGoal]

gives the deformed visual shape of region, intially positioned at the origin,traveling at speed along the positive x-axis, at time tObs and with an accuracy of accuracyGoal.

ResourceFunction["RelativisticInertialDeformedRegion"][region,speed,θ,ϕ,tObs,accuracyGoal]

gives the deformed visual shape when region is traveling in the direction defined by spherical coordinates θ and ϕ.

ResourceFunction["RelativisticInertialDeformedRegion"][region,vec,speed,θ,ϕ,tObs,accuracyGoal]

gives the deformed visual shape when region is intially positioned at vec.

Details and Options

The result will be a DiscretizedRegion.
speed should be a number between 0 and 1 (units are set with speed of light c=1).
vec is the initial position of the origin for the moving frame of reference. This function places the stationary observer's reference frame at (0,0,0).
The input region is the actual shape as seen in the moving frame of reference.
The value of accuracyGoal can be set between 0 and ∞. High accuracy goals might not work for some objects.

Examples

Basic Examples (2) 

Compute the apparent shape of a sphere with radius 2 moving with speed 0.9 in the positive x direction, as observed at different times:

In[1]:=
GraphicsRow[ Table[ResourceFunction["RelativisticInertialDeformedRegion"][ Sphere[], 0.9, time, 100], {time, -6, 6, 3}]]
Out[1]=

If we use Graphics3D with visible axes, we can see that the sphere is only stretched or contracted in the x direction:

In[2]:=
Table[Graphics3D[ ResourceFunction["RelativisticInertialDeformedRegion"][Sphere[], 0.9, time, 100], Axes -> True], {time, -6, 6, 3}]

Scope (7) 

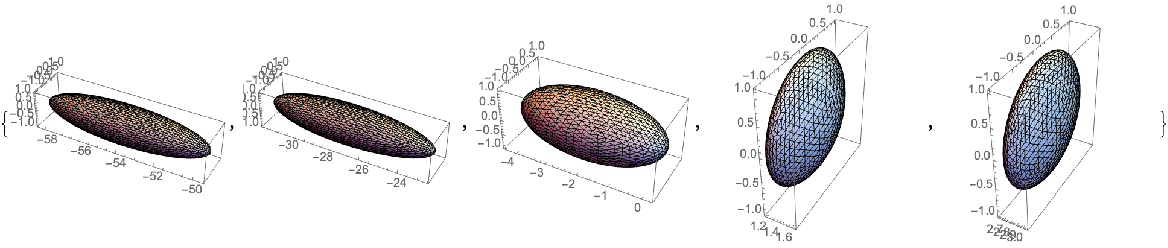
Move the sphere diagonally up and to the right, with a speed of 0.7:

In[3]:=
Graphics3D[ Table[ResourceFunction["RelativisticInertialDeformedRegion"][ Sphere[], 0.7, \[Pi]/2, \[Pi]/2 + \[Pi]/4, time, 100], {time, -6, 6, 3}], Axes -> True]
Out[3]=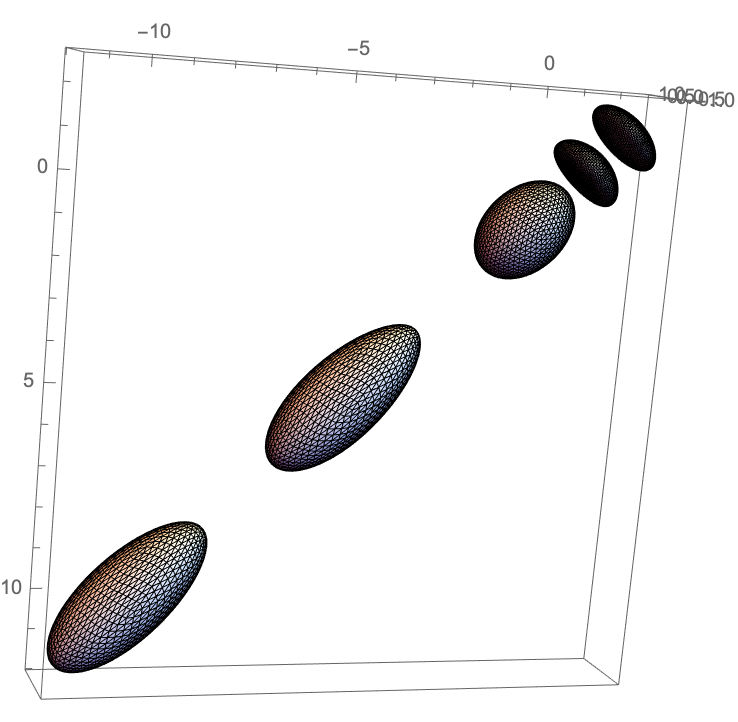

Compute the shape of a sphere centered at (2,2,2) in the moving reference system and moving with a speed of 0.5 in the positive x direction:

In[4]:=
Graphics3D[ ResourceFunction["RelativisticInertialDeformedRegion"][ Sphere[{2, 2, 2}, 2], 0.5, 0, 100], Axes -> True]
Out[4]=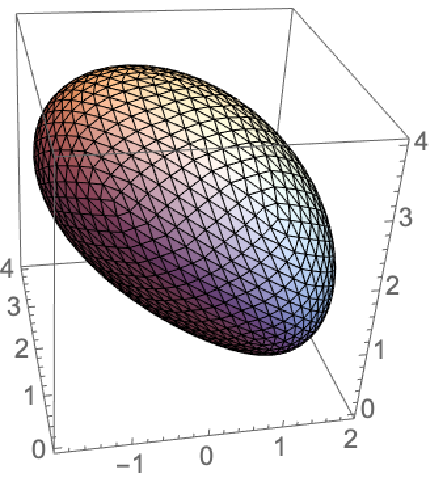

Show the observed shape of a cone initially positioned at (1,1,1), moving at a speed of 0.9 in the positive x direction:

In[5]:=
Graphics3D[ ResourceFunction["RelativisticInertialDeformedRegion"][ Cone[], {1, 1, 1}, 0.9, Pi/2, Pi/2, 0, 1], Axes -> True]
Out[5]=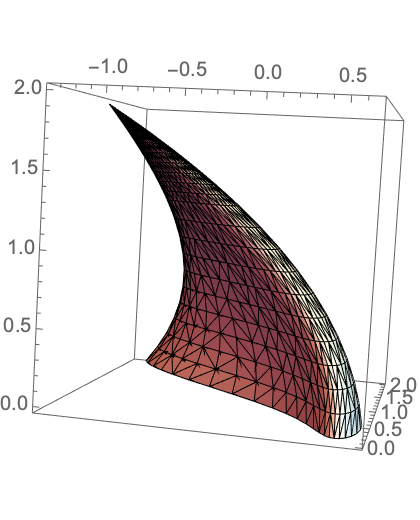

Simulate the visual appearance of different objects when traveling downwards with a speed of 0.95:

In[6]:=
Table[Graphics3D[ ResourceFunction["RelativisticInertialDeformedRegion"][region, 0.95, \[Pi], \[Pi]/2, 0, 2000], Axes -> True], {region, {Cone[], Cube[], ExampleData[{"Geometry3D", "Cow"}, "Region"]}}]

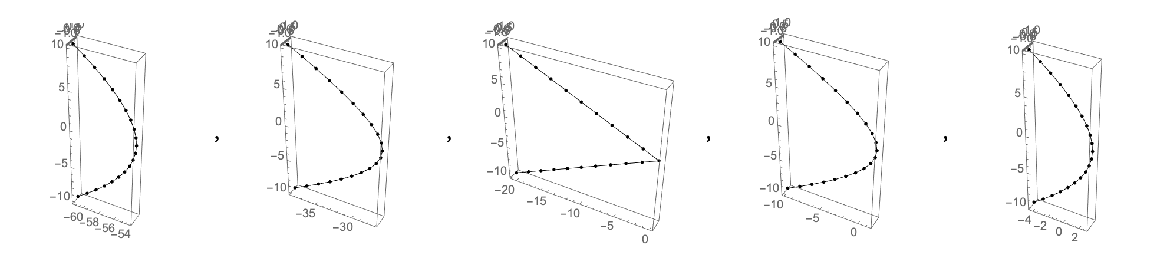
The shape of a vertical line at different times when moving in the x direction is a hyperbola, which degenerates to its asymptotes at time 0:

In[7]:=
Table[Graphics3D[ ResourceFunction["RelativisticInertialDeformedRegion"][ Line[{{0, 0, -10}, {0, 0, 10}}], 0.9, time, 1], Axes -> True], {time, -6, 6, 3}]

Show an icosahedron traveling with different speeds, observed at time 0:

In[8]:=
Table[Graphics3D[ ResourceFunction["RelativisticInertialDeformedRegion"][ Icosahedron[], speed, 0, 3000], Axes -> True], {speed, 0.1, 0.9, 0.2}]
In[9]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/b7526668-6455-4df1-8f27-8f96adca0d52"]

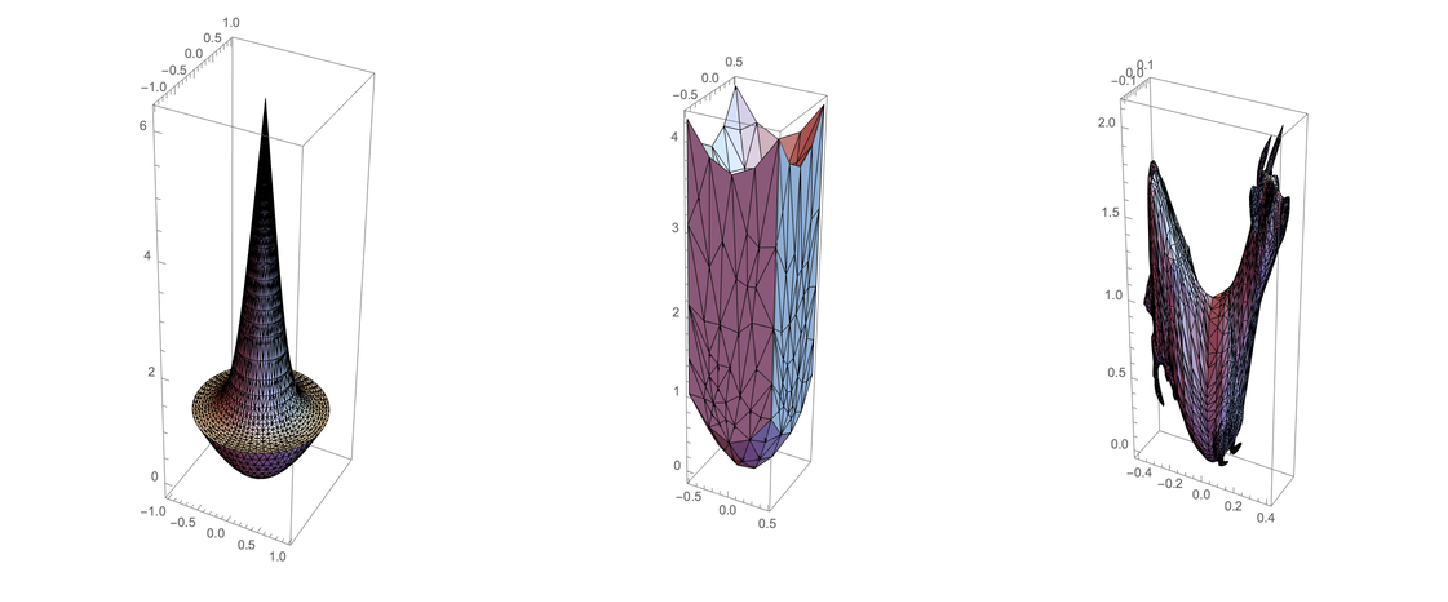
We can also find the apparent shape of an implicit region:

In[10]:=
\[ScriptCapitalR] = ImplicitRegion[ x^6 - 5 x^4 y + 3 x^4 y^2 + 10 x^2 y^3 + 3 x^2 y^4 - y^5 + y^6 + z^2 <= 1, {x, y, z}];

Show the shape of this region traveling upwards with a velocity of 0.8 at different times:

In[11]:=
Graphics3D[ Table[ResourceFunction[ "RelativisticInertialDeformedRegion"][\[ScriptCapitalR], 0.9, 0, \[Pi]/2, time, 100], {time, 0, 10, 3}]]
Out[11]=

Neat Examples (2) 

Show a torus moving at different speeds. Note that the centroid approaches the left edge of the torus as the speed increases:

In[12]:=
Table[Show[ ResourceFunction["RelativisticInertialDeformedRegion"][ ExampleData[{"Geometry3D", "Torus"}, "Region"], speed, 0, 1], Graphics3D[{Red, PointSize[0.1], Point[RegionCentroid[ ResourceFunction["RelativisticInertialDeformedRegion"][ ExampleData[{"Geometry3D", "Torus"}, "Region"], speed, 0, 1]]]}] ], {speed, {0.2, 0.7, 0.9, 0.99, 0.99}}]
Out[12]=

Plot the apparent length of a horizontal line versus time, when moving with a speed of 0.9 along the positive x-axis:

In[13]:=
ListLinePlot[ AssociationThread[Subdivide[-10, 10, 20], Table[ArcLength[ ResourceFunction["RelativisticInertialDeformedRegion"][ Line[{{2, 0, 0}, {-2, 0, 0}}], 0.9, time, 10]], {time, -10, 10, 1}] ] ]
Out[13]=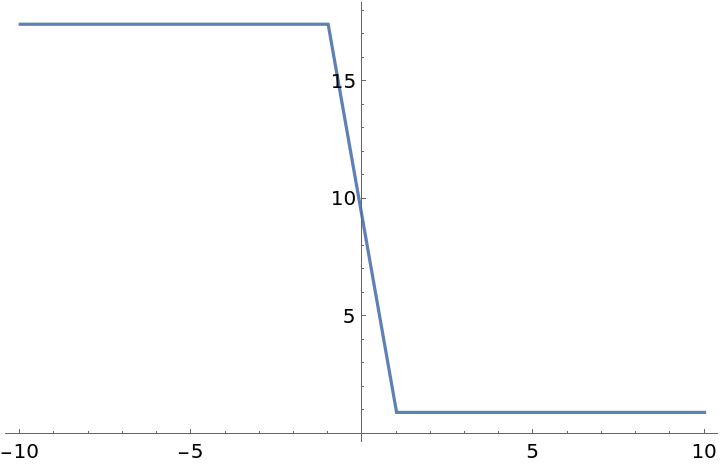

Use a vertical line:

In[14]:=
ListLinePlot[ AssociationThread[Subdivide[-10, 10, 40], Table[ArcLength[ ResourceFunction["RelativisticInertialDeformedRegion"][ Line[{{0, 0, -2}, {0, 0, 2}}], 0.9, time, 10]], {time, -10, 10, 0.5}] ] , PlotRange -> All]
Out[14]=

Possible Issues

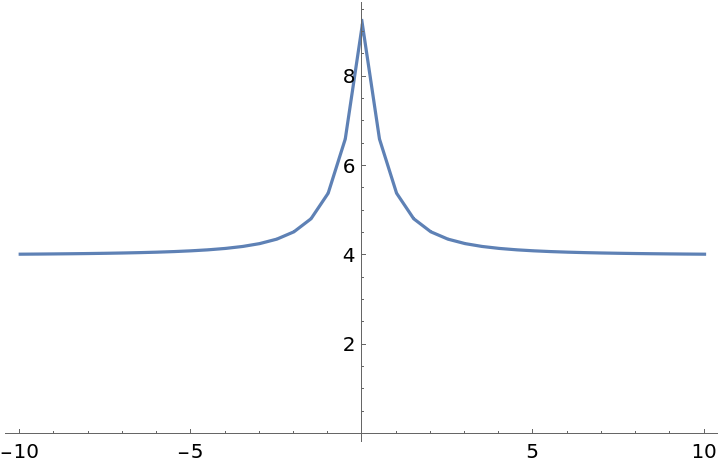For some objects a higher accuracy goal may not work. For example, setting an accuracyGoal above 400 for the Wolfram Spikey leads to Mathematica running the code forever.

Publisher

Wolfram Summer Camp

Version History

  • 1.0.0 – 28 December 2020

Source Metadata

  • Citation:
    T. Muller and S. Boblest. Visual appearance of wireframe objects in special relativity, 2014

Related Resources

Author Notes

If the accuracy goal is too large and the code takes too long to run, the evaluation may be aborted and Mathematica may need to be restarted.

License Information