Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Test whether a graph is reflexive
Tuples form a reflexive graph:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 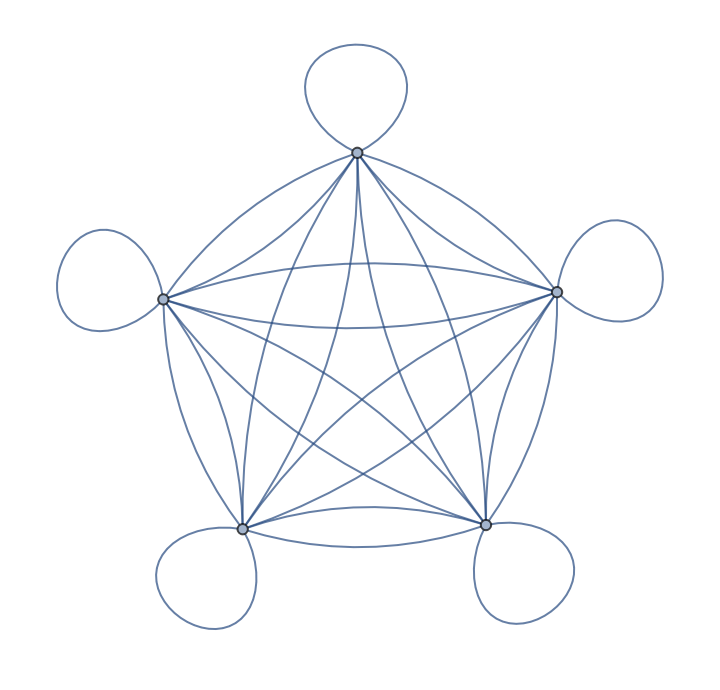 |
| In[3]:= |
| Out[3]= |
After deleting one of its self-loops, the graph is no longer reflexive:
| In[4]:= |
| Out[4]= | 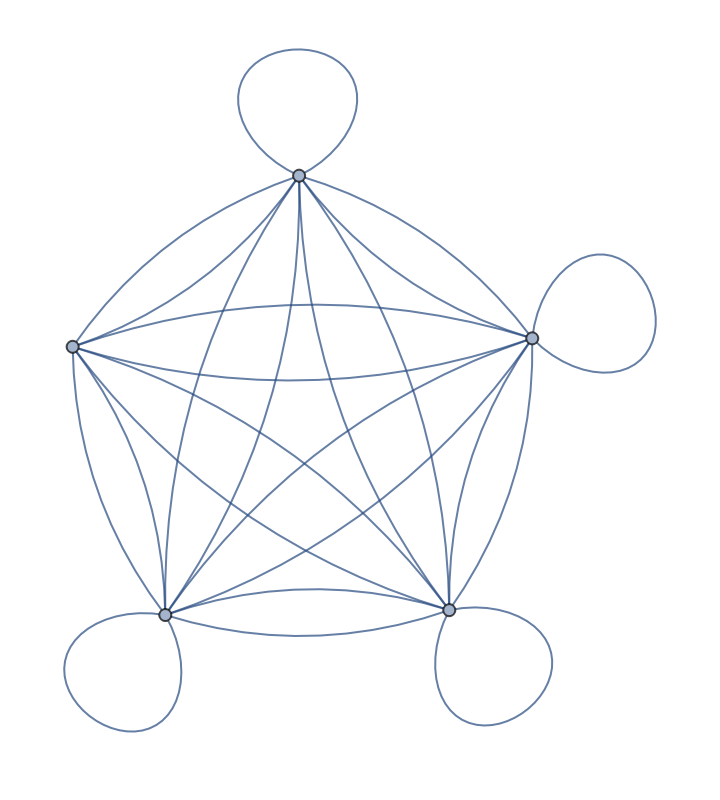 |
| In[5]:= |
| Out[5]= |
The divisibility relation between integers is reflexive since each integer divides itself:
| In[6]:= |
| Out[6]= | 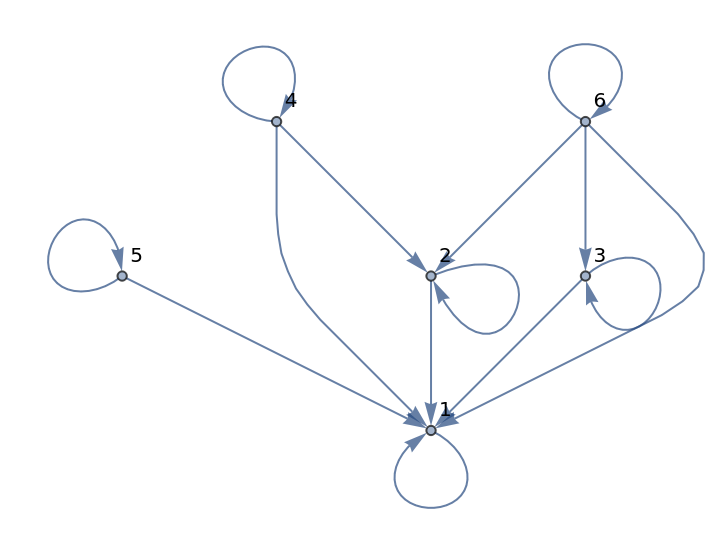 |
| In[7]:= |
| Out[7]= |
This work is licensed under a Creative Commons Attribution 4.0 International License