Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ReflectPoints

Source Notebook

Reflect a set of points over a line, plane or hyperplane defined by points

Contributed by: Ed Pegg Jr and Jan Mangaldan

ResourceFunction["ReflectPoints"][mirror,pts]

reflects pts across mirror.

Details

ResourceFunction["ReflectPoints"] works on points of any dimension.

Examples

Basic Examples (2) 

Reflect points about a given line:

In[1]:=
ref = ResourceFunction["ReflectPoints"][mirror2, pts2]
Out[1]=
In[2]:=
Graphics[{Point[pts2], {Green, InfiniteLine[mirror2]}, {Red, Point[ref]}}]
Out[2]=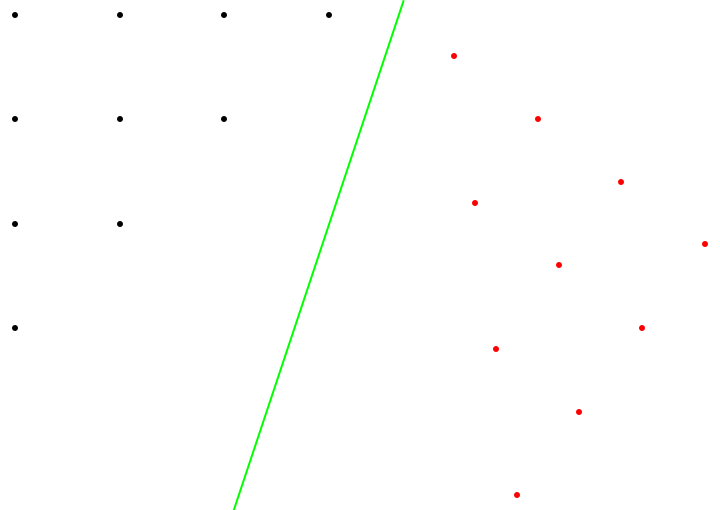

Reflect points about a given plane:

In[3]:=
ref = ResourceFunction["ReflectPoints"][mirror3, pts3]
Out[3]=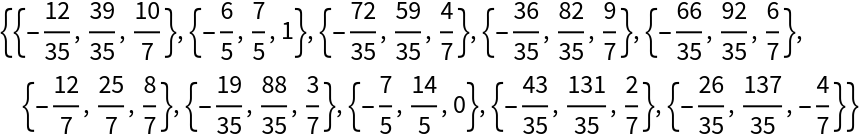
In[4]:=
Graphics3D[{Point[pts3], {Green, InfinitePlane[mirror3]}, {Red, Point[ref]}}, Lighting -> "Standard"]
Out[4]=

Scope (2) 

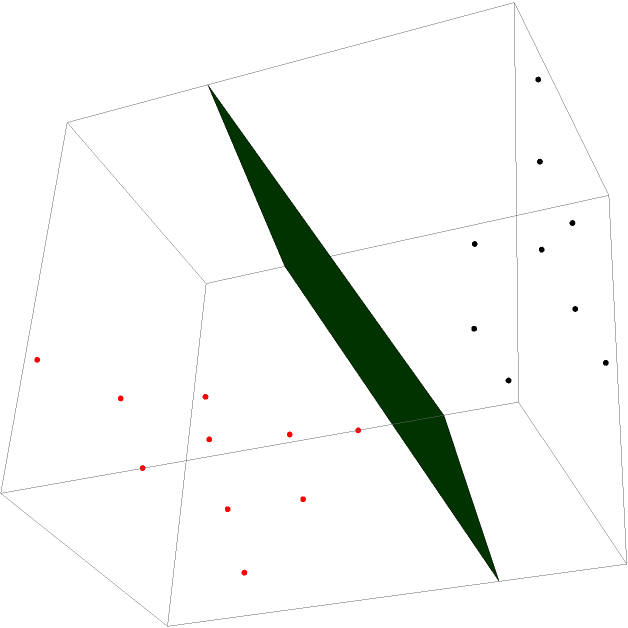Reflect a single point:

In[5]:=
ResourceFunction[ "ReflectPoints"][{{3, 2, 0}, {2, -1, 0}, {1, 1, 1}}, {-1, 4, 7}]
Out[5]=

Generate two sets of random 4D points, one representing a mirror, and the other representing points to transform:

Reflect 4D points about a hyperplane:

In[6]:=
rpts = ResourceFunction["ReflectPoints"][mirror, pts]
Out[6]=

Construct a Hyperplane representation of the mirror:

In[7]:=
hp = Hyperplane[ Cross @@ TranslationTransform[-First[mirror]][Rest[mirror]], First[mirror]]
Out[7]=

Show that the distance between the points and their corresponding reflections is equal to the sum of their distances from the reflecting hyperplane:

In[8]:=
MapThread[ EuclideanDistance, {pts, rpts}] - (RegionDistance[hp, pts] + RegionDistance[hp, rpts]) // Chop
Out[8]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.1.0 – 22 August 2022
  • 1.0.1 – 31 January 2022
  • 1.0.0 – 11 February 2019

License Information