Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the reference angle to a given input angle
ResourceFunction["ReferenceAngle"][θ] gives the reference angle to the angle θ. |
Compute a reference angle:
| In[1]:= |
| Out[1]= |
Compute the reference angle for angles lying in each of the four quadrants:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
Plot the reference angle function for all angles between 0 and 2π:
| In[4]:= |
| Out[4]= | 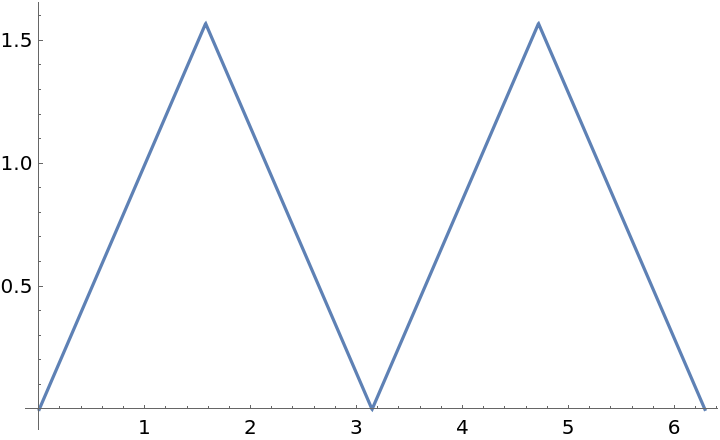 |
ReferenceAngle works directly on Quantity expressions with units of "Radians":
| In[5]:= |
| Out[5]= |
ReferenceAngle will remain unevaluated for non-numeric input:
| In[6]:= |
| Out[6]= |
ReferenceAngle throws away the sign of its input:
| In[7]:= |
| Out[8]= |
This work is licensed under a Creative Commons Attribution 4.0 International License