Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RecursiveFunctionCallGraph (1.0.0) current version: 1.1.0 »

Source Notebook

Obtain a graph whose vertices and edges trace the evaluation of a recursive function

Contributed by: Bradley Klee and Thomas Adler

ResourceFunction["RecursiveFunctionCallGraph"][fun,inits,n]

returns the call graph for the nth value of recursive fun with initial conditions inits.

ResourceFunction["RecursiveFunctionCallGraph"][fun,inits,{n1,n2,…}]

allows multiple calls to fun, one for each of the inputs ni.

Details

A call graph is a directed acyclic graph whose vertices and edges are respectively a set of fun values and the immediate dependencies between them. The graph starts from one or more ni on its initial vertices, and follows another edge whenever it references another smaller value (by recursing). It terminates when it encounters a condition from inits.
The function fun must be specified as a rule: head[var]→form[var, head], where var and head are free symbols for the integer domain and range of a recursive function in some particular form.
The inits must also be specified as a rule or as a list of rules of the form: conditioni[var] → vali. When an integer value m is assigned to var, each conditioni[m] is checked by TrueQ. When one conditioni[m] evaluates to True, the function value is set as head[m]=vali.
The initial value vali can also be a function of var, i.e. conditioni[var] → vali[var], in which case a True conditioni[m] leads to the assignment head[m]=vali[m].
For example, fun=f[n]→f[n-1]+f[n-2] is the form of a typical linear recurrence with head=f, var=n, and form=Function[#2[#1-1]+#2[#1-2]]. The Fibonacci numbers have a special initial condition, inits={n<=1→n}, where condition=Function[#1<=1] with val=n. The initial condition can also be written as inits={n==0→0,n==1→1}, with two condition expressions and two val values.
Nested recursive functions are recursive functions where the right-hand-side of fun contains a term like head[…] that again contains one or more instances of head[…] somewhere in its argument pattern. For example, the Hofstadter G function is defined by fun=f[n]→n-f[f[n-1]] with inits={n==0→0}. ResourceFunction["RecursiveFunctionCallGraph"] supports such functions.
Linear recurrences such as Fibonacci are simple examples, whose call Graphs are typically the GraphUnion of a set of PathGraphs. Nested recursive functions lead to more complex graph structures such as trees with fractal or pseudorandom branching.
ResourceFunction["RecursiveFunctionCallGraph"] takes all options of Graph, and two more options related to computation and display: Method and "AddFigures".
Method can be set to either "Stack" or "SelfReferential". The default "Stack" method never experiences difficulties with $RecursionLimit. The "SelfReferential" method can typically compute the same data in shorter time, but might encounter TerminatedEvaluation from hitting $RecursionLimit.
When "AddFigures" is set to True, the vertices of the returned Graph are transformed into framed labels containing particular function values.
To avoid runaway iterations, it is generally assumed that evaluation of f[n] does not depend on any f[m] satisfying 0<n<m. If and when this condition becomes invalid, a Failure object is thrown. This safety feature is nice to have when exploring function spaces.

Examples

Basic Examples (2) 

A path Graph for a simple recursion producing consecutive integers:

In[1]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 10]
Out[1]=

The call Graph for the 10th Fibonacci number:

In[2]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, 10]
Out[2]=

Add vertex figures with function values:

In[3]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, 10, "AddFigures" -> True, GraphLayout -> "SpringElectricalEmbedding"]
Out[3]=

Scope (6) 

Add EdgeStyle by tag for the Fibonacci call graph:

In[4]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, 10, "AddFigures" -> True, GraphLayout -> "SpringElectricalEmbedding", EdgeStyle -> {x_ :> Directive[Switch[Last[x], 1, Blend[{Green, Red}, .75], 2, Blend[{Blue, Green}, .65] ], Thick]} ]
Out[4]=

The recurrence f[2n] = f[2n+1] = f[n]+1 has a perfect binary tree as its call graph when evaluated over a range from zero to one less than a power of two:

In[5]:=
Module[{shift, g1}, shift[x_Integer, b_Integer] := FromDigits[Most[IntegerDigits[x, b]], b]; g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][shift[\[FormalN], 2]], {\[FormalN] == 0 -> 1}, Range[15], "AddFigures" -> True, AspectRatio -> 2/3]]
Out[5]=

A nestedly-recursive function leading to hyperbolic Graph structure:

In[6]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 200]
Out[6]=

Extract function values from the VertexList:

In[7]:=
VertexList[ ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 50]][[All, 2]]
Out[7]=

Compare with OEIS A005206, "Hofstadter G-sequence":

In[8]:=
SameQ[%, ResourceFunction["OEISSequence"]["A005206"][[1 ;; 51]]]
Out[8]=

Select the outer call tree by deleting inner PathGraph edges:

In[9]:=
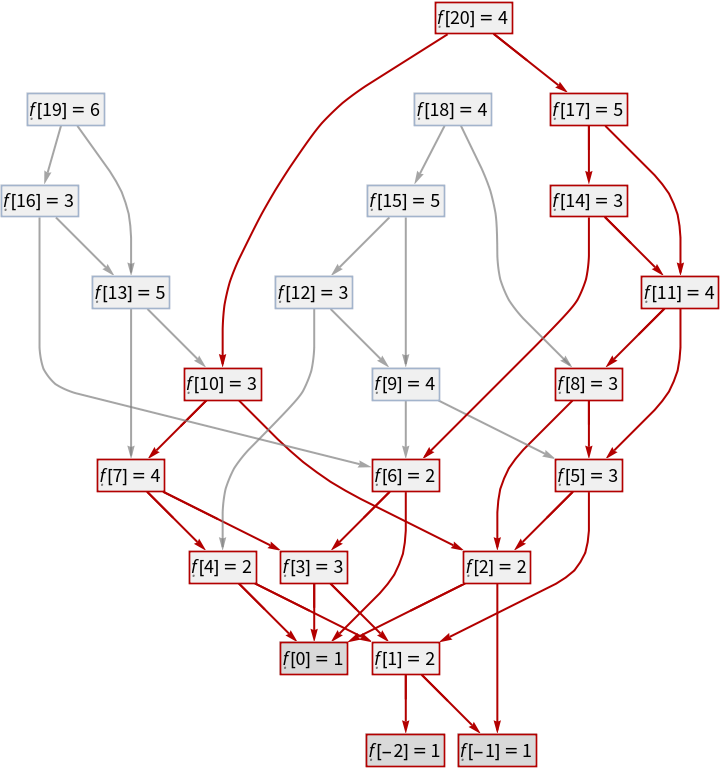
With[{g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 32, "AddFigures" -> True, GraphLayout -> "LayeredDigraphEmbedding"]}, EdgeDelete[g1, Cases[EdgeList[g1], _[_, _, 1]]]]
Out[9]=

Using a Range for the third argument can result in a call graph with more initial conditions:

In[10]:=
HighlightGraph[ ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, Range[20], "AddFigures" -> True], ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, 20]]
Out[10]=

Single-Rule initial conditions do not need to be wrapped in a List:

In[11]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], \[FormalN] <= 0 -> 1, Range[20]]
Out[11]=

Options (2) 

Setting "AddFigures" to true automatically insets the function values:

In[12]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 5, "AddFigures" -> True, GraphLayout -> "SpringElectricalEmbedding"]
Out[12]=

The "SelfReferential" Method is typically faster than the alternative, "Stack":

In[13]:=
AbsoluteTiming[ ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, Range[10000], Method -> #]][[1]] & /@ {"Stack", "SelfReferential"}
Out[13]=

Applications (1) 

Calculate the values of a special p-recurrence:

In[14]:=
VertexList[ ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1/(2 \[FormalN]^2)*((59 \[FormalN]^2 - 59 \[FormalN] + 20) \[FormalF][\[FormalN] - 1] - 12 (6 \[FormalN] - 7) (6 \[FormalN] - 5) \[FormalF][\[FormalN] - 2]), {\[FormalN] == 0 -> 1, \[FormalN] == 1 -> 10}, Range[10], VertexLabels -> {x_ :> x}]]
Out[14]=

Properties and Relations (2) 

Edges in the call Graph fall into subsets according to their tags:

In[15]:=
With[{g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, Range[20], "AddFigures" -> True]}, HighlightGraph[g1, MapThread[ Style[#1, Thick, #2] &, {Graph /@ Values[GroupBy[EdgeList[g1], Last]], {Red, Darker@Green}}]]]
Out[15]=

Tag-specific subgraphs have even finer subgraph structure according to which root node they reach:

In[16]:=
With[{g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, Range[20], "AddFigures" -> True]}, HighlightGraph[g1, MapThread[Function[{key, cols}, MapThread[Style[Subgraph[g1, #1], Thick, #2] &, { WeaklyConnectedComponents[ Graph[GroupBy[EdgeList[g1], Last][key]]], cols }]], {{1, 2}, {Blend[{Yellow, Red}, #/3] & /@ Range[3], {Blend[{Lighter@Blue, Darker@Green}], Blend[{Yellow, Darker@Green}]}}}]]]
Out[16]=

Plot function values according to subgraph membership:

In[17]:=
With[{g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, Range[100]]}, MapThread[Function[{key, col}, ListStepPlot[Map[Sort, ReplaceAll[WeaklyConnectedComponents[ Graph[GroupBy[EdgeList[g1], Last][key]]], \[FormalF][x_] == y_ :> {x, y}]], PlotStyle -> col, ImageSize -> 250, PlotRange -> {{-5, 100}, Automatic}, AxesOrigin -> {-5, 0}] ], {{1, 2}, {Blend[{Red, Yellow}, #/4] & /@ Range[3], {Blend[{Lighter@Blue, Darker@Green}], Blend[{Yellow, Darker@Green}]}}} ] ]
Out[17]=

Choice of Method should not affect the result, provided a TerminatedEvaluation is not encountered:

In[18]:=
Apply[SameQ, ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 100, Method -> #] & /@ {"Stack", "Referential"}]
Out[18]=

Possible Issues (2) 

Non-terminating recursions should result in a Failure object:

In[19]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] + 1], {\[FormalN] == 0 -> 0}, 2]
Out[19]=

The "SelfReferential" method sometimes exceeds $RecursionLimit:

In[20]:=
ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 1000, Method -> "SelfReferential"]
Out[20]=

The "Stack" method will not have this issue:

In[21]:=
VertexCount[ ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 1000, Method -> "Stack"]]
Out[21]=

Neat Examples (4) 

Turn the Hofstadter G function call Graph into a hyperbolic tiling:

In[22]:=
Module[{g1, ug1, threes, fours, vertices}, g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 400]; g1 = VertexDelete[g1, Alternatives @@ VertexList[g1][[{1, 2, 3, 4}]]]; ug1 = UndirectedGraph[g1]; threes = FindCycle[ug1, {3}, All]; fours = FindCycle[ug1, {4}, All]; vertices = Association[Thread[VertexList[g1] -> GraphEmbedding[g1]]]; Graphics[{ EdgeForm[Black], Blend[{Green, Red}, .75], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ threes, Blend[{Blue, Green}, .65], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ fours }] ]
Out[22]=

Trace a spiral from the center to the outer edge:

In[23]:=
Module[{g1, ug1, threes, fours, vertices, path, iteratePath, lastinds, now, next}, g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 400]; g1 = VertexDelete[g1, Alternatives @@ VertexList[g1][[{1, 2, 3, 4}]]]; ug1 = Graph[Sort@*UndirectedEdge @@@ EdgeList[g1][[All, 1 ;; 2]]]; threes = SortBy[FindCycle[ug1, {3}, All], Total[#[[All, 1, 1, 1]]] &]; fours = SortBy[FindCycle[ug1, {4}, All], Total[#[[All, 1, 1, 1]]] &]; vertices = Association[Thread[VertexList[g1] -> GraphEmbedding[g1]]]; iteratePath := Function[{threes, fours}, Function[path, lastinds = Map[FirstCase[ Reverse[path], #[ Pattern[x, Blank[]]] :> x]& , {\[FormalT], \[FormalS]}]; lastinds = lastinds + 1; now = Part[ Switch[ Part[ Last[path], 0], \[FormalT], threes, \[FormalS], fours], Part[ Last[path], 1]]; now = Join[now, Map[Reverse, now]]; next = Which[ And[Part[lastinds, 1] <= Length[threes], IntersectingQ[now, Part[threes, Part[lastinds, 1]]]], { \[FormalT][ Part[lastinds, 1]]}, And[Part[lastinds, 2] <= Length[fours], IntersectingQ[now, Part[fours, Part[lastinds, 2]]]], { \[FormalS][ Part[lastinds, 2]]}, True, {}]; Join[path, next]]]; path = {\[FormalS][1], \[FormalT][1], \[FormalS][2], \[FormalS][3]}; path = FixedPoint[iteratePath[threes, fours], path]; path = path /. { \[FormalS][x_] :> Mean[Lookup[vertices, fours[[x]][[All, 1]]]], \[FormalT][x_] :> Mean[Lookup[vertices, threes[[x]][[All, 1]]]]}; Graphics[{ EdgeForm[Lighter@Gray], Lighter[#, .7] &@Blend[{Green, Red}, .75], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ threes, Lighter[#, .7] &@Blend[{Blue, Green}, .65], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ fours, Thick, Blend[{Blue, Purple}, .4], Line[path] }] ]
Out[23]=

Obtain the binary sequence of squares and triangles along the spiral:

In[24]:=
Module[{g1, ug1, threes, fours, vertices, path, iteratePath, lastinds, now, next}, g1 = ResourceFunction["RecursiveFunctionCallGraph", ResourceVersion->"1.0.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 400]; g1 = VertexDelete[g1, Alternatives @@ VertexList[g1][[{1, 2, 3, 4}]]]; ug1 = Graph[Sort@*UndirectedEdge @@@ EdgeList[g1][[All, 1 ;; 2]]]; threes = SortBy[FindCycle[ug1, {3}, All], Total[#[[All, 1, 1, 1]]] &]; fours = SortBy[FindCycle[ug1, {4}, All], Total[#[[All, 1, 1, 1]]] &]; vertices = Association[Thread[VertexList[g1] -> GraphEmbedding[g1]]]; iteratePath := Function[{threes, fours}, Function[path, lastinds = Map[FirstCase[ Reverse[path], #[ Pattern[x, Blank[]]] :> x]& , {\[FormalT], \[FormalS]}]; lastinds = lastinds + 1; now = Part[ Switch[ Part[ Last[path], 0], \[FormalT], threes, \[FormalS], fours], Part[ Last[path], 1]]; now = Join[now, Map[Reverse, now]]; next = Which[ And[Part[lastinds, 1] <= Length[threes], IntersectingQ[now, Part[threes, Part[lastinds, 1]]]], { \[FormalT][ Part[lastinds, 1]]}, And[Part[lastinds, 2] <= Length[fours], IntersectingQ[now, Part[fours, Part[lastinds, 2]]]], { \[FormalS][ Part[lastinds, 2]]}, True, {}]; Join[path, next]]]; path = {\[FormalS][1], \[FormalT][1], \[FormalS][2], \[FormalS][3]}; path = FixedPoint[iteratePath[threes, fours], path]; path[[All, 0]] /. {\[FormalS] -> 0, \[FormalT] -> 1} ]
Out[24]=

Compare with OEIS A003849 "The infinite Fibonacci word":

In[25]:=
SameQ[%, Last[SubstitutionSystem[{0 -> {0, 1}, 1 -> {0}}, {0}, 15] ][[6 ;; -1]][[1 ;; Length[%]]]]
Out[25]=

Publisher

Brad Klee

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.1.0 – 18 September 2024
  • 1.0.0 – 16 September 2024

Related Resources

Author Notes

Thomas Adler wrote the first version of the "Stack" method at Summer School 2024. Bradley Klee edited the "Stack" method and integrated it with the "SelfReferential" method while working on a blog with Stephen Wolfram.

License Information