Details
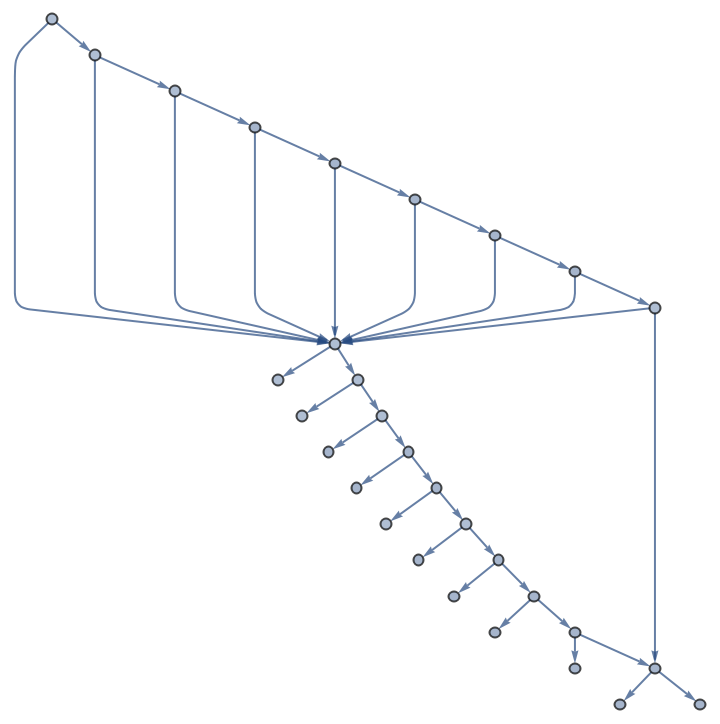
A call graph is a directed acyclic graph whose vertices and edges are respectively a set of fun values and the immediate dependencies between them. The graph starts from one or more ni on its initial vertices, and follows another edge whenever it references another smaller value (by recursing). It terminates when it encounters a condition from inits.
The function fun must be specified as a rule: head[var]→form[var, head], where var and head are free symbols for the integer domain and range of a recursive function in some particular form.
The
inits must also be specified as a rule or as a list of rules of the form:
conditioni[
var] →
vali. When an integer value
m is assigned to
var, each
conditioni[
m] is checked by
TrueQ. When one
conditioni[
m] evaluates to
True, the function value is set as
head[
m]=
vali.
The initial value
vali can also be a function of
var, i.e.
conditioni[
var] →
vali[
var], in which case a
True conditioni[
m] leads to the assignment
head[
m]=
vali[
m].
For example,
fun=f[n]→f[n-1]+f[n-2] is the form of a typical linear recurrence with
head=f,
var=n, and
form=Function[#2[#1-1]+#2[#1-2]]. The
Fibonacci numbers have a special initial condition,
inits={
n<=1→n}, where
condition=Function[#1<=1] with
val=n. The initial condition can also be written as
inits={n==0→0,n==1→1}, with two
condition expressions and two
val values.
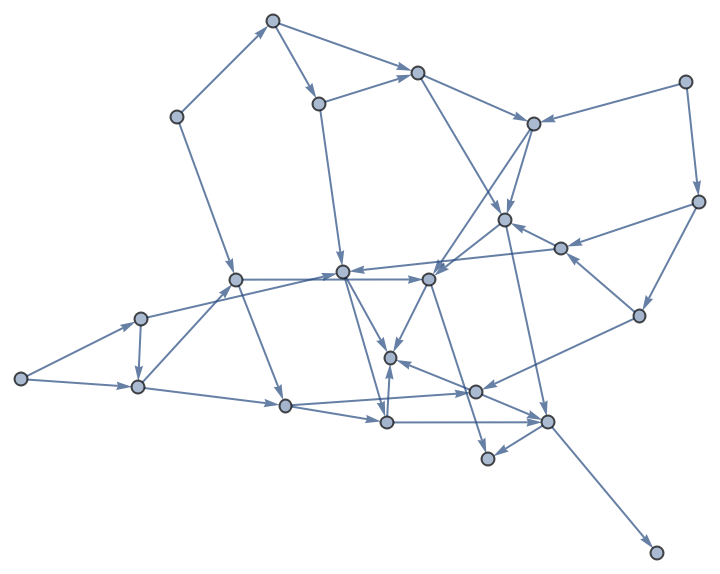
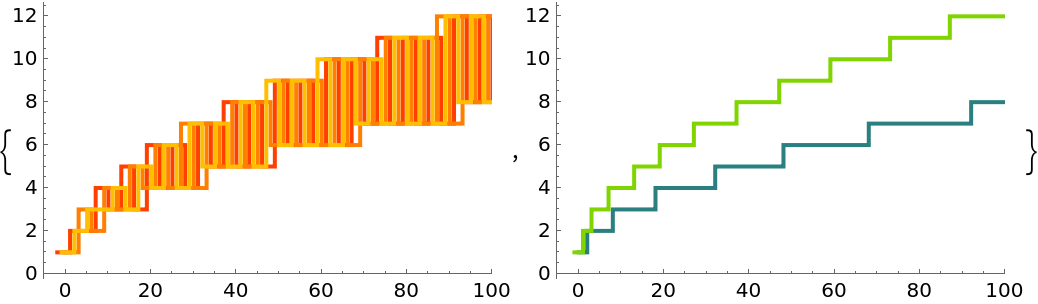
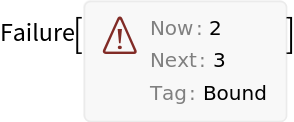
Nested recursive functions are recursive functions where the right-hand-side of fun contains a term like head[…] that again contains one or more instances of head[…] somewhere in its argument pattern. For example, the Hofstadter G function is defined by fun=f[n]→n-f[f[n-1]] with inits={n==0→0}. ResourceFunction["RecursiveFunctionCallGraph"] supports such functions.
Linear recurrences such as
Fibonacci are simple examples, whose call
Graphs are typically the
GraphUnion of a set of
PathGraphs. Nested recursive functions lead to more complex graph structures such as trees with fractal or pseudorandom branching.
ResourceFunction["RecursiveFunctionCallGraph"] takes all options of
Graph, and three more options related to computation and display:
Method,
"AddFigures", and "Bounding".
When
"AddFigures" is set to
True, the vertices of the returned
Graph are transformed into framed labels containing particular function values.
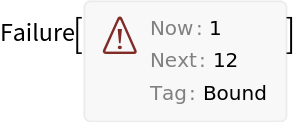
To avoid runaway iterations, it is generally assumed that evaluation of
f[n] does not depend on any
f[m] satisfying
0<n<m. If and when this condition becomes invalid, a
Failure object is thrown. This safety feature is nice to have when exploring function spaces. Setting option "Bounding" to
False, removes the safety guard to potentially enable more unusual results.
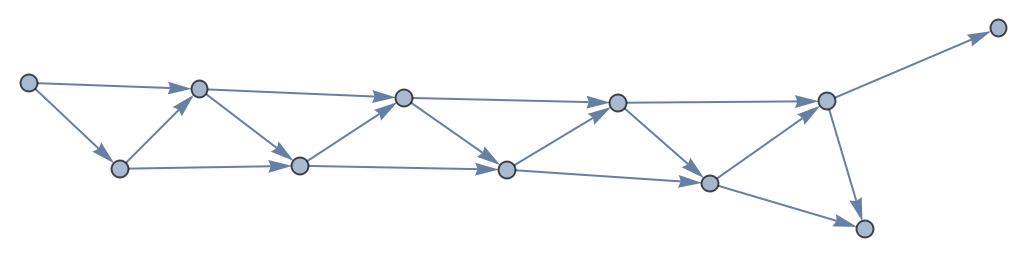

![ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, 10,
"AddFigures" -> True, GraphLayout -> "SpringElectricalEmbedding",
EdgeStyle -> {x_ :> Directive[Switch[Last[x],
1, Blend[{Green, Red}, .75], 2, Blend[{Blue, Green}, .65]
], Thick]}
]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/06d6fedef3df0069.png)
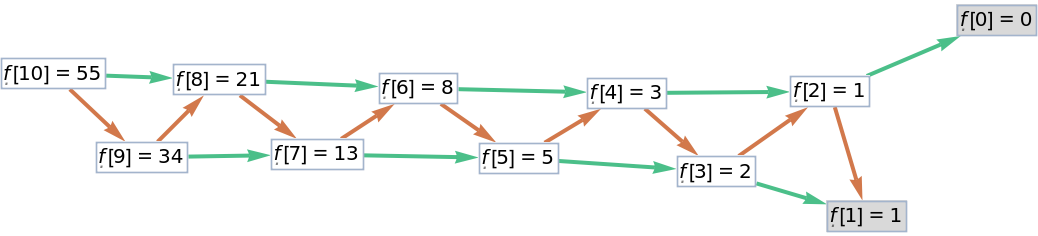
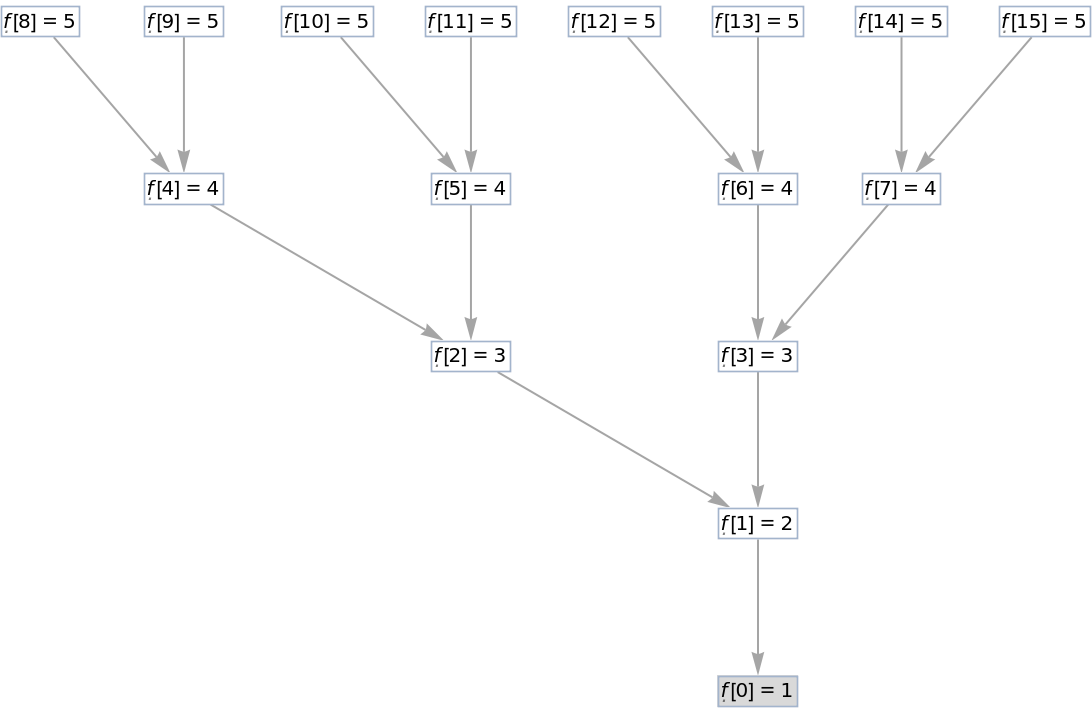
![VertexList[
ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]],
{\[FormalN] == 0 -> 0}, 50]][[All, 2]]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/70d9a33f8e170adc.png)
![With[{g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 32,
"AddFigures" -> True, GraphLayout -> "LayeredDigraphEmbedding"]},
EdgeDelete[g1, Cases[EdgeList[g1], _[_, _, 1]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/4a4d2b7760bf1e19.png)
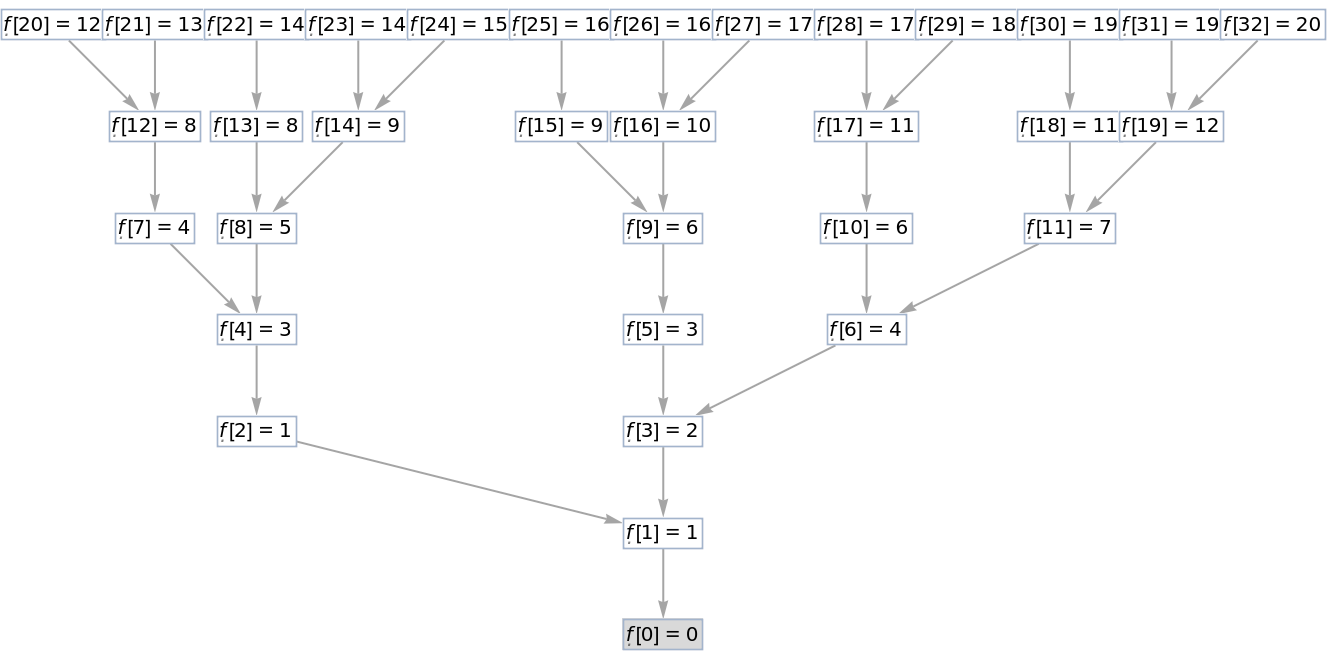
![HighlightGraph[
ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, Range[20],
"AddFigures" -> True], ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, 20]]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/6633485b1346dba7.png)

![AbsoluteTiming[
ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, Range[10000], Method -> #]][[1]] & /@ {"Stack", "SelfReferential"}](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/28f60e819516b8b1.png)
![With[{g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]], {\[FormalN] <= 0 -> 1}, Range[20], "AddFigures" -> True]},
HighlightGraph[g1, MapThread[
Style[#1, Thick, #2] &, {Graph /@ Values[GroupBy[EdgeList[g1], Last]],
{Red, Darker@Green}}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/23be6341e9565911.png)
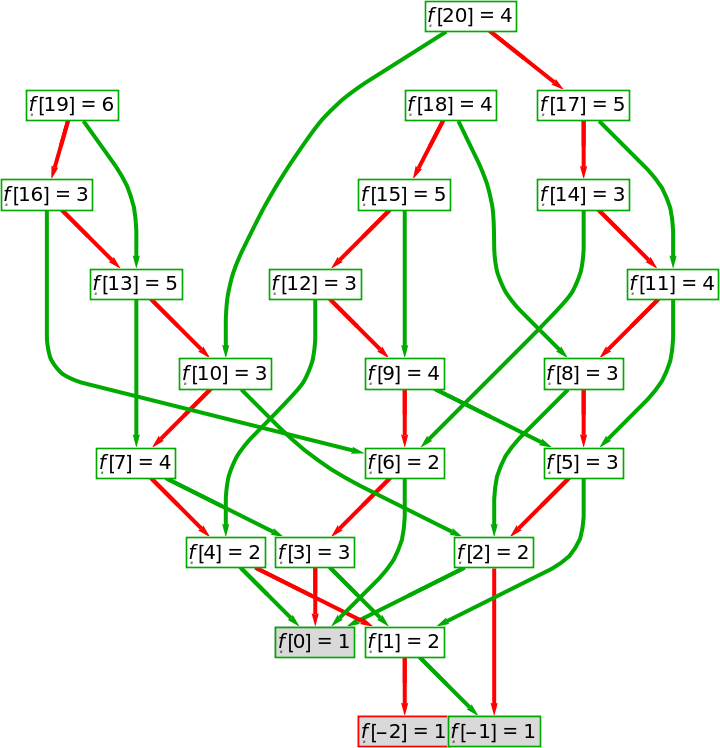
![With[{g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]],
{\[FormalN] <= 0 -> 1}, Range[20], "AddFigures" -> True]},
HighlightGraph[g1, MapThread[Function[{key, cols},
MapThread[Style[Subgraph[g1, #1], Thick, #2] &, {
WeaklyConnectedComponents[
Graph[GroupBy[EdgeList[g1], Last][key]]], cols
}]], {{1, 2}, {Blend[{Yellow, Red}, #/3] & /@ Range[3], {Blend[{Lighter@Blue, Darker@Green}],
Blend[{Yellow, Darker@Green}]}}}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/5f4ef30e63ae3bd5.png)
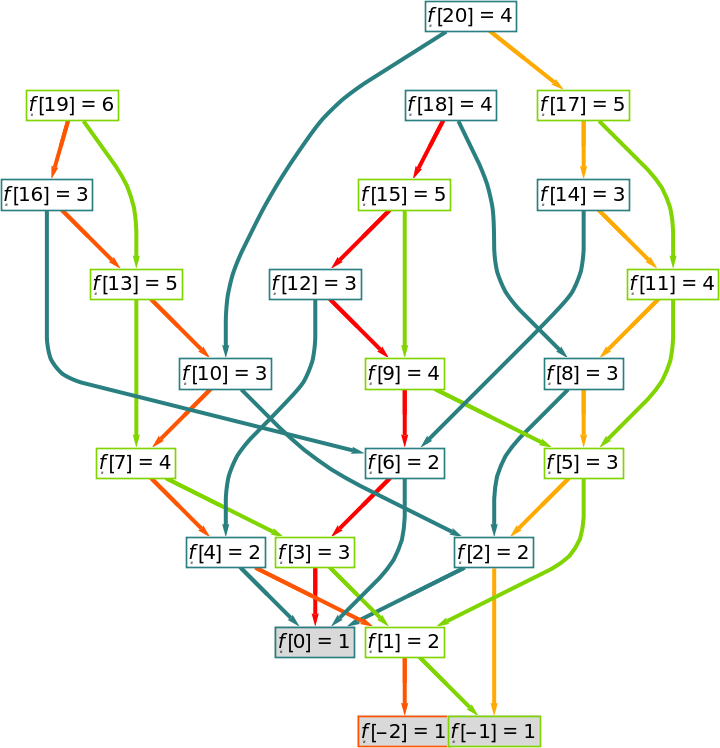
![With[{g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 2 \[FormalF][\[FormalN] - 3]],
{\[FormalN] <= 0 -> 1}, Range[100]]},
MapThread[Function[{key, col},
ListStepPlot[Map[Sort, ReplaceAll[WeaklyConnectedComponents[
Graph[GroupBy[EdgeList[g1], Last][key]]], \[FormalF][x_] == y_ :> {x, y}]],
PlotStyle -> col, ImageSize -> 250,
PlotRange -> {{-5, 100}, Automatic}, AxesOrigin -> {-5, 0}]
], {{1, 2}, {Blend[{Red, Yellow}, #/4] & /@ Range[3], {Blend[{Lighter@Blue, Darker@Green}],
Blend[{Yellow, Darker@Green}]}}} ]
]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/3f6a33bd03c7eabb.png)
![Apply[SameQ, ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1],
{\[FormalN] == 0 -> 0}, 100, Method -> #] & /@ {"Stack", "Referential"}]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/4946e5e45202c5a2.png)
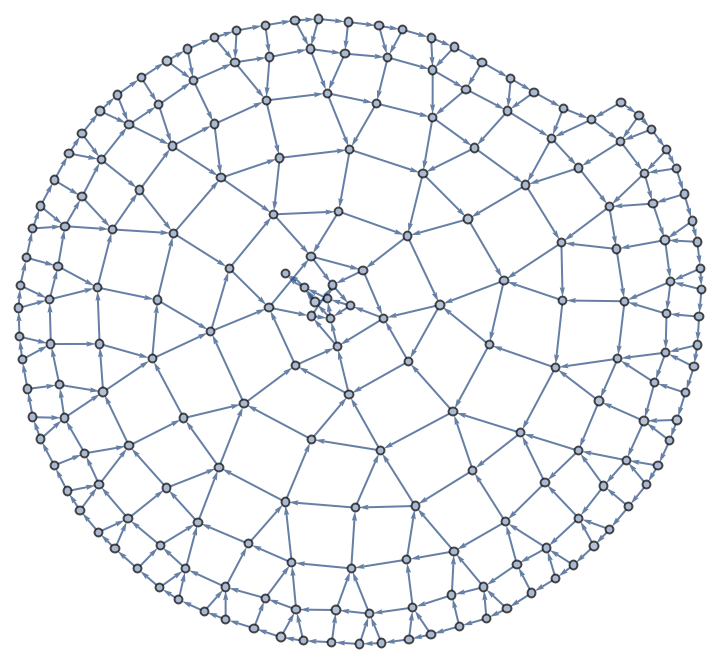
![Module[{g1, ug1, threes, fours, vertices},
g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 400];
g1 = VertexDelete[g1, Alternatives @@ VertexList[g1][[{1, 2, 3, 4}]]];
ug1 = UndirectedGraph[g1];
threes = FindCycle[ug1, {3}, All];
fours = FindCycle[ug1, {4}, All];
vertices = Association[Thread[VertexList[g1] -> GraphEmbedding[g1]]];
Graphics[{
EdgeForm[Black],
Blend[{Green, Red}, .75], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ threes,
Blend[{Blue, Green}, .65], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ fours
}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/6689c99ea35e1ad8.png)
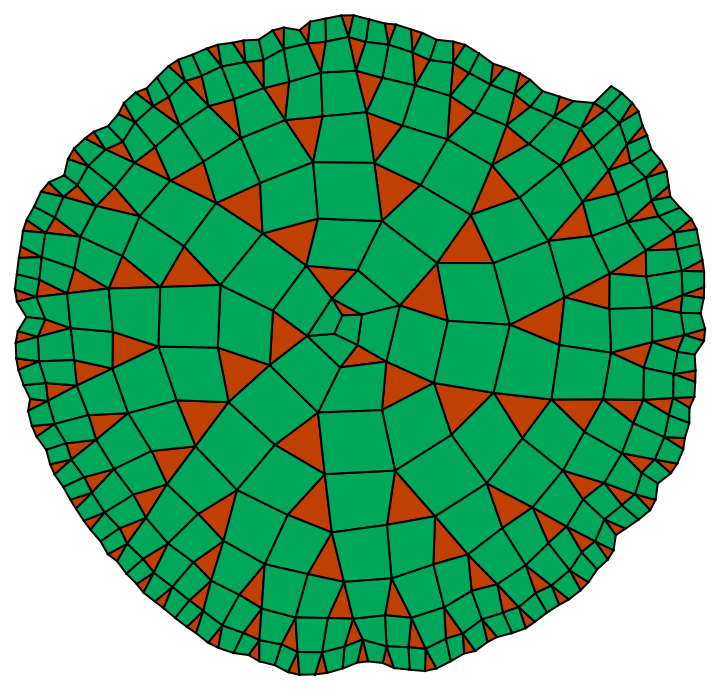
![Module[{g1, ug1, threes, fours, vertices, path, iteratePath,
lastinds, now, next},
g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 400];
g1 = VertexDelete[g1, Alternatives @@ VertexList[g1][[{1, 2, 3, 4}]]];
ug1 = Graph[Sort@*UndirectedEdge @@@ EdgeList[g1][[All, 1 ;; 2]]]; threes = SortBy[FindCycle[ug1, {3}, All], Total[#[[All, 1, 1, 1]]] &];
fours = SortBy[FindCycle[ug1, {4}, All], Total[#[[All, 1, 1, 1]]] &];
vertices = Association[Thread[VertexList[g1] -> GraphEmbedding[g1]]];
iteratePath := Function[{threes, fours},
Function[path, lastinds = Map[FirstCase[
Reverse[path], #[
Pattern[x,
Blank[]]] :> x]& , {\[FormalT], \[FormalS]}]; lastinds = lastinds + 1; now = Part[
Switch[
Part[
Last[path], 0], \[FormalT], threes, \[FormalS], fours],
Part[
Last[path], 1]]; now = Join[now,
Map[Reverse, now]]; next = Which[
And[Part[lastinds, 1] <= Length[threes],
IntersectingQ[now,
Part[threes,
Part[lastinds, 1]]]], {
\[FormalT][
Part[lastinds, 1]]},
And[Part[lastinds, 2] <= Length[fours],
IntersectingQ[now,
Part[fours,
Part[lastinds, 2]]]], {
\[FormalS][
Part[lastinds, 2]]}, True, {}]; Join[path, next]]];
path = {\[FormalS][1], \[FormalT][1], \[FormalS][2], \[FormalS][3]};
path = FixedPoint[iteratePath[threes, fours], path];
path = path /. {
\[FormalS][x_] :> Mean[Lookup[vertices, fours[[x]][[All, 1]]]],
\[FormalT][x_] :> Mean[Lookup[vertices, threes[[x]][[All, 1]]]]};
Graphics[{
EdgeForm[Lighter@Gray],
Lighter[#, .7] &@Blend[{Green, Red}, .75], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ threes,
Lighter[#, .7] &@Blend[{Blue, Green}, .65], Polygon[Lookup[vertices, #[[All, 1]]]] & /@ fours,
Thick, Blend[{Blue, Purple}, .4], Line[path] }] ]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/0b9f5201621982b1.png)
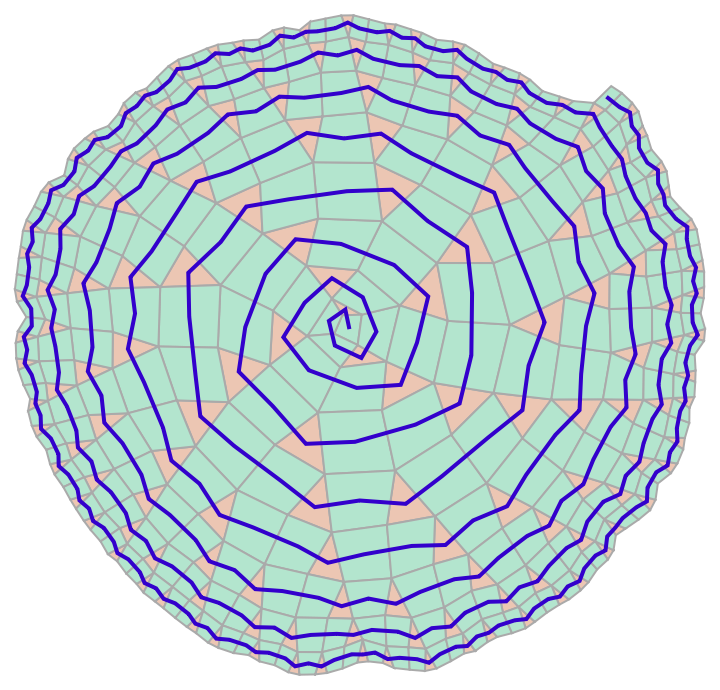
![Module[{g1, ug1, threes, fours, vertices, path, iteratePath,
lastinds, now, next},
g1 = ResourceFunction[
"RecursiveFunctionCallGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, 400];
g1 = VertexDelete[g1, Alternatives @@ VertexList[g1][[{1, 2, 3, 4}]]];
ug1 = Graph[Sort@*UndirectedEdge @@@ EdgeList[g1][[All, 1 ;; 2]]]; threes = SortBy[FindCycle[ug1, {3}, All], Total[#[[All, 1, 1, 1]]] &];
fours = SortBy[FindCycle[ug1, {4}, All], Total[#[[All, 1, 1, 1]]] &];
vertices = Association[Thread[VertexList[g1] -> GraphEmbedding[g1]]];
iteratePath := Function[{threes, fours},
Function[path, lastinds = Map[FirstCase[
Reverse[path], #[
Pattern[x,
Blank[]]] :> x]& , {\[FormalT], \[FormalS]}]; lastinds = lastinds + 1; now = Part[
Switch[
Part[
Last[path], 0], \[FormalT], threes, \[FormalS], fours],
Part[
Last[path], 1]]; now = Join[now,
Map[Reverse, now]]; next = Which[
And[Part[lastinds, 1] <= Length[threes],
IntersectingQ[now,
Part[threes,
Part[lastinds, 1]]]], {
\[FormalT][
Part[lastinds, 1]]},
And[Part[lastinds, 2] <= Length[fours],
IntersectingQ[now,
Part[fours,
Part[lastinds, 2]]]], {
\[FormalS][
Part[lastinds, 2]]}, True, {}]; Join[path, next]]];
path = {\[FormalS][1], \[FormalT][1], \[FormalS][2], \[FormalS][3]};
path = FixedPoint[iteratePath[threes, fours], path];
path[[All, 0]] /. {\[FormalS] -> 0, \[FormalT] -> 1}
]](https://www.wolframcloud.com/obj/resourcesystem/images/e45/e456c1ec-141e-4069-8169-cd72936b606f/1249155d574dd566.png)
