Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RecurrencePlot

Source Notebook

Visualize the recurrence of a single discrete time series on a lattice

Contributed by: Daniel de Souza Carvalho

ResourceFunction["RecurrencePlot"][ts]

shows the recurrence plot of the time series ts.

ResourceFunction["RecurrencePlot"][{ts1,ts2}]

shows the recurrence plot for a pair of time series.

Details and Options

A recurrence plot is a matrix visualization where columns and rows correspond to a certain pair of times on a lattice, and plot values are based on the difference of the times series values.
ResourceFunction["RecurrencePlot"] plots i for horizontal and j for vertical axes.
The recurrence plot is based on the function where is a unit step, ε is a threshold, where is a norm, and are each elements of the time series vectors.
ResourceFunction["RecurrencePlot"] has the same options as ArrayPlot, with the following additions:
"RecurrenceThreshold"1value of threshold ε used
"RecurrenceType""Standard"type of recurrence
With "RecurrenceType"→"Standard", is taken to be the UnitStep function.
With "RecurrenceType"→"Global", is taken to be the Identity function.

Examples

Basic Examples (1) 

Recurrence plot of list of random integers:

In[1]:=
ResourceFunction["RecurrencePlot"][RandomInteger[10, 30]]
Out[1]=

Scope (7) 

Recurrence plot of a one-dimensional list of ordered integers:

In[2]:=
ResourceFunction["RecurrencePlot"][Range[10, 30], Frame -> None, ColorFunction -> "Rainbow"]
Out[2]=

Recurrence plot of discrete data from a sine function:

In[3]:=
ResourceFunction["RecurrencePlot"][Table[Sin[x], {x, 0, 10, .1}]]
Out[3]=

Recurrence plot of a trigonometric operation:

In[4]:=
ResourceFunction["RecurrencePlot"][ Table[Sin[x]*Cos[y], {x, -10, 10, 1}, {y, -10, 10, 1}]]
Out[4]=

Recurrence plot of random and range discrete lists:

In[5]:=
ResourceFunction[ "RecurrencePlot"][{RandomInteger[10, 100], Range[100]}, "RecurrenceType" -> "Global" , ColorFunction -> GrayLevel, Frame -> None]
Out[5]=

Cross-recurrence plot from two random discrete lists:

In[6]:=
ResourceFunction[ "RecurrencePlot"][{RandomInteger[10, 100], RandomInteger[10, 100]}, ColorRules -> {0 -> Yellow, 1 -> Orange}, Frame -> None]
Out[6]=

Cross-recurrence plot of two trigonometric functions:

In[7]:=
ResourceFunction[ "RecurrencePlot"][{Table[Sin[x], {x, 0, 100, .5}], Table[Tan[x], {x, 0, 100, .5}]}]
Out[7]=

Global cross-recurrence plot of two random lists:

In[8]:=
ResourceFunction[ "RecurrencePlot"][{RandomInteger[10, 100], RandomInteger[10, 100]}, "RecurrenceType" -> "Global", ColorFunction -> Hue, Frame -> None]
Out[8]=

Options (1) 

All options from ArrayPlot can be used:

In[9]:=
ResourceFunction["RecurrencePlot"][RandomInteger[7, 100], Frame -> None]
Out[9]=

Applications (2) 

Global recurrence plot of elementary cellular automata rules:

In[10]:=
Manipulate[ ca = CellularAutomaton[rule, RandomInteger[1, 100], 100]; GraphicsGrid[{{ArrayPlot[ca, Frame -> None], ResourceFunction["RecurrencePlot"][Total[Transpose[ca]], "RecurrenceType" -> "Global", ColorFunction -> Hue, Frame -> None]}}], {{rule, 110}, 0, 255, 1}, SaveDefinitions -> True]
Out[10]=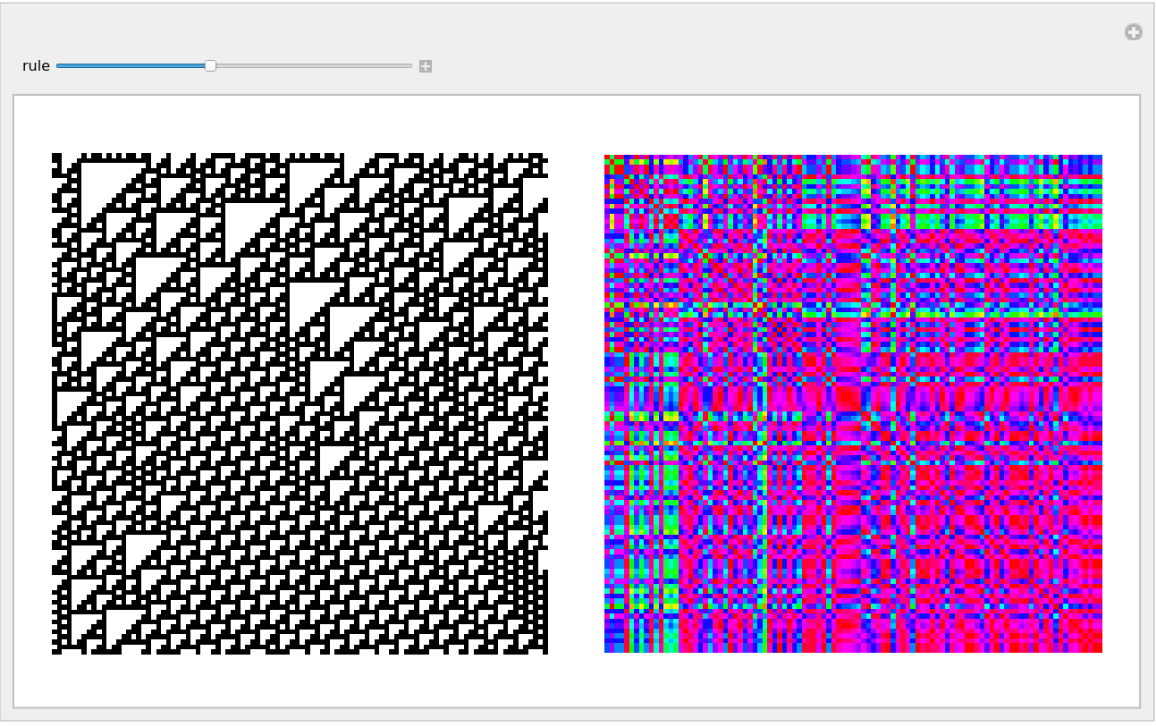

Visualize Bitcoin data:

In[11]:=
Take[Flatten[ ToCharacterCode[ BlockchainBlockData[300000, "TransactionList", BlockchainBase -> "Bitcoin"]]] - 60, 100]
Out[11]=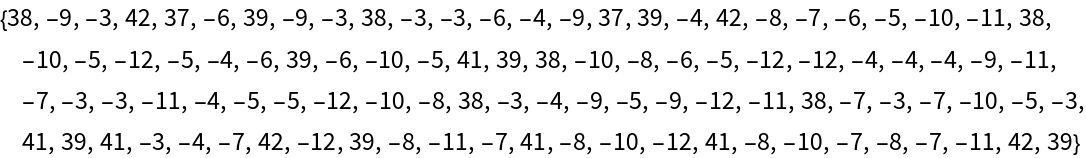
In[12]:=
ResourceFunction["RecurrencePlot"][%]
Out[12]=

Neat Examples (1) 

Dynamic visualization of a cross-recurrence plot of trigonometric functions:

In[13]:=
Manipulate[ResourceFunction["RecurrencePlot"][ {Table[Sin[x fx], {x, -10, 10, 1}], Table[Cos[y fy], {y, -10, 10, 1}]}], {{fx, 6}, 1, 10}, {{fy, 5}, 1, 10}, SaveDefinitions -> True]
Out[13]=

Publisher

Daniel de Souza Carvalho

Requirements

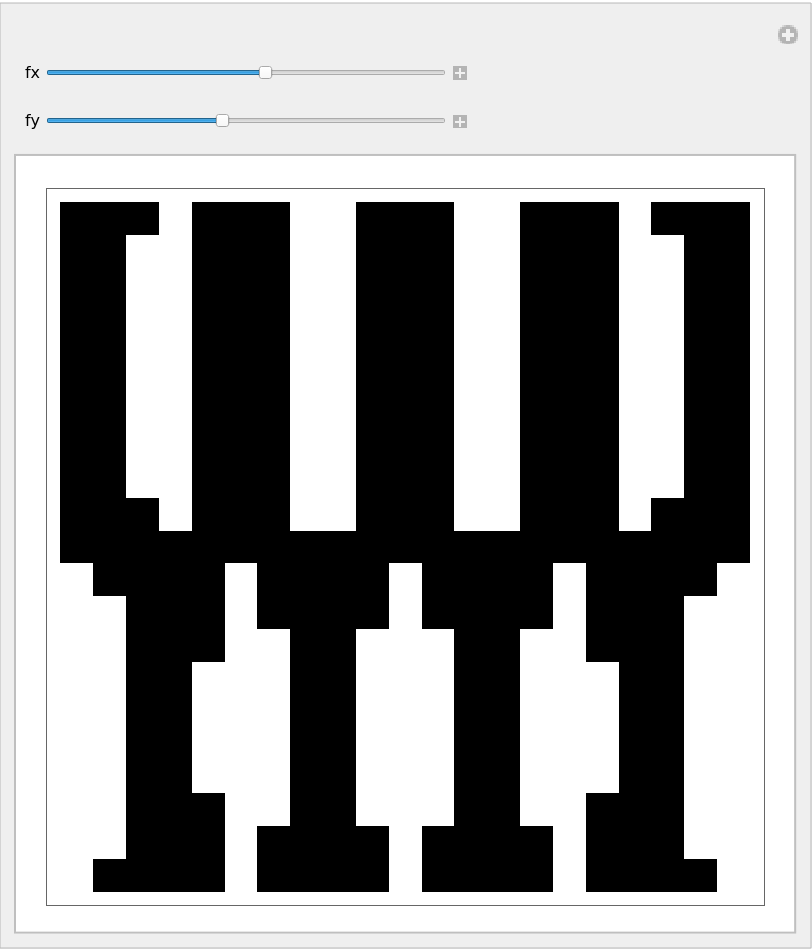Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 08 July 2024

Source Metadata

  • Citation:
    • N. Marwan, M. C. Romano, M. Thiel, J. Kurths, "Recurrence Plots for the Analysis of Complex Systems", Physics Reports, 438(5-6), 237-32, 2006.
      DOI: 10.1016/j.physrep.2006.11.001

Related Resources

Author Notes

More about the mathematical notations used here can be seen at: http://www.recurrence-plot.tk https://en.wikipedia.org/wiki/Recurrence_plot

License Information