Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Equivalent to Reap, but returns an association with tags as keys
ResourceFunction["ReapAssociation"][expr,patt] reaps only expressions sown with tags that match patt. | |
ResourceFunction["ReapAssociation"][expr,{patt1,patt2,…}] puts expressions associated with each of the patti in a separate list. | |
ResourceFunction["ReapAssociation"][expr,patt,f] has values f[tagi(ei,1,ei,2,...}] for each key tagi. |
Evaluate a sequence of expressions, "reaping" ones that have been "sown":
| In[1]:= |
| Out[1]= |
Compute a sum, "reaping" i^2 "sown" at each step:
| In[2]:= |
| Out[2]= |
Make a separate key for each tag being reaped:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |  |
If nothing is sown, an empty association will be returned in the "Sown" key:
| In[6]:= |
| Out[6]= |
Count the number of instances of each integer, separating the negative:
| In[7]:= |
| Out[7]= |
Apply f to each distinct key and list of values:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Find the list of values sampled by Plot:
| In[10]:= |
| Out[10]= | 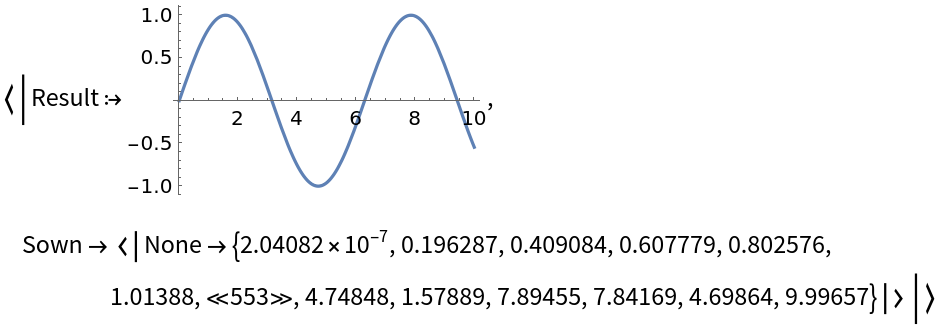 |
Remove duplicates from a list, keeping the original order:
| In[11]:= |
| In[12]:= |
| Out[12]= |
This is like Union without the sorting:
| In[13]:= |
| Out[13]= |
If no expressions are sown, ReapAssociation returns an empty association of expressions it has reaped:
| In[14]:= |
| Out[14]= |
ReapAssociation collects expressions in exactly the order they are sown:
| In[15]:= |
| Out[15]= |
The list associated with the first tag to be encountered will be the first key:
| In[16]:= |
| Out[16]= |
When the order of tags is not known, ReapAssociation can make it easier to understand results compared to Reap:
| In[17]:= |
| Out[7]= |
| In[18]:= |
| Out[10]= |
Create an animation showing the full stack history of an evaluation:
| In[19]:= | ![fib[0] := 1;
fib[1] := 1;
fib[n_] := fib[n - 2] + fib[n - 1];](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e5881e-0108-4ef1-90cf-93dd4d728d83/3e865d5d4113d0f2.png) |
| In[20]:= | ![ListAnimate[
DeleteDuplicates[
ResourceFunction["ReapAssociation"][
StackBegin[
TraceScan[StackInhibit[Sow[Column[Rest[Stack[_]]], "fib"]] &, Table[fib[i], {i, 5}]]]][["Sown", "fib"]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/08e/08e5881e-0108-4ef1-90cf-93dd4d728d83/7d5d18d83ab69b6d.png) |
| Out[20]= | 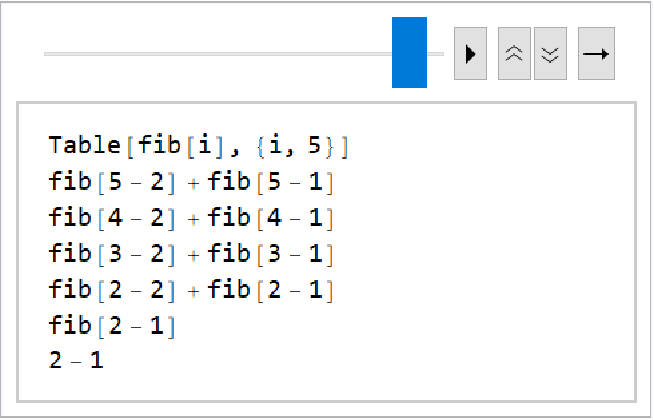 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License