Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RationalSmoothStep

Source Notebook

A sigmoidal interpolating rational function

Contributed by: Jan Mangaldan

ResourceFunction["RationalSmoothStep"][x]

gives a rational sigmoidal function between [0,1] for a position x in [0,1].

ResourceFunction["RationalSmoothStep"][n,x]

is the rational smoothstep function of order n at position x.

Details

The rational smoothstep function is defined as Rn(x)=xn/(xn+(1-x)n).
The rational smoothstep function can be used as a replacement for the usual polynomial-based smoothstep in computer graphics.
For x values less than 0 or greater than 1, the result clamps to 0 and 1, respectively.
ResourceFunction["RationalSmoothStep"][x] is equivalent to ResourceFunction["RationalSmoothStep"][3,x].
ResourceFunction["RationalSmoothStep"] can be evaluated to arbitrary numerical precision.
ResourceFunction["RationalSmoothStep"] automatically threads over lists.

Examples

Basic Examples (2) 

Interpolate at a position on a step:

In[1]:=
ResourceFunction["RationalSmoothStep"][2/3]
Out[1]=

Show rational smooth steps for multiple orders:

In[2]:=
Plot[Evaluate[ Table[ResourceFunction["RationalSmoothStep"][n, x], {n, 2, 4}]], {x, -1/2, 3/2}, PlotLegends -> Range[2, 4]]
Out[2]=

Scope (3) 

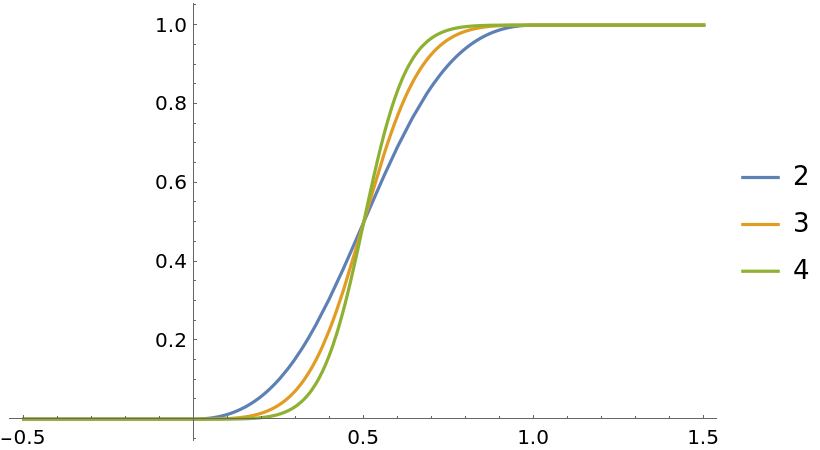Evaluate at an exact position:

In[3]:=
ResourceFunction["RationalSmoothStep"][4, 1/3]
Out[3]=

At a numeric position:

In[4]:=
ResourceFunction["RationalSmoothStep"][4, 0.33]
Out[4]=

RationalSmoothStep threads over lists:

In[5]:=
ResourceFunction["RationalSmoothStep"][Range[0, 3], 2/3]
Out[5]=
In[6]:=
ResourceFunction["RationalSmoothStep"][2, Subdivide[6]]
Out[6]=

Applications (1) 

Use RationalSmoothStep to implement a "smooth" version of Hue (reference):

In[7]:=
SmoothHue[n_Integer?NonNegative, h_?NumberQ, s_ : 1, b_ : 1] /; 0 <= s <= 1 && 0 <= b <= 1 := RGBColor[ b (1 - s + s ResourceFunction["RationalSmoothStep"][n, Clip[Abs[Mod[6 h + {0, 4, 2}, 6] - 3] - 1, {0, 1}]])]
In[8]:=
SmoothHue[1, 1/2, 2/3, 3/4]
Out[8]=
In[9]:=
Manipulate[ LinearGradientImage[ SmoothHue[n, #] &, {300, 30}], {{n, 2, "interpolation order"}, Range[5]}, SaveDefinitions -> True]
Out[9]=

Properties and Relations (1) 

RationalSmoothStep satisfies a symmetry relation:

In[10]:=
ResourceFunction["RationalSmoothStep"][-n, x] == ResourceFunction["RationalSmoothStep"][n, 1 - x] /. {n -> RandomInteger[{1, 5}], x -> RandomReal[]}
Out[10]=

Neat Examples (1) 

Use RationalSmoothStep to demonstrate "ease-in/ease-out":

In[11]:=
Manipulate[ Graphics[ Text["Zoom!", {ResourceFunction["RationalSmoothStep"][n, x], 0}], PlotRange -> {{-.1, 1.1}, {-.1, .1}}], {{n, 2}, 1, 5, 1}, {x, -1, 2, ControlType -> Animator, AnimationRunning -> False}]
Out[11]=

Version History

  • 1.0.1 – 15 March 2021
  • 1.0.0 – 10 March 2021

Related Resources

License Information