Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Partition a list into sublists with lengths proportional to weights in another list
ResourceFunction["RatioPartition"][list,{weight1,weight2, …}] splits list into sublists with lengths proportional to weight1,weight2, …. |
Partition a list into sublists containing 10%, 30% and 60% of the data:
| In[1]:= |
| Out[1]= |
Verify that there are no overlapping sublists:
| In[2]:= |
| Out[2]= |
Partition a list into sublists containing 22%, 27% and 51% of the data. This time, the partitions can only be approximated:
| In[3]:= |
| Out[3]= |
Partition a list into any number of parts:
| In[4]:= | ![Manipulate[
Grid[{{"n", "Sublists"}, Sequence @@ Thread[{Range[n], ResourceFunction["RatioPartition"][Range[20], RandomInteger[{1, Round[20/n]}, n]]}]}, Alignment -> {{Right, Left}}, BaseStyle -> "Text", Dividers -> {{2 -> LightGray}, {2 -> LightGray}}], {n, 1, 20, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/c5e/c5e7c58c-9a7f-4b70-905f-211702c5758d/5d1a906e96e3bf87.png) |
| Out[4]= | 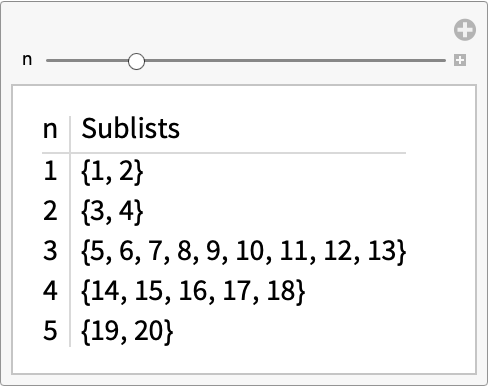 |
Partition a list using decimals or fractions:
| In[5]:= |
| Out[5]= |
Partition a list using weights that don’t sum to a power of 10:
| In[6]:= |
| Out[6]= |
Randomize the data before partitioning with the "Randomize" option:
| In[7]:= |
| Out[7]= |
RatioPartition is useful for separating data for training neural nets. Partition some randomized data into 60% training data, 20% validation data and 20% testing data:
| In[8]:= | ![{trainingData, validationData, testingData} = ResourceFunction["RatioPartition"][
ResourceData["MNIST", "TrainingData"], {60, 20, 20}, "Randomize" -> True];](https://www.wolframcloud.com/obj/resourcesystem/images/c5e/c5e7c58c-9a7f-4b70-905f-211702c5758d/2ba5820d7fa3259d.png) |
Train a classifier:
| In[9]:= |
| Out[9]= |  |
Measure the accuracy of the classifier:
| In[10]:= |
| Out[10]= |
When exact partitions are not possible, the order of the weights may affect the lengths of the resulting sublists:
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
The list of weights is scaled to the interval [0, 1]. Therefore, for best results, choose weights that add up to a power of 10. Not doing so may result in sublists of unexpected lengths:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Using a single weight will leave the list unchanged (albeit as a sublist):
| In[15]:= |
| Out[15]= |
Due to rounding, it is possible to have empty lists in the output:
| In[16]:= |
| Out[16]= |
Weights must be positive real numbers:
| In[17]:= |
| Out[17]= |
This work is licensed under a Creative Commons Attribution 4.0 International License