Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate random vectors in any dimension of unit length
ResourceFunction["RandomUnitVector"][d] generates a d-dimensional unit vector. | |
ResourceFunction["RandomUnitVector"][d,n] generates n d-dimensional unit vectors. | |
ResourceFunction["RandomUnitVector"][d,{n1,n2,n3,…}] generates an n1⨯n2⨯n3… array of d-dimensional unit vectors. |
Generate a two-dimensional unit vector:
| In[1]:= |
| Out[1]= |
Generate 5 random three-dimensional unit vectors:
| In[2]:= |
| Out[2]= |
Generate a 4×6 array of 3D unit vectors:
| In[3]:= |
| Out[3]= |  |
Check the dimensions:
| In[4]:= |
| Out[4]= |
Check the magnitudes:
| In[5]:= |
| Out[5]= |
Generate a random points on a circle:
| In[6]:= |
| Out[6]= |  |
Generate some random points on a sphere and compare with built-in functionality:
| In[7]:= | ![{
Graphics3D[ResourceFunction["RandomUnitVector"][3, 1000] // Point, ImageSize -> 200],
Graphics3D[RandomPoint[Sphere[], 1000] // Point, ImageSize -> 200]
}](https://www.wolframcloud.com/obj/resourcesystem/images/f5e/f5ed378a-da7e-47bf-aa0c-874829f64811/2e5732eb3441692e.png) |
| Out[7]= | 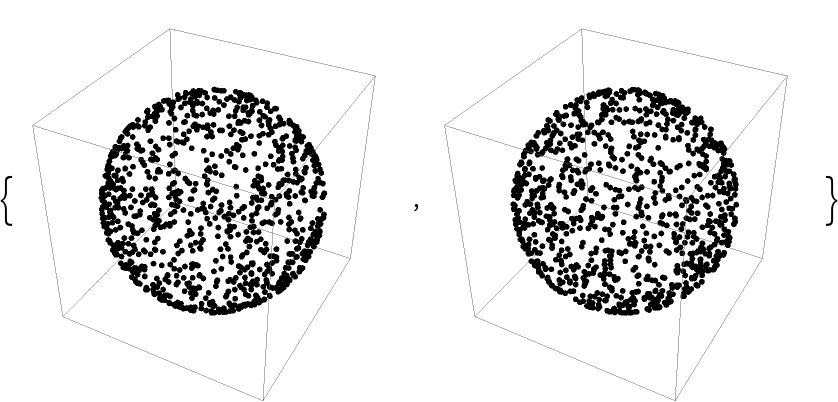 |
Check the uniformity of the unit vectors:
| In[8]:= |
| Out[8]= | 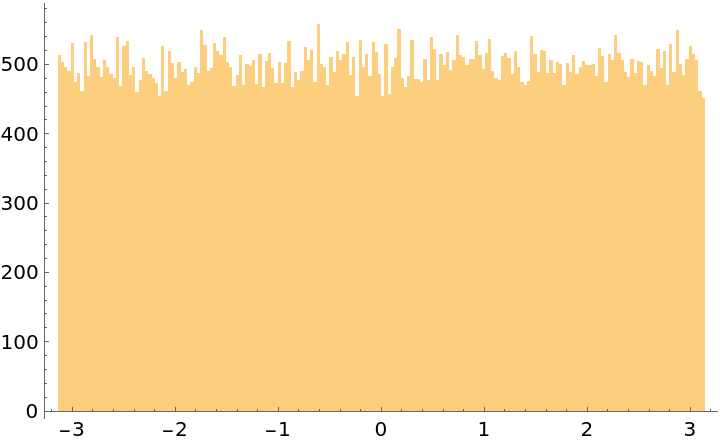 |
Perform a 2D random walk with steps of unit length:
| In[9]:= |
| Out[9]= |  |
Perform a 3D random walk with steps of unit length:
| In[10]:= |
| Out[10]= | 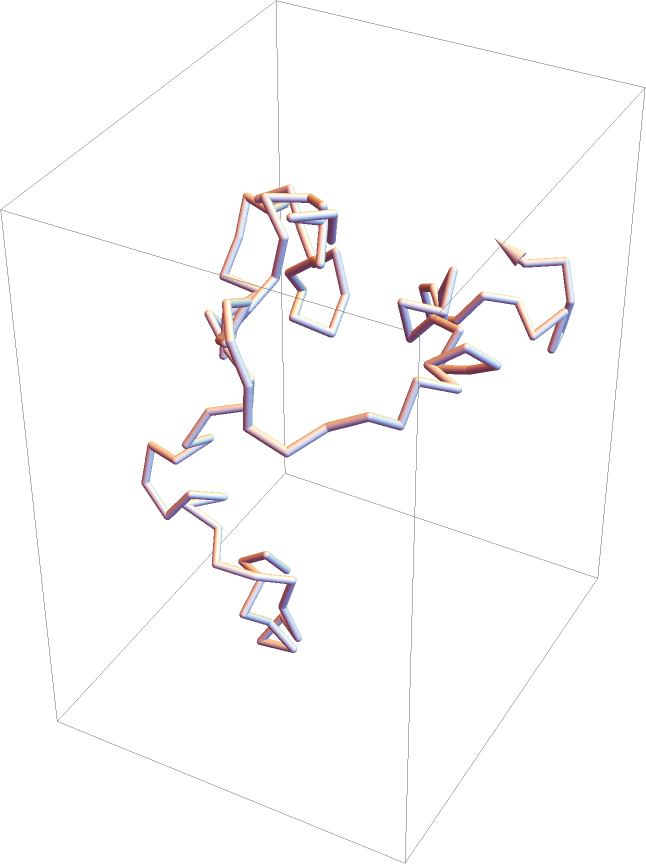 |
This work is licensed under a Creative Commons Attribution 4.0 International License