Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a maze based on the Sierpinski carpet
ResourceFunction["RandomSierpinskiMaze"][scale] returns the ArrayPlot of a maze drawn by connecting dots on a square fragment of the Sierpiński carpet fractal, whose length dimension roughly equals 3scale+1. | |
ResourceFunction["RandomSierpinskiMaze"][scale, AdjacencyGraph] returns a primitive Graph of the maze, which determines allowable moves on the corresponding ArrayPlot. |
Depict a basic unit of the randomized maze:
| In[1]:= |
| Out[2]= |  |
Scale up the basic unit by areal factors of 9:
| In[3]:= | ![With[{mazes = (SeedRandom["Basic"];
ResourceFunction["RandomSierpinskiMaze"][#, PixelConstrained -> 4] & /@ Range[0, 3])},
Grid[Partition[mazes, 2],
Alignment -> Center, Spacings -> {2, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/75f1852fb88657b0.png) |
| Out[3]= |  |
Compare the ArrayPlot with its primitive Graph:
| In[4]:= | ![With[{graph0 = (SeedRandom["Compare"];
ResourceFunction["RandomSierpinskiMaze"][2, AdjacencyGraph])},
Row[{Graph[#, VertexCoordinates -> (# -> # & /@ VertexList[#]),
ImageSize -> 29 6
] &@graph0,
Style["\[LongRightArrow]", 32, Bold, Gray],
SeedRandom["Compare"];
ResourceFunction["RandomSierpinskiMaze"][2, PixelConstrained -> 6]},
Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/22e56eb9949103d3.png) |
| Out[4]= |  |
Display the same Graph coordinate-free and highlight a shortest path between corners:
| In[5]:= | ![With[{graph0 = (SeedRandom["Compare"];
ResourceFunction["RandomSierpinskiMaze"][2, AdjacencyGraph])},
HighlightGraph[graph0, PathGraph[
FindShortestPath[graph0, {1, 29}, {29, 1}]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/6e8f05b86e432f8a.png) |
| Out[5]= | 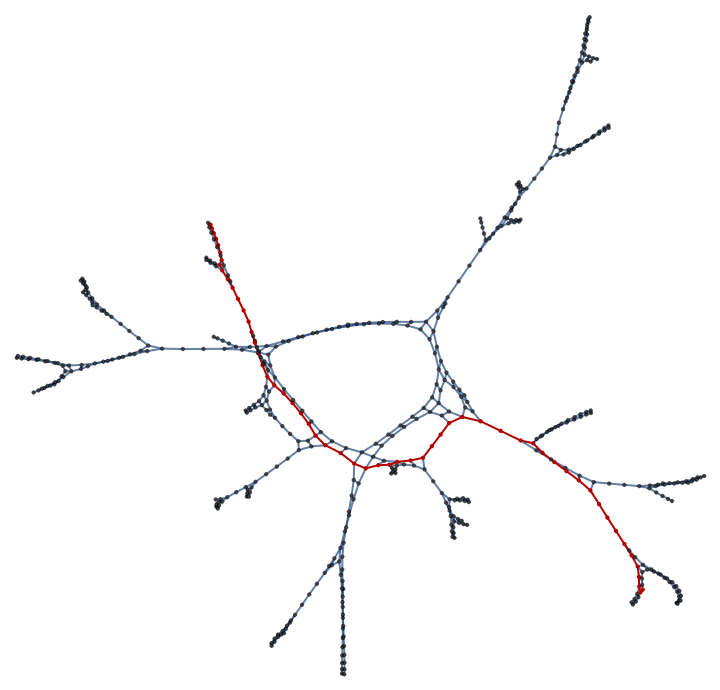 |
Depict the path in an ArrayPlot:
| In[6]:= | ![With[{path0 = FindShortestPath[
SeedRandom["Compare"];
ResourceFunction["RandomSierpinskiMaze"][2, AdjacencyGraph],
{1, 29}, {29, 1}]},
ArrayPlot[ReplacePart[
SeedRandom["Compare"];
Reverse[ResourceFunction["RandomSierpinskiMaze"][2][[1, 1]]],
Reverse[# {1, -1} + {1, -1}] -> 1 & /@ path0],
Frame -> None, ColorRules -> {4 -> LightGray,
5 -> White, 0 -> Black, 1 -> Lighter[Red, 0.5]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/6ccda817d8623910.png) |
| Out[6]= | 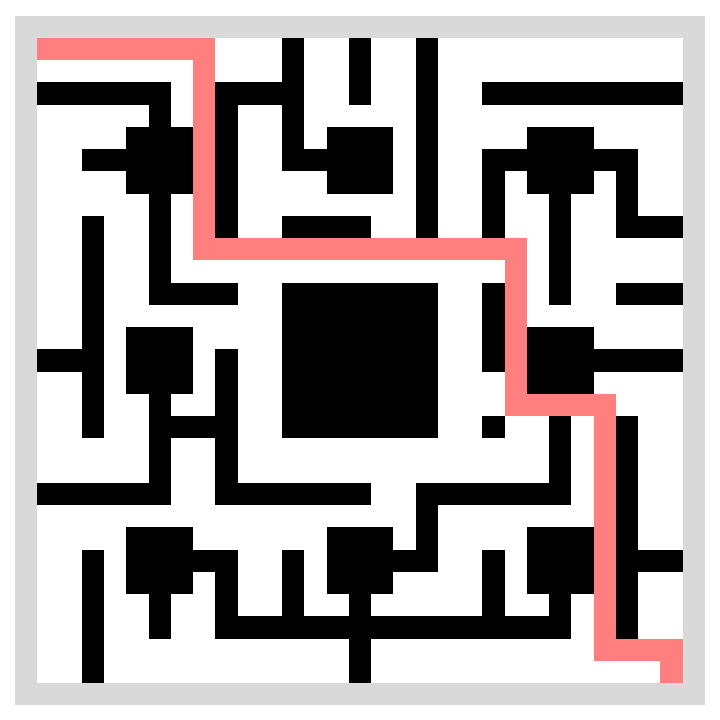 |
The measured complexity is super-exponential with regard to input scale, but it is possible to obtain mazes up to scale=4 in reasonable time:
| In[7]:= | ![With[{data = AbsoluteTiming[
ResourceFunction["RandomSierpinskiMaze"][#];][[1]] & /@ Range[3]},
Show[LogPlot[Evaluate[
A Exp[ Exp[k x]] /. FindFit[data,
A Exp[Exp[k x]], {A, k}, x]], {x, 0, 4},
AxesLabel -> {"scale", "time(s)"}],
ListLogPlot[data, PlotStyle -> Red]]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/35756fb41b45474e.png) |
| Out[7]= | 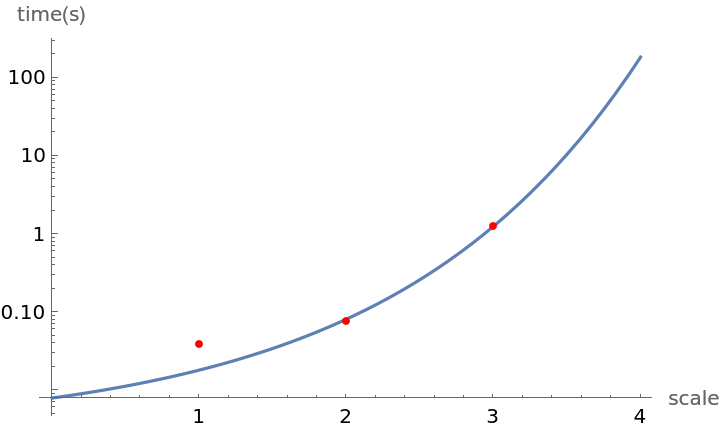 |
Use ArrayMesh to build a maze out of voxels:
| In[8]:= | ![CarpetFractal[n_] := Nest[ArrayFlatten[
{{#, #, #}, {#, 1, #}, {#, #, #}}] &,
{{0, 0, 0}, {0, 1, 0}, {0, 0, 0}}, n]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/35a3dff1b32194f1.png) |
| In[9]:= | ![ArrayMesh[Join[With[
{mazebase = ResourceFunction["RandomSierpinskiMaze"][3][[1, 1, 3 ;; -3, 3 ;; -3]] /. {5 -> 0, 0 -> 1}},
Table[mazebase, {5}]], NestList[RotateRight[Map[
First[Sort@Commonest[Flatten[#][[{2, 4, 6, 8}]]]] &,
Partition[#, {3, 3}, {1, 1}, {1, 1}], {2}], {1, 1}] &,
CarpetFractal[3], 3^3 - 1]][[1 ;; -1 ;; 2]],
ImageSize -> 500, ViewVertical -> {1, 0, 0},
ViewPoint -> 2 {1.5, 1.5, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/212e42288c355abe.png) |
| Out[9]= |  |
Transform output Graph to a knight's walk graph:
| In[10]:= |
| In[11]:= | ![KnightWalkGraph[graph0_] := With[
{knightsMoves = Flatten[Outer[#1@{#2 2, #3 1} &,
{Reverse, Identity}, {1, -1}, {1, -1}], 2]},
Graph[Select[EdgeList[#], GraphDistance[graph0, #[[1]], #[[2]]] == 3 &]] &@
Graph[Union[
Sort /@ Select[Flatten[Outer[UndirectedEdge[#1, #1 + #2] &,
VertexList[maze0], knightsMoves, 1]], MemberQ[VertexList[maze0], #[[2]]] &]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/7792408ee8c10ab8.png) |
| In[12]:= |
| Out[12]= | 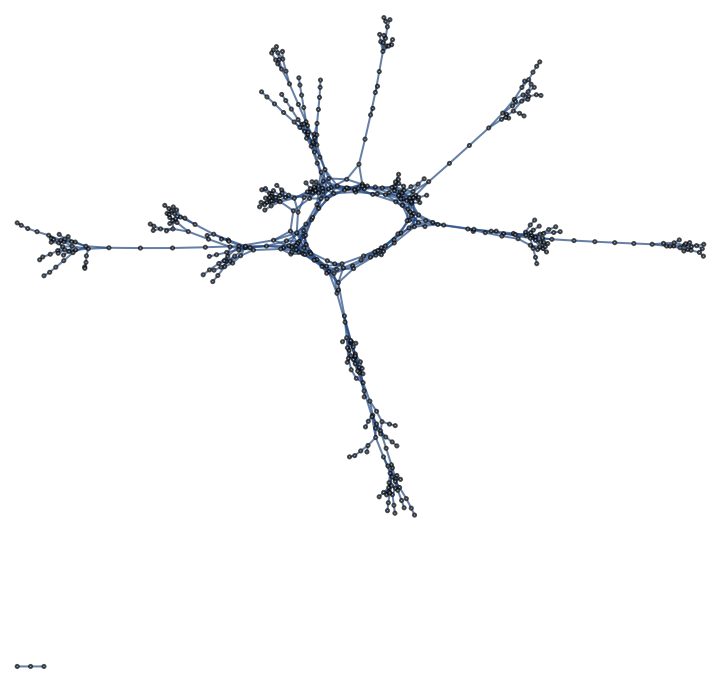 |
Draw the knight's walk Graph over the maze adjacency Graph:
| In[13]:= |
| Out[13]= |  |
Depict a knight's shortest path between corners:
| In[14]:= | ![With[{knightPath = FindShortestPath[kmaze0, {1, 29}, {29, 1}]},
ArrayPlot[ReplacePart[SeedRandom["Compare"];
Reverse[ResourceFunction["RandomSierpinskiMaze"][2][[1, 1]]], Join[
Reverse[# {1, -1} + {1, -1}] -> 2 & /@ Flatten[
FindShortestPath[maze0, #1, #2
][[2 ;; -2]] & @@@ Partition[#, 2, 1], 1],
Reverse[# {1, -1} + {1, -1}] -> 1 & /@ #] &@knightPath],
ColorRules -> {4 -> LightGray, 5 -> White,
0 -> Black, 1 -> Orange, 2 -> LightOrange}]]](https://www.wolframcloud.com/obj/resourcesystem/images/940/940755b8-5a81-4a11-a1ea-e17632753d31/1a6be75f5fbfda83.png) |
| Out[14]= | 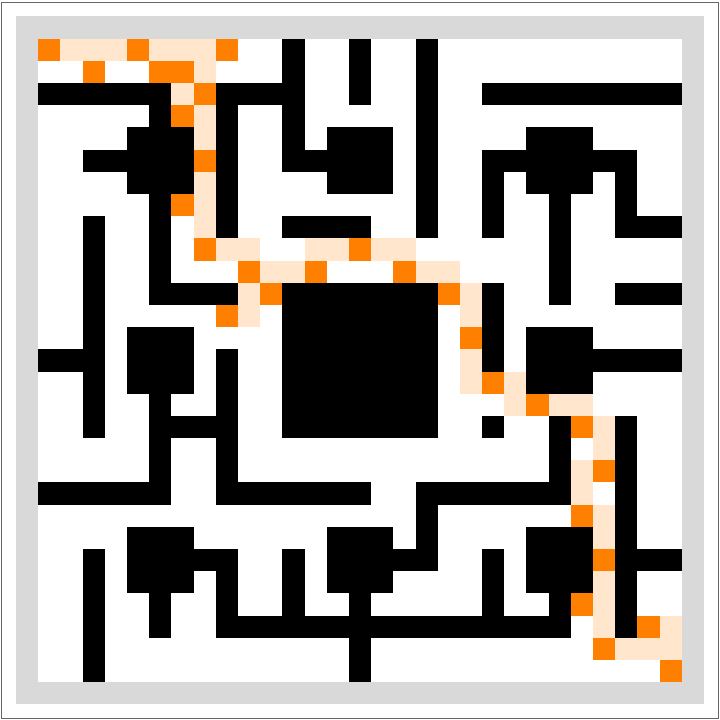 |
This work is licensed under a Creative Commons Attribution 4.0 International License