Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Change an undirected graph into a mixed graph
ResourceFunction["RandomMixedGraph"][{n,m},frac] creates a random graph with n vertices and m edges, with frac of these as directed edges and the rest undirected. | |
ResourceFunction["RandomMixedGraph"][{n,m},frac,spec] creates a table of random graphs with dimensions given by spec. |
Generate a random mixed graph with 20 nodes (vertices) and 48 edges, with a fraction of 0.75 arcs (edges):
| In[1]:= |
| Out[1]= | 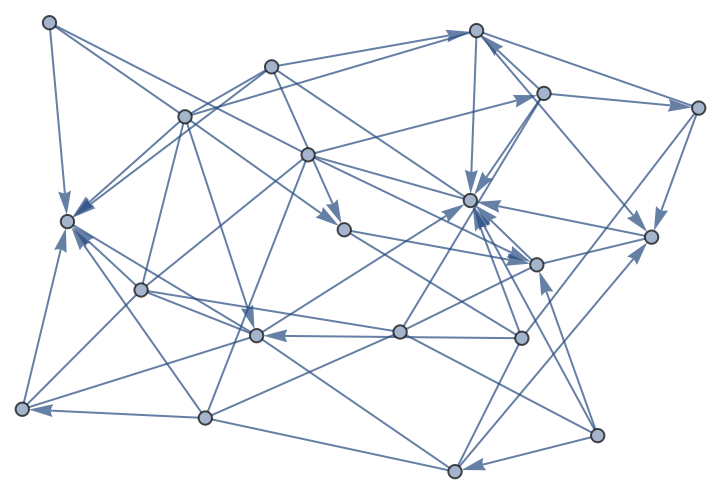 |
Generate a graph with 0.5 directed edges:
| In[2]:= |
| Out[2]= |  |
Generate a list of random mixed graphs:
| In[3]:= |
| Out[3]= |  |
Generate an array of mixed graphs:
| In[4]:= |
| Out[4]= | 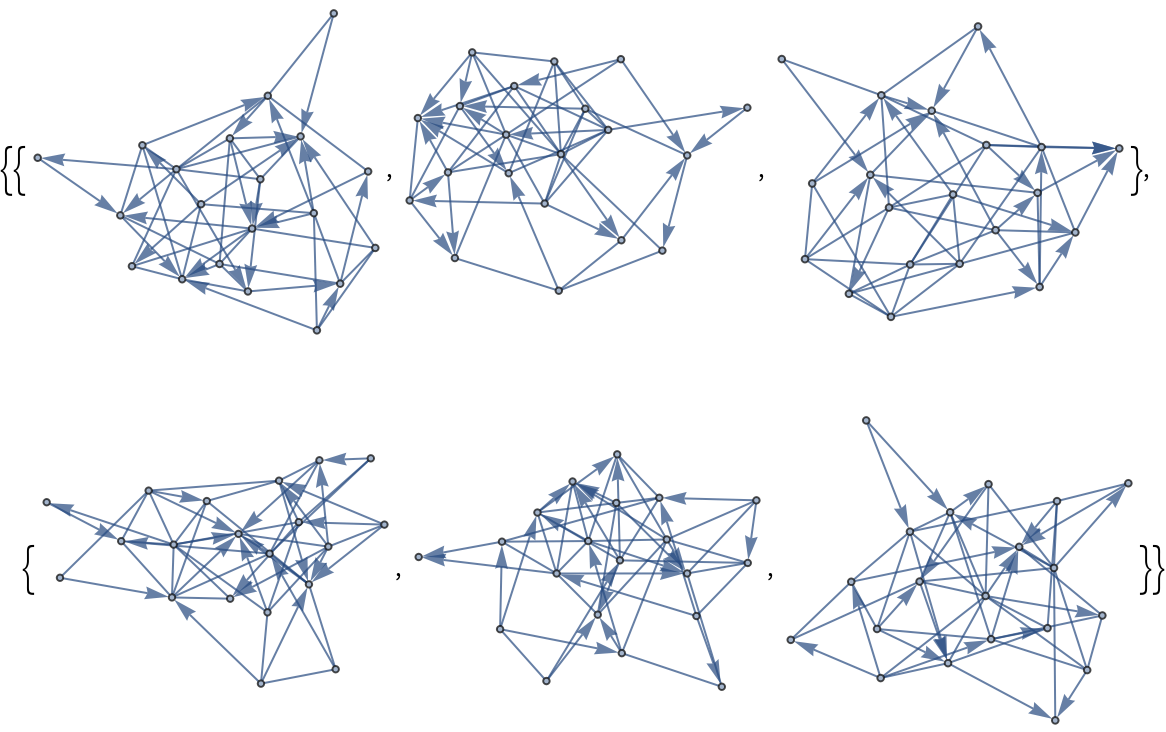 |
Generate a random spatial graph with 148 nodes and 0.68 directed edges:
| In[5]:= |
| Out[5]= |  |
Generate a list of random mixed graphs with the Barabasi-Albert graph distribution:
| In[6]:= |
| Out[6]= | 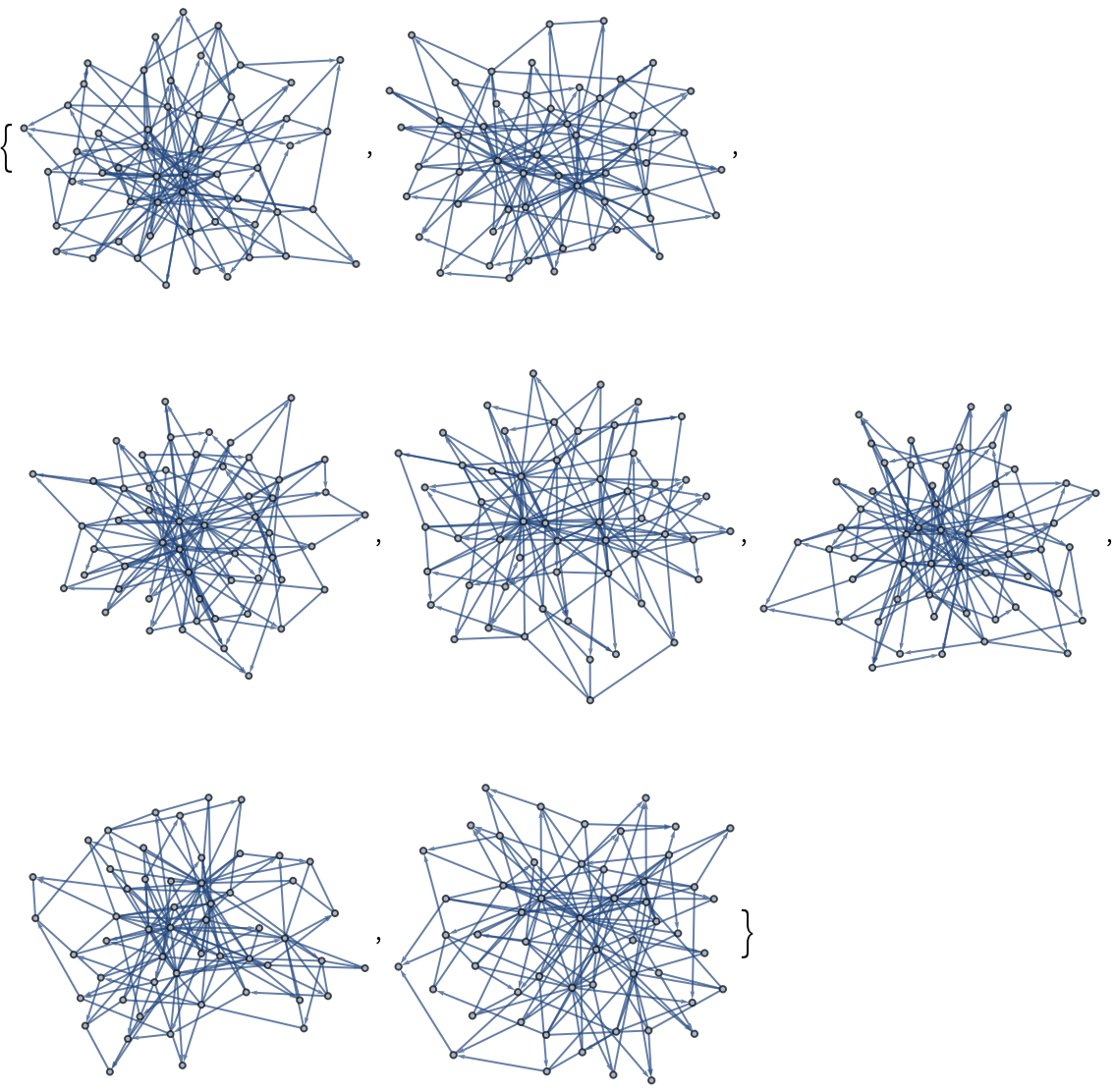 |
Generate a 2x3 array of random graphs based on PriceGraphDistribution:
| In[7]:= |
| Out[7]= | 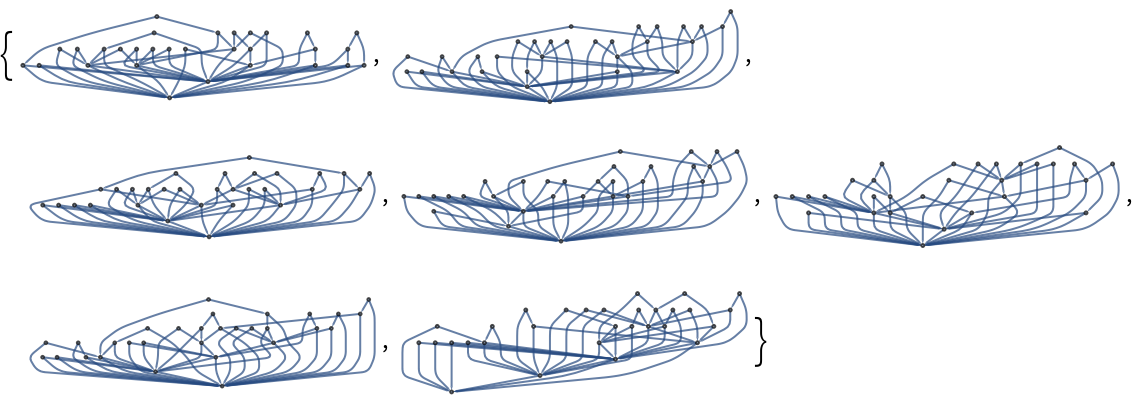 |
Make a big mixed graph:
| In[8]:= |
| Out[8]= |  |
Evaluate if a mixed graph has a Hamiltonian cycle:
| In[9]:= |
| Out[9]= |  |
| In[10]:= |
| Out[10]= |
Find the graph union of two mixed graphs:
| In[11]:= |
| Out[11]= |  |
Make an indexed mixed graph:
| In[12]:= |
| Out[12]= | 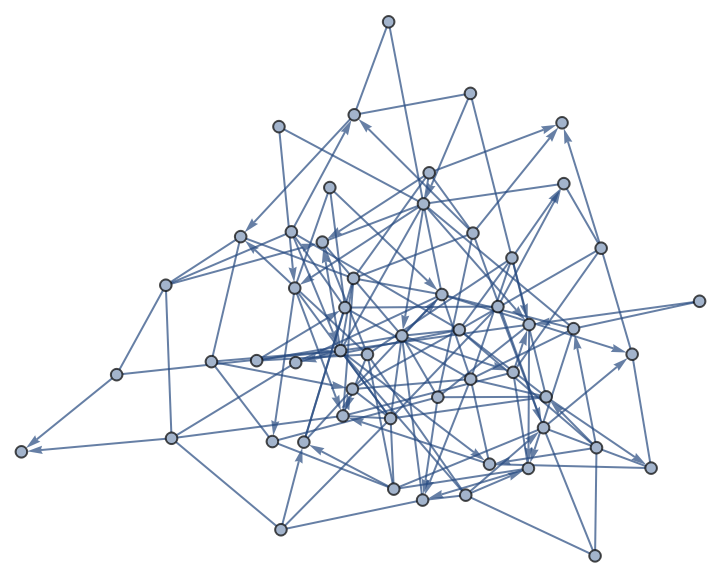 |
Reverse the directed edges of a mixed graph:
| In[13]:= |
| Out[13]= |  |
Compute the graph product for various definitions for two mixed graphs:
| In[14]:= |
| Out[14]= | 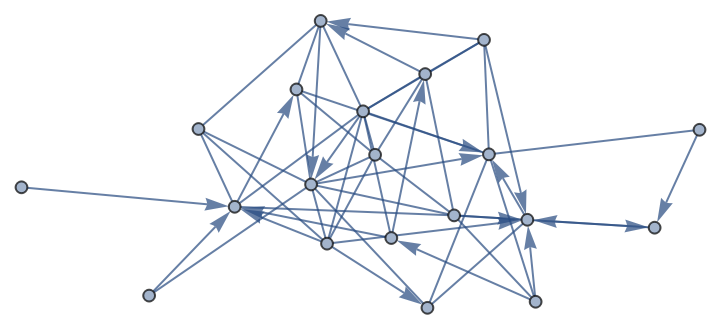 |
| In[15]:= |
| Out[15]= |  |
The graphs can be very very big:
| In[16]:= | ![Table[GraphProduct[\[ScriptCapitalG], \[ScriptCapitalH], op, PlotLabel -> Style[op, 8]], {op, {"Cartesian", "Conormal", "Lexicographical", "Normal", "Rooted", "Tensor"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/1ef/1efaf853-4130-4533-8457-84f83319e155/4706fce52c27033b.png) |
| Out[16]= | 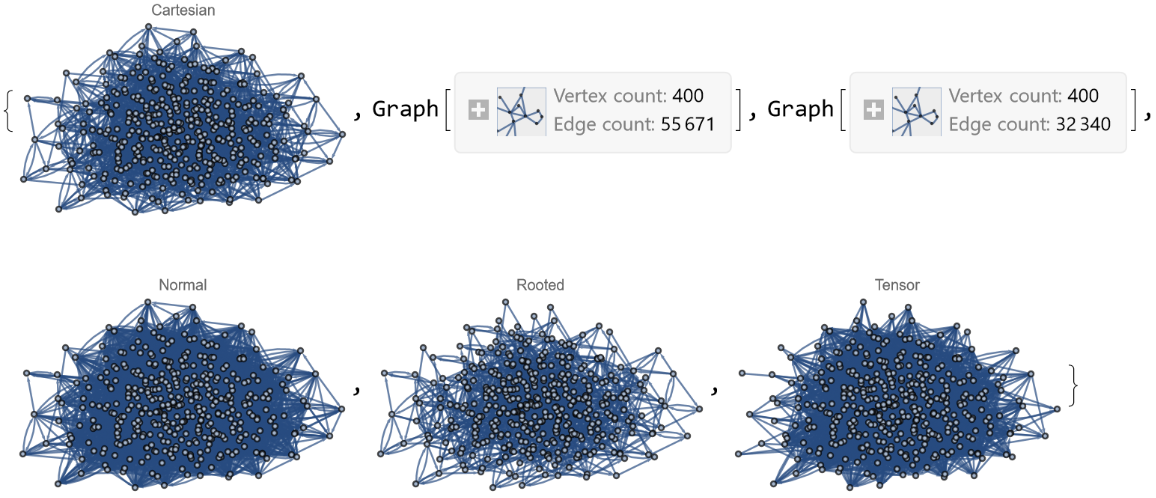 |
Apply binary graph operations to two small mixed graphs:
| In[17]:= |
| Out[17]= | 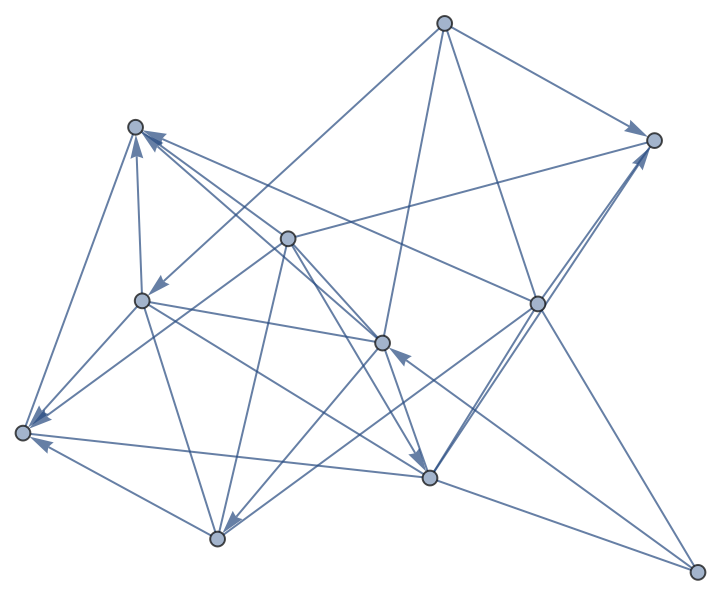 |
| In[18]:= |
| Out[18]= | 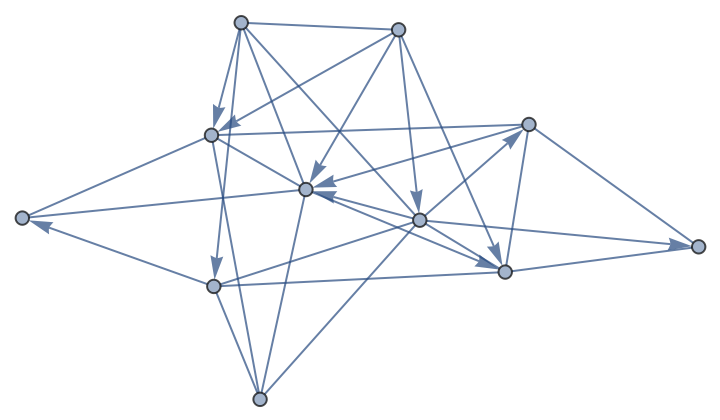 |
| In[19]:= | ![AssociationThread[{"Boolean Graph Xor", "Boolean Graph Nand", "Graph Intersection", "Graph Union", "Graph Difference", "Graph Disjoint Union", "Cartesian Graph Product", "Conormal Graph Product", "Lexicographical Graph Product", "Normal Graph Product", "Rooted Graph Product", "Tensor Graph Product", "Graph Join", "Graph Sum"}, Map[(graphOperation |-> graphOperation[\[ScriptCapitalG], \[ScriptCapitalH]]), {BooleanGraph[Xor, ##] &, BooleanGraph[Nand, ##] &, GraphIntersection,
GraphUnion, GraphDifference, GraphDisjointUnion, GraphProduct[##, "Cartesian"] &, GraphProduct[##, "Conormal"] &, GraphProduct[##, "Lexicographical"] &, GraphProduct[##, "Normal"] &, GraphProduct[##, "Rooted"] &, GraphProduct[##, "Tensor"] &, GraphJoin, GraphSum}]]](https://www.wolframcloud.com/obj/resourcesystem/images/1ef/1efaf853-4130-4533-8457-84f83319e155/2d9e5e50becf1ed4.png) |
| Out[19]= | 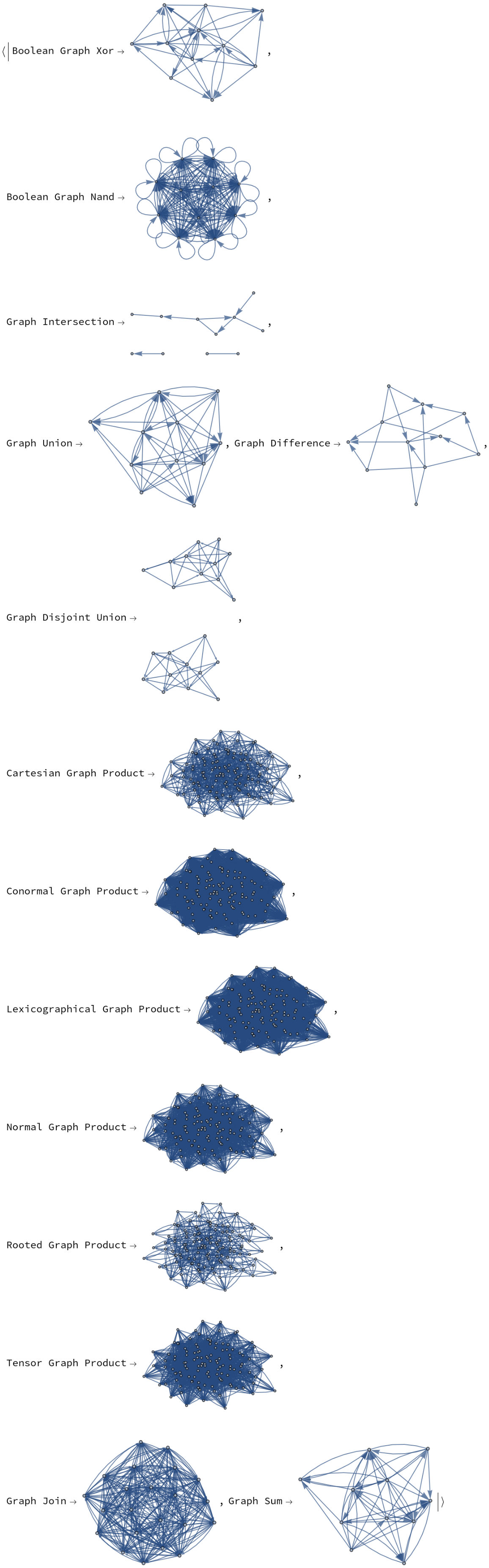 |
Compute unary graph operations on a large random mixed graph:
| In[20]:= |
| Out[20]= |  |
Verify the output of the function produces a mixed graph:
| In[21]:= |
| Out[21]= |
This work is licensed under a Creative Commons Attribution 4.0 International License