Scope (3)
Here are five random (probably-fictitious) metal subgenres:
It may be easier to read as a Column:
Using UpTo provides a different way to get five random (probably-fictitious) metal subgenres:
Here is an array of random (probably-fictitious) metal subgenres:
The nesting is easier to visualize using Grid with the Frame→All option:
Possible Issues (2)
RandomMetalPseudoSubgenre[n] returns unevaluated when n is any data type not mentioned in "Usage":
RandomMetalPseudoSubgenre uses RandomInteger and RandomSample under the hood to create as much randomness as possible. For small samples, this is generally enough to avoid duplicates:
Even so, duplicates may still exist in larger examples:
Neat Examples (6)
While all of the examples are neat, some stand out more than others. For example, sometimes, you get really long subgenre names:
And sometimes, the subgenre names are really short:
On average, however, the lengths of the subgenre names tend to be more average. Experimental evidence suggests that the Mean and Median of the subgenre name lengths are both around 50:
To make metal seem more academic, you can test the Mean/Median hypothesis by using StringLength on longer and longer lists of subgenres. This yields a pair of datasets (where x is the length of the subgenre list and y is the Mean/Median of the corresponding list's string lengths) which seem to support the hypothesis.
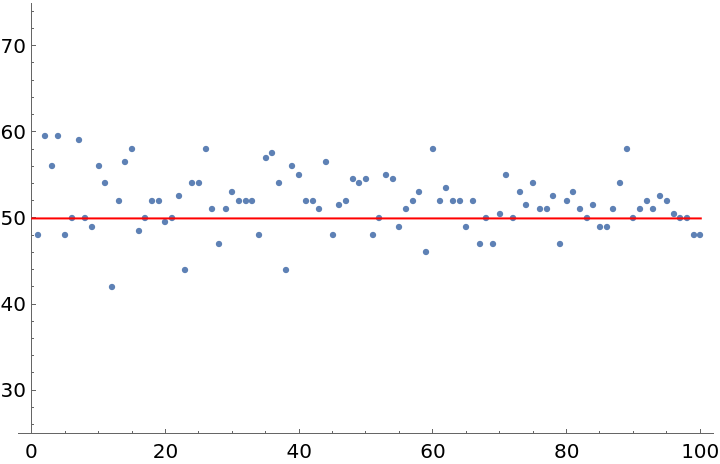
Here is a plot of the corresponding Mean data:
And here is one for the Median data:
The trend can be summarized by taking the Mean of the means and the Median of the medians. Again, the results are very close to 50:




![means = Table[{n, N@Mean[StringLength[
ResourceFunction["RandomMetalPseudoSubgenre"][n]]]}, {n, 1, max1 = 100}];
ListPlot[means, Epilog -> {Red, Line[{{0, 50}, {max1, 50}}]}, PlotRange -> {Automatic, {25, 75}}]](https://www.wolframcloud.com/obj/resourcesystem/images/8dd/8dde8319-947e-4d0f-bc69-5bbcaa0c7530/1da4c56e8a05ad8a.png)
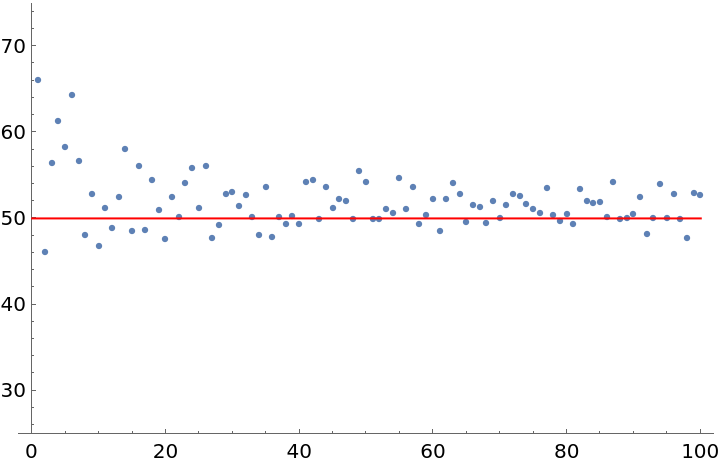
![meds = Table[{n, N@Median[
StringLength[
ResourceFunction["RandomMetalPseudoSubgenre"][n]]]}, {n, 1, max2 = 100}];
ListPlot[meds, Epilog -> {Red, Line[{{0, 50}, {max2, 50}}]}, PlotRange -> {Automatic, {25, 75}}]](https://www.wolframcloud.com/obj/resourcesystem/images/8dd/8dde8319-947e-4d0f-bc69-5bbcaa0c7530/6b2e98a4b698ce81.png)