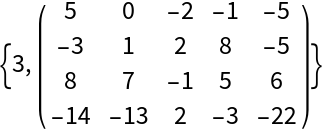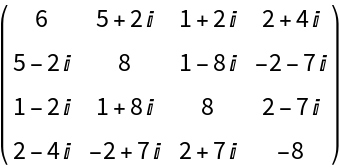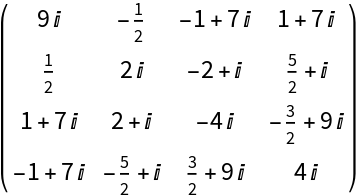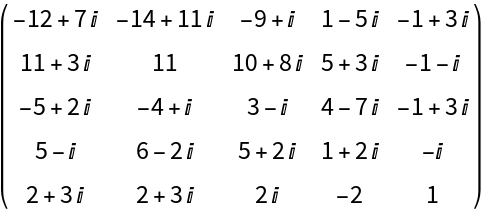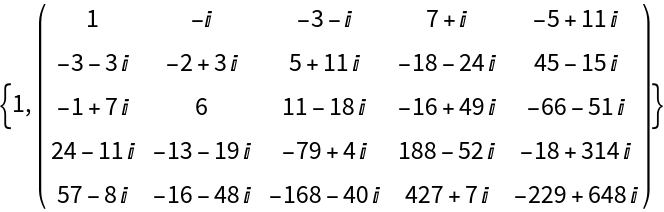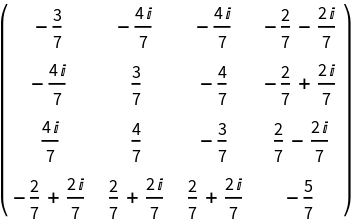Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RandomMatrix

Source Notebook

Get a pseudorandom matrix of a given kind, type and size

Contributed by: Dennis M Schneider

ResourceFunction["RandomMatrix"][type,range,n]

returns an n×n matrix with entries Random[type,range].

ResourceFunction["RandomMatrix"][type,range,{m,n}]

returns an m×n matrix with entries Random[type,range].

ResourceFunction["RandomMatrix"][Complex,range,n]]

returns an n×n matrix with entries RandomComplex[range,n].

ResourceFunction["RandomMatrix"][Complex,range,{m,n}]]

returns an m×n matrix with entries RandomComplex[range,{m,n}].

ResourceFunction["RandomMatrix"][GaussianInteger,range,n]

returns an n×n matrix with entries Random[Integer, range]+IRandom[Integer, range].

ResourceFunction["RandomMatrix"][GaussianInteger,range,{m,n}]

returns an m×n matrix with entries Random[Integer, range]+IRandom[Integer, range].

ResourceFunction["RandomMatrix"][GaussianRational,range,n]

returns an n×n matrix with entries RandomRational[range]+IRandomRational[range].

ResourceFunction["RandomMatrix"][GaussianRational,range,{m,n}]

returns an m×n matrix with entries RandomRational[range]+IRandomRational[range].

ResourceFunction["RandomMatrix"][kind,type,range,n]

returns an n×n kind matrix with entries generated by Random[type,range].

Details and Options

The type can be Integer, Rational, Real, Complex, "GaussianInteger" or "GaussianRational".
The kinds of square matrices allowed are: "Hermitian", "Idempotent", "Involution", "Orthogonal", "Reflection", "SkewHermitian", "SkewSymmetric", "Symmetric", "IdempotentSymmetric", "Reflection", "Triangular", "Unimodular", and "Unitary".
For matrices of kind “Idempotent” or “IdempotentSymmetric”, setting the option “Rank” → k will choose a matrix of that kind having rank k.
The type and range specificaions only specify the type and range of the data used to generate the random matrix, not necessairly the type and range of the resulting matrix.

Examples

Basic Examples (6) 

A random 2×3 real matrix generated by real numbers between 0 and 1:

In[1]:=
ResourceFunction["RandomMatrix"][Real, {0, 1}, {2, 3}] // MatrixForm
Out[1]=

A random 4×5 integer matrix of rank 3 generated by integers between -5 and 10:

In[2]:=
(mat = ResourceFunction["RandomMatrix"][Integer, {-5, 10}, {4, 5}, "Rank" -> 3]); {MatrixRank[mat], MatrixForm[mat]}
Out[3]=

A random 4×4 rational matrix generated by integers between -5 and 10:

In[4]:=
mat = ResourceFunction["RandomMatrix"][Rational, {-5, 10}, 4]; {MatrixRank[mat], MatrixForm[mat]}
Out[5]=

A random 4×5 Gaussian integer matrix of rank 3 generated by Gaussian integers between -5 and 10:

In[6]:=
mat = ResourceFunction["RandomMatrix"][ "GaussianInteger", {-5, 10}, {4, 5}, "Rank" -> 3]; {MatrixRank[mat], MatrixForm[mat]}
Out[7]=

A random 4×5 matrix of rank 3 whose entries are Gaussian rationals generated by integers between -5 and 10:

In[8]:=
mat = ResourceFunction["RandomMatrix"][ "GaussianRational", {-5, 10}, {4, 5}, "Rank" -> 3]; {MatrixRank[mat], MatrixForm[mat]}
Out[9]=

A random 4×4 matrix of rank 2 whose entries are complex numbers generated by RandomComplex[{-5+2I,10-3I}]:

In[10]:=
mat = ResourceFunction["RandomMatrix"][Complex, {-5 + 2 I, 10 - 3 I}, 4, "Rank" -> 2]; {MatrixRank[mat], MatrixForm[mat]}
Out[11]=

Scope (26) 

Examples of special kinds of square matrices:

Triangular (1) 

A random 4×4 upper triangular matrix with integer entries:

In[12]:=
ResourceFunction["RandomMatrix"]["Triangular", Integer, {-5, 5}, 4] // MatrixForm
Out[12]=

Symmetric (2) 

A random 5×5 symmetric matrix with integer entries:

In[13]:=
(mat = ResourceFunction["RandomMatrix"]["Symmetric", Integer, {-2, 2}, 5, "Rank" -> 3]) // MatrixForm
Out[13]=

Check:

In[14]:=
SymmetricMatrixQ[mat]
Out[14]=

AntisymmetricMatrixQ or Skew-Symmetric (2) 

A random 3×3 skew-symmetric matrix with integer entries:

In[15]:=
(mat = ResourceFunction["RandomMatrix"]["SkewSymmetric", Integer, {-3, 5}, 3]) // MatrixForm
Out[15]=

Check:

In[16]:=
AntisymmetricMatrixQ[mat]
Out[16]=

A random 5×5 skew-symmetric matrix with rationals entries:

In[17]:=
(mat = ResourceFunction["RandomMatrix"]["SkewSymmetric", Rational, {-5, 5}, 5]) // MatrixForm
Out[17]=

Check:

In[18]:=
AntisymmetricMatrixQ[mat]
Out[18]=

Hermitian (2) 

A random 4×4 Hermitian matrix with Gaussian integer entries:

In[19]:=
(mat = ResourceFunction["RandomMatrix"]["Hermitian", "GaussianInteger", {-5, 6}, 4]) // MatrixForm
Out[19]=

Check:

In[20]:=
ConjugateTranspose[mat] == mat
Out[20]=

Skew-Hermitian (2) 

A random 4×4 skew-Hermitian matrix with Gaussian integer entries:

In[21]:=
(mat = ResourceFunction["RandomMatrix"]["SkewHermitian", "GaussianInteger", {-5, 9}, 4]) // MatrixForm
Out[21]=

Check:

In[22]:=
ConjugateTranspose[mat] == -mat
Out[22]=

A random 4×4 skew-Hermitian matrix with Gaussian rational entries:

In[23]:=
(mat = ResourceFunction["RandomMatrix"]["SkewHermitian", "GaussianRational", {-5, 9}, 4]) // MatrixForm
Out[23]=

Check:

In[24]:=
ConjugateTranspose[mat] == -mat
Out[24]=

Involution  (2) 

A random 4×4 involution matrix generated by vectors with integer entries and given range specifications:

In[25]:=
(mat = ResourceFunction["RandomMatrix"]["Involution", Integer, {-3, 3}, 4]) // MatrixForm
Out[25]=

Check:

In[26]:=
mat . mat == IdentityMatrix[4]
Out[26]=

Reflection (Symmetric Involution) (4) 

A random 4×4 symmetric involution generated by vectors with integer and range specifications (geometrically these matrices represent orthogonal reflections in the column space of the matrix):

In[27]:=
(matR = ResourceFunction["RandomMatrix"]["Reflection", Integer, {-3, 3}, 4]) // MatrixForm
Out[27]=

Check:

In[28]:=
{SymmetricMatrixQ[matR], matR . matR == IdentityMatrix[4]}
Out[28]=

Verify that the column space is an invariant subspace:

In[29]:=
basiscolumnspace = ResourceFunction["ColumnSpaceBasis"][matR + IdentityMatrix[4]]
Out[29]=
In[30]:=
matR . # & /@ basiscolumnspace
Out[30]=

Verify that vectors orthogonal to the column space are taken into their negatives:

In[31]:=
nullspace = NullSpace[basiscolumnspace]
Out[31]=
In[32]:=
matR . # & /@ nullspace
Out[32]=

Idempotent Symmetric (orthogonal projections) (2) 

A random 4×4 Idempotent symmetric matrix generated by vectors with integer entries (geometrically these matrices represent orthogonal projections onto the column space of the matrix):

In[33]:=
(matP = ResourceFunction["RandomMatrix"]["IdempotentSymmetric", Integer, {-3, 3}, 4]) // MatrixForm
Out[33]=

Check:

In[34]:=
{MatrixRank[matP], matP . matP == matP, matP == Transpose[matP]}
Out[34]=

A random 6×6 idempotent symmetric matrix that represent the orthogonal projections onto a 4 dimensional subspace of the column space of the matrix):

In[35]:=
(matP = ResourceFunction["RandomMatrix"]["IdempotentSymmetric", Integer, {-1, 2}, 6, "Rank" -> 4]) // MatrixForm
Out[35]=
In[36]:=
{MatrixRank[matP], matP . matP == matP, matP == Transpose[matP]}
Out[36]=

Idempotent (2) 

A random 5×5 idempotent matrix generated by vectors with integer entries:

In[37]:=
(matP = ResourceFunction["RandomMatrix"]["Idempotent", Integer, {-1, 3}, 5]) // MatrixForm
Out[37]=

Check:

In[38]:=
{MatrixRank[matP], matP . matP == matP}
Out[38]=

A random 7×7 rank 5 idempotent matrix generated by vectors with integer entries:

In[39]:=
(matP = ResourceFunction["RandomMatrix"]["Idempotent", Integer, {-1, 2}, 7, "Rank" -> 5]) // MatrixForm
Out[39]=
In[40]:=
{MatrixRank[matP], matP . matP == matP}
Out[40]=

Orthogonal (2) 

A random 5×5 orthogonal matrix generated by vectors with integer entries:

In[41]:=
(mat = ResourceFunction["RandomMatrix"]["Orthogonal", Integer, {-1, 2}, 5]) // MatrixForm
Out[41]=

Check:

In[42]:=
Transpose[mat] . mat == IdentityMatrix[5]
Out[42]=

Unimodular (Integer matrix with an integer inverse) (2) 

A random 5×5 unimodular matrix with integer entries:

In[43]:=
(mat = ResourceFunction["RandomMatrix"]["Unimodular", Integer, {-3, 3}, 5]) // MatrixForm
Out[43]=

Check that the determinant is a unit and that the inverse has integer entries:

In[44]:=
{Det[mat], Inverse[mat] // MatrixForm}
Out[44]=

A random 5×5 unimodular matrix with Gaussian integer entries and a Gaussian integer inverse:

In[45]:=
(mat = ResourceFunction["RandomMatrix"]["Unimodular", "GaussianInteger", {-2, 3}, 5]) // MatrixForm
Out[45]=

Check that the determinant is a unit and that the inverse has Gaussian integer entries:

In[46]:=
{Det[mat], Inverse[mat] // MatrixForm}
Out[46]=

Unitary (3) 

A random 4×4 unitary matrix generated by vectors with Gaussian integer entries:

In[47]:=
(matP = ResourceFunction["RandomMatrix"]["Unitary", "GaussianInteger", {-1, 1}, 4]) // MatrixForm
Out[47]=

Check:

In[48]:=
matP . ConjugateTranspose[matP] == IdentityMatrix[4] // Simplify
Out[48]=

A random 4×4 unitary matrix with complex entries:

In[49]:=
(matP = ResourceFunction["RandomMatrix"]["Unitary", Complex, {-1 + 2 I, 1 - 3 I}, 4]) // MatrixForm
Out[49]=

Check:

In[50]:=
matP . ConjugateTranspose[matP] - IdentityMatrix[4] // Chop
Out[50]=

A random 4×4 unitary matrix with complex entries:

In[51]:=
(matP = ResourceFunction["RandomMatrix"]["Unitary", Complex, {-1 + 2 I, 1 - 3 I}, 4]) // MatrixForm
Out[51]=

Check:

In[52]:=
matP . ConjugateTranspose[matP] - IdentityMatrix[4] // Chop
Out[52]=

Publisher

Dennis M Schneider

Version History

  • 2.0.0 – 21 August 2023
  • 1.0.0 – 08 January 2021

Source Metadata

  • Citation:
    Thanks to Jan Mangaldan and yude zhu for pointing out an error.

Related Resources

License Information