Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RandomDyckWord

Source Notebook

Generate a pseudorandom Dyck word

Contributed by: Phileas Dazeley-Gaist

ResourceFunction["RandomDyckWord"][n]

gives a pseudorandom Dyck word with n bracket pairs.

ResourceFunction["RandomDyckWord"][n,k]

gives k pseudorandom Dyck words with n bracket pairs.

Details

A Dyck word is a balanced sequence of brackets where each open bracket has a matching close bracket, and no prefix of the sequence has more close brackets than open brackets.
ResourceFunction["RandomDyckWord"][n] will yield a 2n character word.
A proper set of brackets is defined by three conditions: (1)[] is a proper set; (2) two proper sets can be concatenated; and (3) a proper set can be placed anywhere inside another proper set.

Examples

Basic Examples (2) 

Generate a pseudorandom Dyck word of length 2×10:

In[1]:=
ResourceFunction["RandomDyckWord"][10]
Out[1]=

Generate 10 pseudorandom Dyck words of length 2×5:

In[2]:=
ResourceFunction["RandomDyckWord"][5, 10]
Out[2]=

Applications (3) 

Generate and plot a random Dyck path:

In[3]:=
ListLinePlot[ Prepend[ Accumulate[ ReplaceAll[ Characters[ResourceFunction["RandomDyckWord"][10]], {"[" -> 1, "]" -> -1}]], 0], Filling -> Bottom]
Out[3]=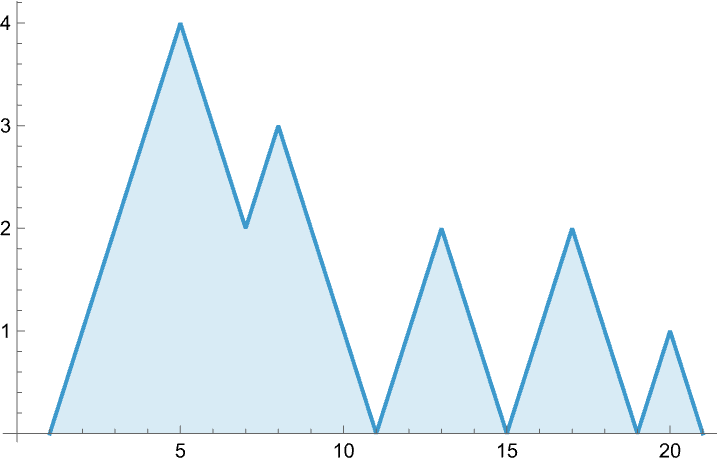

Construct a binary tree from a random Dyck word:

In[4]:=
dyckWordBinaryTree[word_] := Module[ {g = Graph[{0}, {}, VertexLabels -> "Name"], i = 1, pos = 0, unmachedOpenStack = {}, newEdge, newG}, newG = g; GraphTree[Fold[ (Which[ #2 === "[", (AppendTo[unmachedOpenStack, pos \[UndirectedEdge] i]; pos = i; newG = EdgeAdd[#1, Last[unmachedOpenStack]]), #2 === "]", (pos = First[Last[unmachedOpenStack]]; newG = EdgeAdd[#1, pos \[UndirectedEdge] i]; pos = i; unmachedOpenStack = Most[unmachedOpenStack]), True, #1]; ++i; newG) &, g, Characters[word]], 0]]
In[5]:=
SeedRandom[1]; word = ResourceFunction["RandomDyckWord"][4]; dyckWordBinaryTree[word]
Out[7]=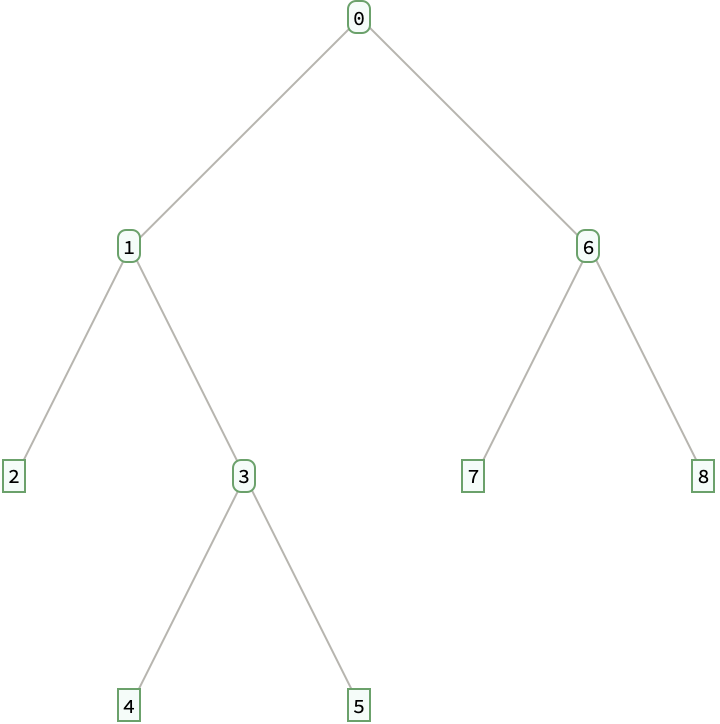

Visualize the nested structure of a random Dyck word as a tree:

In[8]:=
Module[{word = ResourceFunction["RandomDyckWord"][10], counter = 1}, TreeMap[counter++ &, ExpressionTree[ ToExpression[ StringReplace[ "{" <> StringReplace[word, {"[" -> "{", "]" -> "}"}] <> "}", "}{" -> "},{"]]], TreeTraversalOrder -> "BreadthFirst"]]
Out[8]=

Properties and Relations (1) 

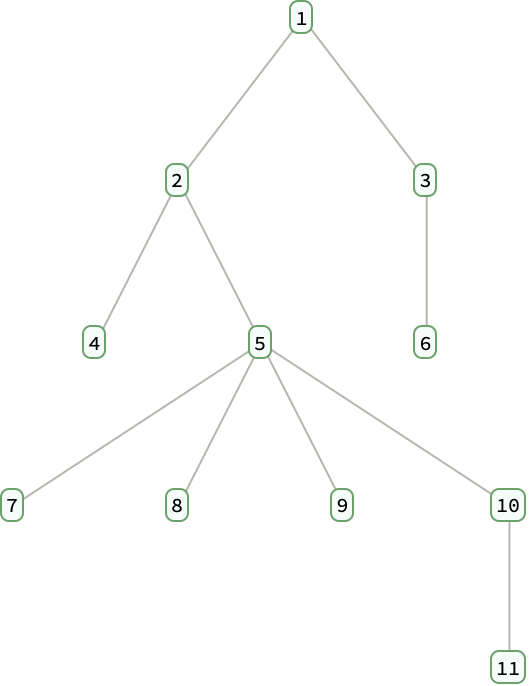RandomDyckWord[n] is equivalent to ToString[ResourceFunction["RandomCombinator"][n+1],{""}]

In[9]:=
(SeedRandom[0]; ResourceFunction["RandomDyckWord"][5]) === (SeedRandom[0]; ToString[ResourceFunction[ ResourceObject[<|"Name" -> "RandomCombinator", "ShortName" -> "RandomCombinator", "UUID" -> "aaf27282-4dad-4601-8691-69fb2710240c", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Generate a pseudorandom combinator", "RepositoryLocation" -> URL[ "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$36a580666aa94703aedfbaf66348059f`RandomCombinator", "FunctionLocation" -> CloudObject[ "https://www.wolframcloud.com/obj/6ea4723c-b164-47f7-8cd6-4da9e1a3ef45"]|>, {ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"}]][5 + 1, {""}]])
Out[9]=

Neat Examples (3) 

Interpret a Dyck word as a sequence of functions to be composed with the initial argument x:

In[10]:=
word = ResourceFunction["RandomDyckWord"][5]
Out[10]=
In[11]:=
(Composition @@ ReplaceAll[Characters[word], {"[" -> f, "]" -> g}]) @@ {x}
Out[11]=

Generate and plot a set of Dyck paths that collectively traverse all possible edges in the lattice of Dyck paths of length 2n:

In[12]:=
With[{n = 10}, ListLinePlot[Map[Prepend[Accumulate[#], 0] &, ReplaceAll[ Characters[NestList[ StringReplace[#, "[]" -> "]["] &, StringJoin[Flatten[Transpose[Array[{"[", "]"} &, n]]]], n - 1]], {"[" -> 1, "]" -> -1}]]]]
Out[12]=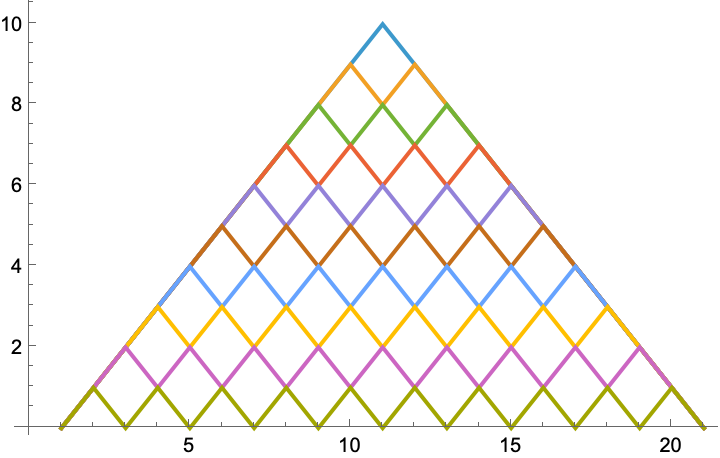

Visualize the distribution of random Dyck paths:

In[13]:=
Module[{dyckWordLength = 10, sampleSize = 1000, dyckWordSample, counts}, dyckWordSample = Table[Prepend[ Accumulate[ ReplaceAll[ Characters[ ResourceFunction["RandomDyckWord"][dyckWordLength]], {"[" -> 1, "]" -> -1}]], 0], sampleSize]; counts = Counts[Flatten[ Map[Thread[{Range[2 dyckWordLength + 1], #}] &, dyckWordSample], 1]]; Show[ (*Generate and plot a set of Dyck paths that collectively traverse all possible edges in the lattice of Dyck paths of length 2n:*) ListLinePlot[Map[Prepend[Accumulate[#], 0] &, ReplaceAll[Characters[ NestList[ StringReplace[#, "[]" -> "]["] &, StringJoin[ Flatten[Transpose[Array[{"[", "]"} &, dyckWordLength]]]], dyckWordLength - 1]], {"[" -> 1, "]" -> -1}]], PlotStyle -> Directive[Dashed, LightGray], AspectRatio -> True, PlotHighlighting -> None], (*Plot the Dyck paths corresponding to a sample of 1000 Dyck words:*) ListLinePlot[dyckWordSample, PlotStyle -> Directive[Opacity[4/sampleSize], Blue], PlotHighlighting -> None], (*Plot the visitation frequency of Dyck path points in the sample of Dyck words:*) Graphics[{Opacity[.5], Blue, #}] &@ KeyValueMap[Tooltip[Disk[#1, 1/sampleSize #2], #2] &, counts], PlotLabel -> Style["Frequency Analysis of Random Dyck Path Coordinates (n=10)", 14]]] // Rasterize[#, ImageSize -> Large] &
Out[13]=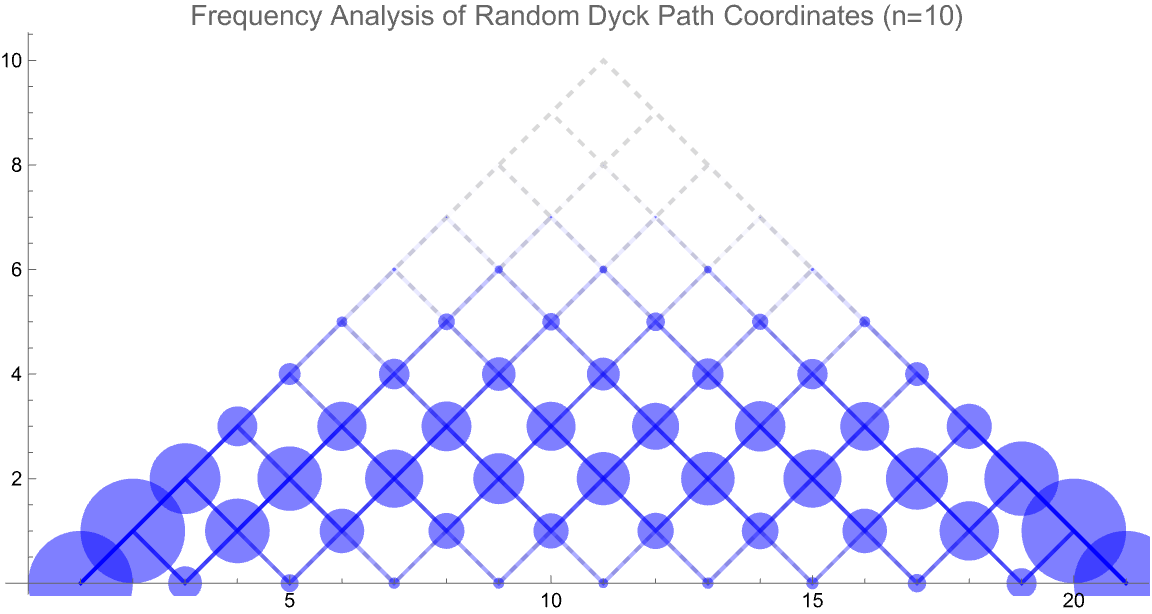

This visualization shows 1000 random Dyck paths of length 20 (10 bracket pairs), with the frequency of visits to each lattice point represented by blue disks of varying sizes. The dashed gray lines show all possible Dyck paths.

Publisher

Phileas Dazeley-Gaist

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 16 June 2025

Related Resources

License Information