Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a random derangement of the numbers 1 through n
ResourceFunction["RandomDerangement"][n] gives a random derangement of the counting numbers 1 through n. |
Get a random derangement of 1,…,10:
| In[1]:= |
| Out[1]= |
Confirm that the result is a derangement:
| In[2]:= |
| Out[2]= |
RandomDerangement is on average linear-time in the number of elements:
| In[3]:= |
| Out[3]= |
Check that successive quotients are all approximately two:
| In[4]:= |
| Out[4]= |
Check that the base-2 logarithms of the timings versus n lie on a line of slope 1:
| In[5]:= |
| Out[5]= | 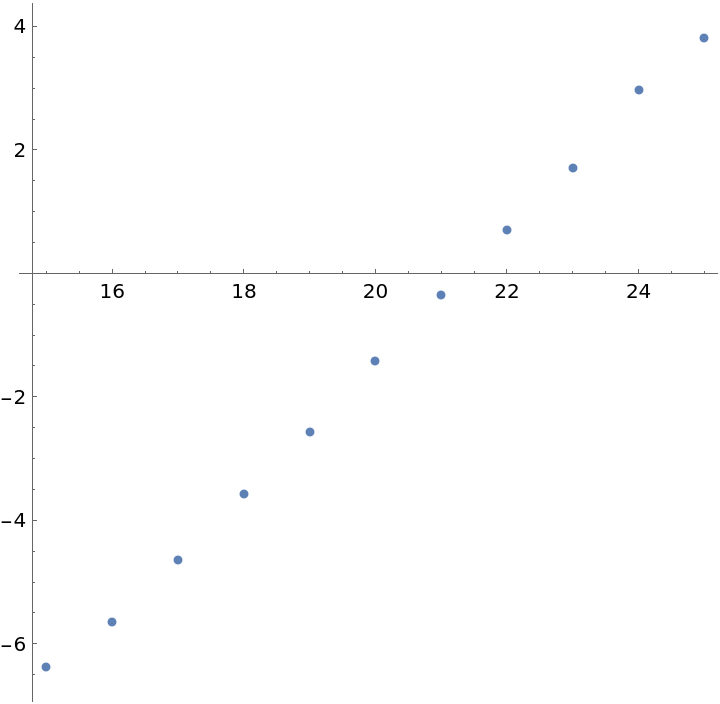 |
This work is licensed under a Creative Commons Attribution 4.0 International License