Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a pseudorandom combinator
ResourceFunction["RandomCombinator"][k] gives a pseudorandom combinator with k symbols. | |
ResourceFunction["RandomCombinator"][k,syms] uses symbols from the list syms. | |
ResourceFunction["RandomCombinator"][k,syms,n] gives a list of n pseudorandom combinators. | |
ResourceFunction["RandomCombinator"][k,syms,{n1,n2,…}] gives an n1×n2×… array of pseudorandom combinators. |
| CombinerFunction | Construct | function to use for combining symbols |
A random combinator with 5 symbols:
| In[1]:= |
| Out[1]= |
Ten random combinators with 5 symbols:
| In[2]:= |
| Out[2]= |
A 3×4 array of random combinators with 5 symbols:
| In[3]:= |
| Out[3]= |
Generate random combinators with any list of symbols:
| In[4]:= |
| Out[4]= |
Generate random combinators of any size:
| In[5]:= |
| Out[5]= |
Use SeedRandom to get repeatable random combinators:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
RandomCombinator generates a uniform distribution. The set of combinators with n symbols from an alphabet of k symbols has cardinality kn×CatalanNumber[n-1]. First compute the cardinality:
| In[9]:= |
| Out[9]= |
Generate 1000 times that number of random combinators and check for a uniform distribution:
| In[10]:= |
| Out[10]= | 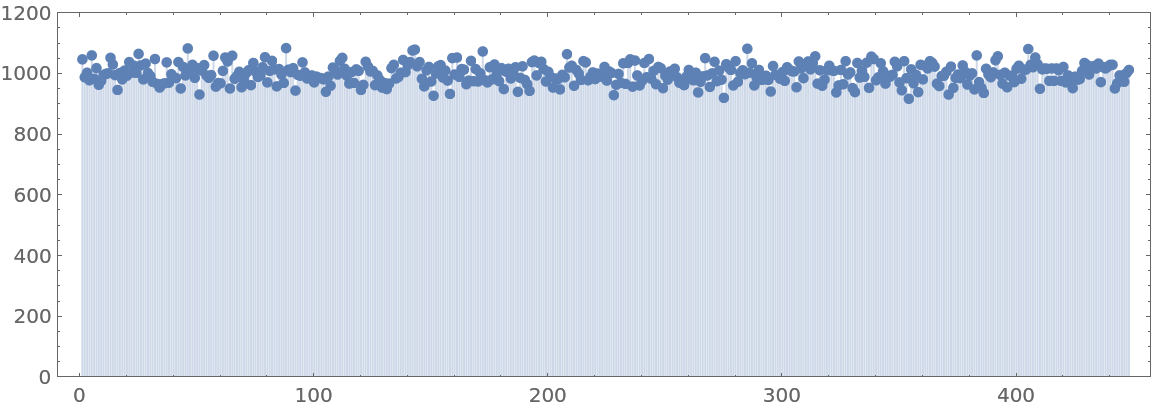 |
This work is licensed under a Creative Commons Attribution 4.0 International License