Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RandomCircleChord

Source Notebook

Generate a random chord of a circle

Contributed by: Sander Huisman

ResourceFunction["RandomCircleChord"][type]

returns a random chord of type type.

ResourceFunction["RandomCircleChord"][type,n]

returns n random chords of type type.

ResourceFunction["RandomCircleChord"][type,n,format]

returns n random chords of type type with the output format format.

Details

ResourceFunction["RandomCircleChord"][] returns a single chord of the type: "TwoPointsOnCircle".
ResourceFunction["RandomCircleChord"][All] returns the list of possibles types type.
The type can be any of the following: "TwoPointsOnCircle", "TwoPointsInCircle", "PointInCircleAngle", "RadiusAngleMidpoint", "PointInCircleMidpoint", "CenterAngle":
The format can be any of the following: "EndPoints", "Line", "Lines", "Midpoints".

Examples

Basic Examples (2) 

Generate a random circle chord:

In[1]:=
ResourceFunction["RandomCircleChord"]["TwoPointsInCircle"]
Out[1]=

Generate 100 random circle chords and visualize:

In[2]:=
ResourceFunction["RandomCircleChord"]["TwoPointsOnCircle", 300] // Graphics
Out[2]=

Scope (6) 

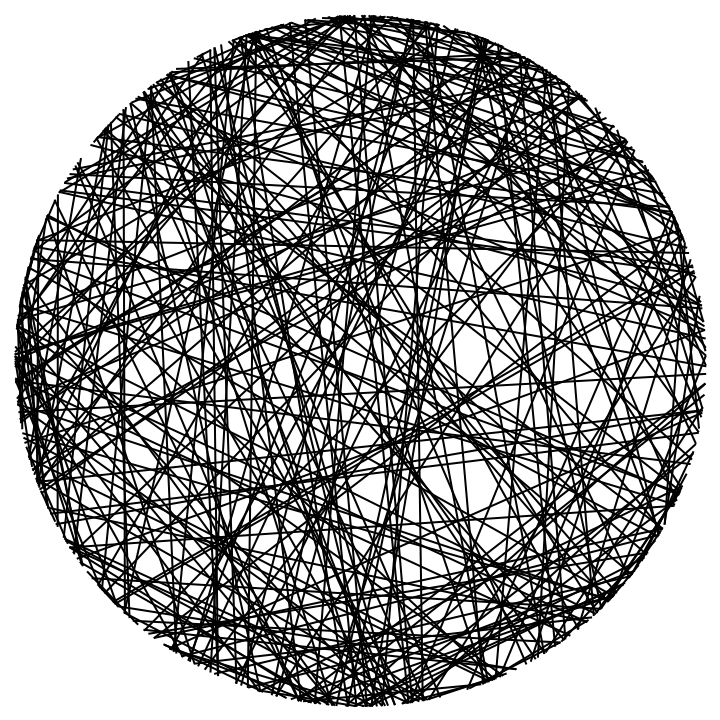Retrieve all types:

In[3]:=
ResourceFunction["RandomCircleChord"][All]
Out[3]=

By default, the chords are returns as a list of Line objects::

In[4]:=
ResourceFunction["RandomCircleChord"]["TwoPointsInCircle", 2]
Out[4]=

Get the endpoints of the chord:

In[5]:=
ResourceFunction[ "RandomCircleChord"]["TwoPointsInCircle", 2, "EndPoints"]
Out[5]=

Represent the chords as a single Line object:

In[6]:=
ResourceFunction["RandomCircleChord"]["TwoPointsInCircle", 2, "Line"]
Out[6]=

Get the midpoints of each chord:

In[7]:=
ResourceFunction[ "RandomCircleChord"]["TwoPointsInCircle", 2, "Midpoints"]
Out[7]=

Generate 50 chords and return a single Line object:

In[8]:=
ResourceFunction["RandomCircleChord"]["PointInCircleMidpoint", 50, "Line"] // Graphics
Out[8]=

Applications (1) 

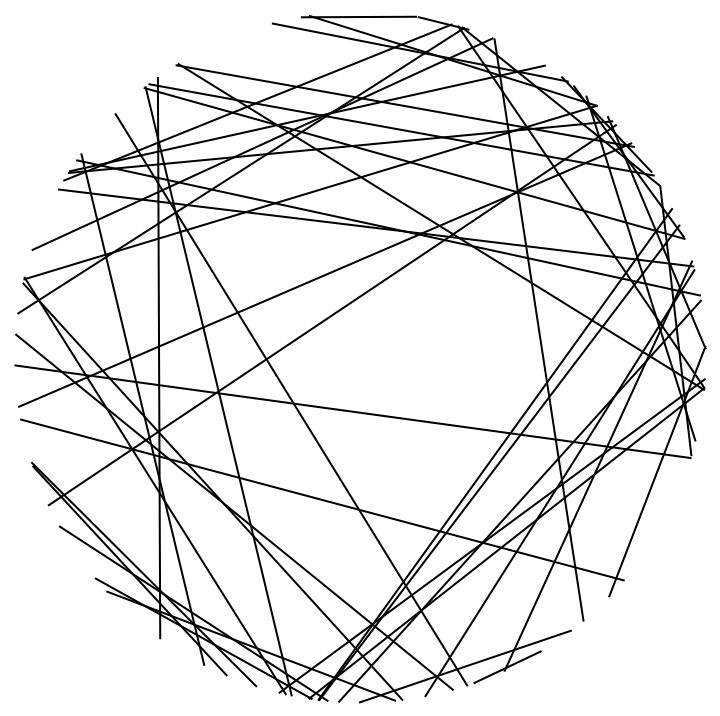Find the chance of each slice of a pie getting a candle given that the two candles are randomly placed and the cake randomly cut:

In[9]:=
n = 50000; Table[ {t, Count[Table[ pts = RandomPoint[Disk[], 2]; {{ch1x, ch1y}, {ch2x, ch2y}} = ResourceFunction["RandomCircleChord"][t, 1, "EndPoints"][[1]]; Graphics[{Point[pts], Line[{{ch1x, ch1y}, {ch2x, ch2y}}], Circle[]}]; booles = (ch2x - ch1x) (#[[2]] - ch1y) - (ch2y - ch1y) (#[[1]] - ch1x) > 0 & /@ pts; booles[[1]] === ! booles[[2]] , {n} ], True]/N[n]} , {t, ResourceFunction["RandomCircleChord"][All]} ] // Grid
Out[10]=

Properties and Relations (1) 

Compare the distribution of midpoints visually:

In[11]:=
types = ResourceFunction["RandomCircleChord"][All]; midpts = Table[ResourceFunction["RandomCircleChord"][t, 1000, "Midpoints"], {t, types}]; {types, Graphics[{Point[#], Circle[]}, ImageSize -> 150] & /@ midpts} // Transpose // Grid
Out[13]=

Neat Examples (2) 

Find the radial distribution of the midpoints:

In[14]:=
types = ResourceFunction["RandomCircleChord"][All]; rs = Table[ Norm /@ ResourceFunction["RandomCircleChord"][t, 100000, "Midpoints"], {t, types}]; {types, Histogram[#, {0, 1, 0.02}, "PDF", ImageSize -> 200, Frame -> True, ImagePadding -> {{20, 10}, {20, 10}}] & /@ rs} // Transpose // Grid
Out[15]=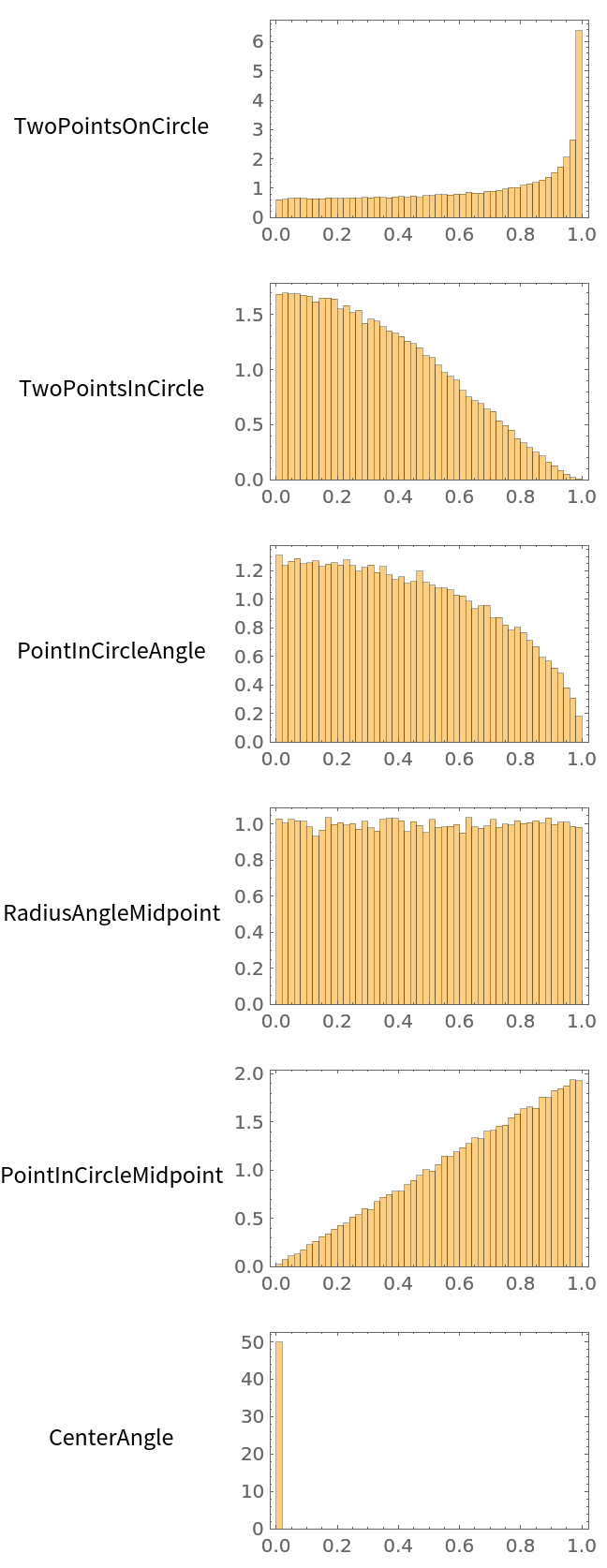

Check the Bertrand paradox for a variety of ways of generating random chords:

In[16]:=
baselen = Norm[First[Differences[CirclePoints[3]]]]; n = 10^5; Table[ out = ResourceFunction["RandomCircleChord"][t, n, "EndPoints"]; out = Norm[#2 - #1] & @@@ out; out -= baselen; {t, Total[UnitStep[out]]/N[n]} , {t, ResourceFunction["RandomCircleChord"][All]} ] // SortBy[Last] // Grid
Out[18]=

Publisher

SHuisman

Version History

  • 1.0.0 – 17 May 2022

License Information