Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a random binary tree
ResourceFunction["RandomBinaryTree"][n] gives a pseudorandom binary tree with n leaf nodes. | |
ResourceFunction["RandomBinaryTree"][n,k] gives a list of k pseudorandom binary trees. | |
ResourceFunction["RandomBinaryTree"][n,{k1,k2,…}] gives a k1×k2×… array of binary trees. |
Generate a random binary tree with 10 leaf nodes:
| In[1]:= |
| Out[1]= | 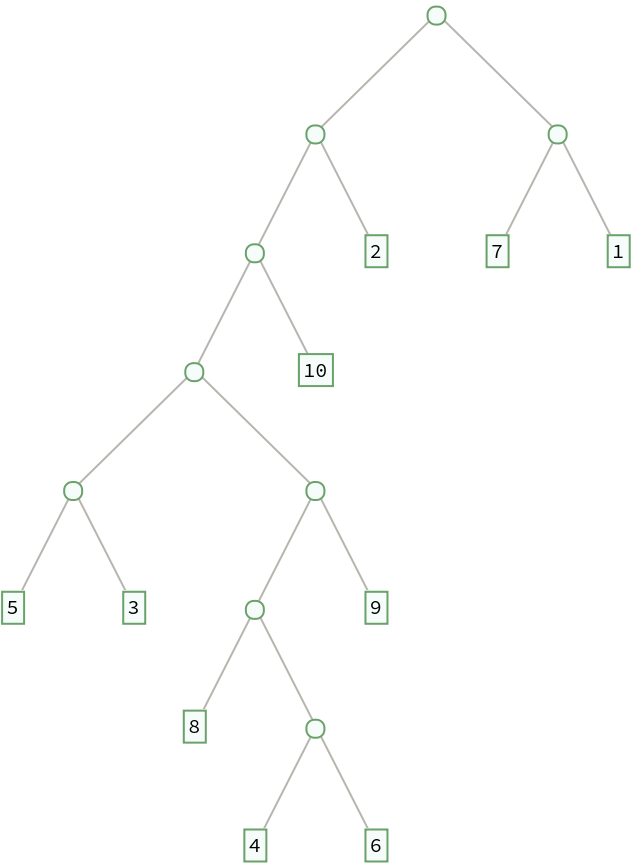 |
Generate a list of random binary trees:
| In[2]:= |
| Out[2]= | 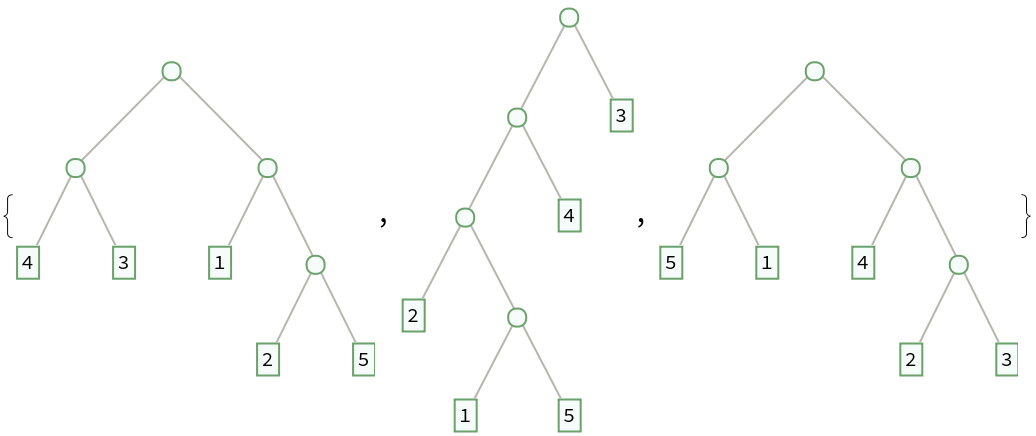 |
Generate an array of random binary trees:
| In[3]:= |
| Out[3]= | 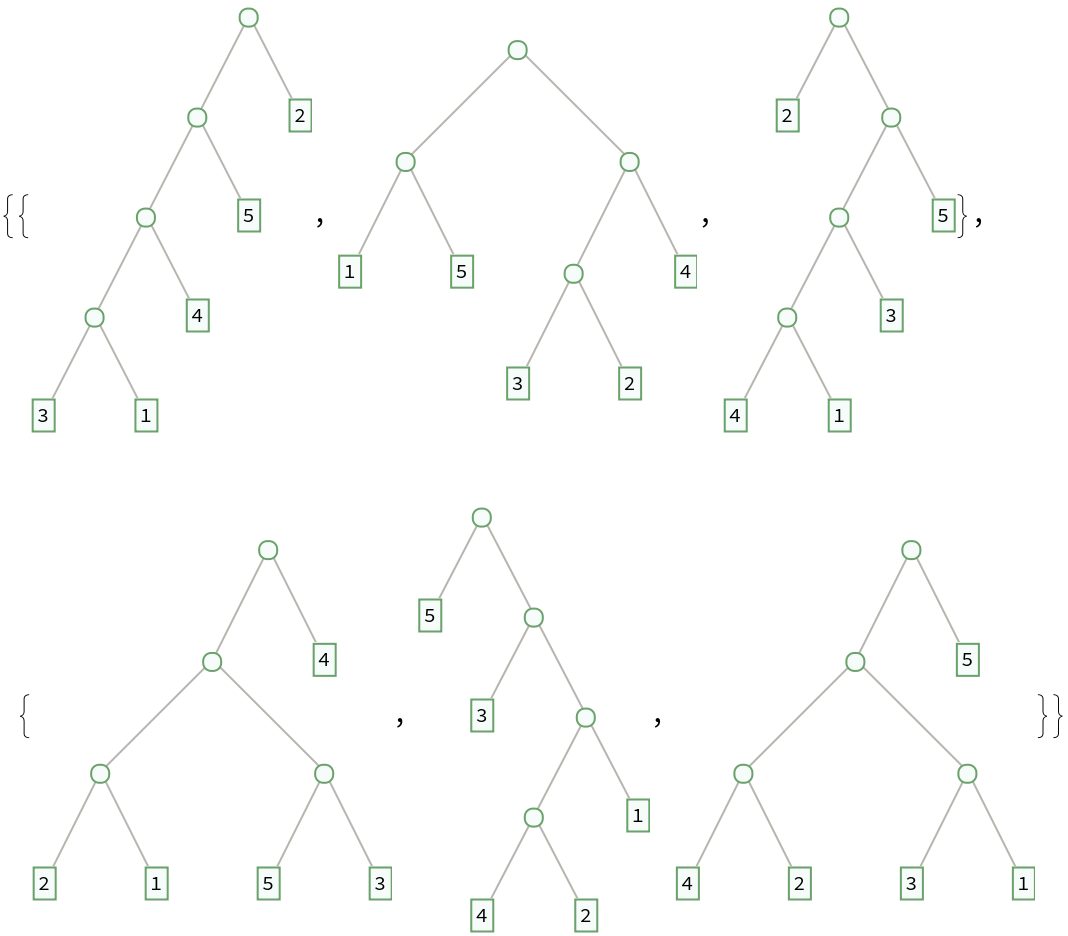 |
RandomBinaryTree uses integer data:
| In[4]:= |
| Out[4]= | 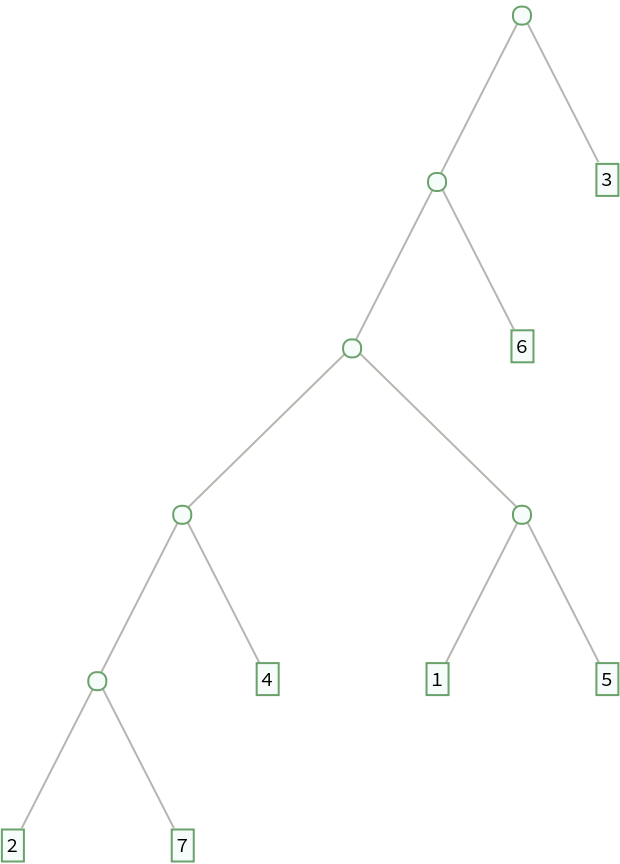 |
Use TreeMap to replace data in the binary tree:
| In[5]:= |
| Out[5]= | 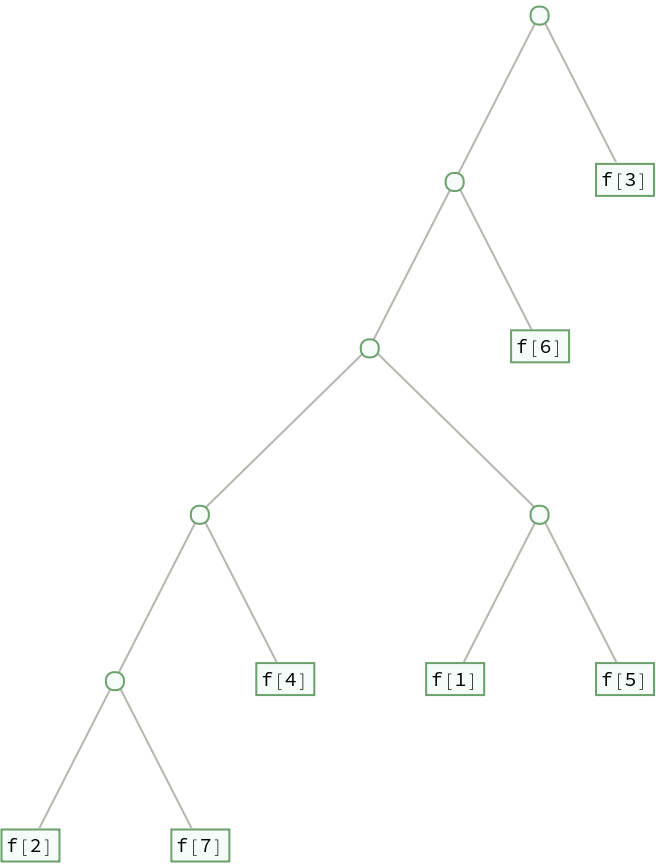 |
RandomBinaryTree gives pseudorandom binary trees:
| In[6]:= |
| Out[6]= | 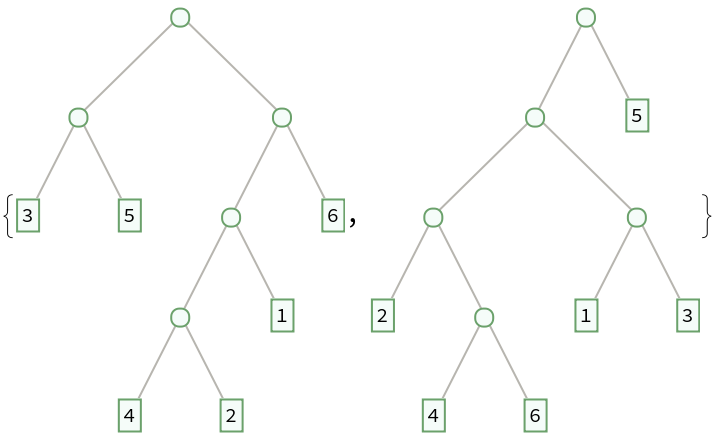 |
Use SeedRandom to get repeatable random binary trees:
| In[7]:= |
| Out[7]= | 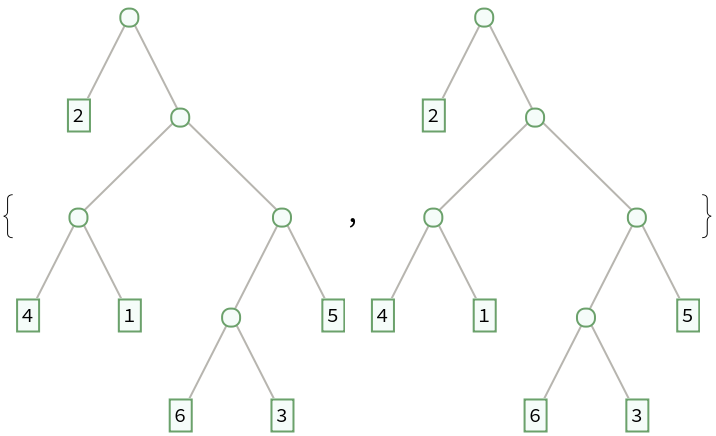 |
Use BlockRandom to block one use of RandomBinaryTree from affecting others:
| In[8]:= |
| Out[8]= | 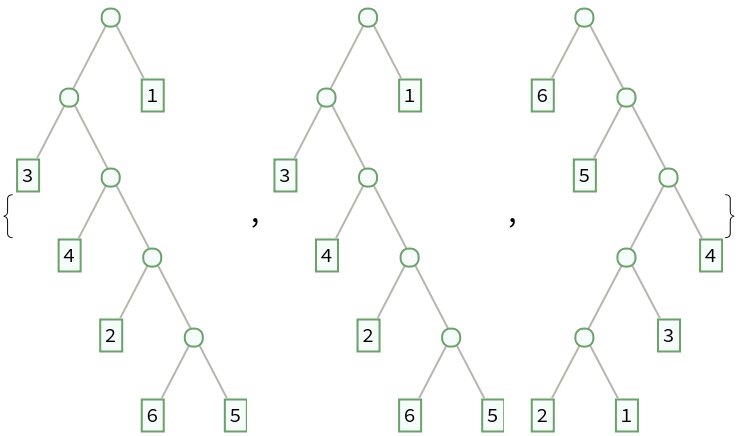 |
RandomBinaryTree[n] can produce n!CatalanNumber[n-1] different binary trees:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 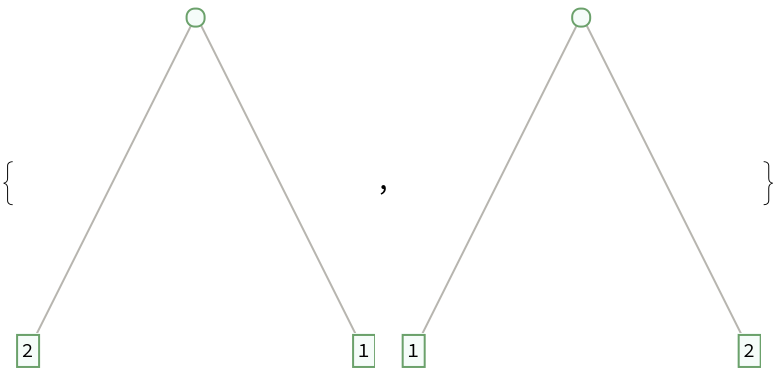 |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
RandomBinaryTree[n] samples from the uniform distribution over the leaf-labeled, rooted, ordered binary trees with n leaf nodes:
| In[14]:= |
| Out[14]= | 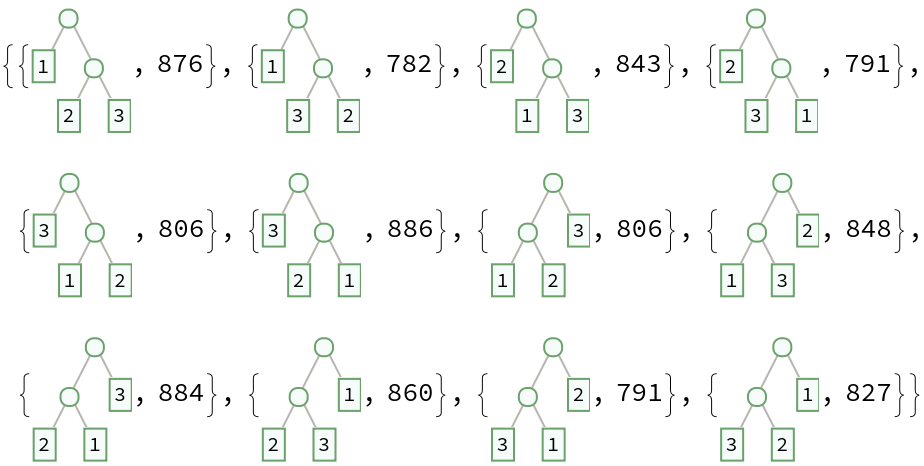 |
This work is licensed under a Creative Commons Attribution 4.0 International License