Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the radical hyperplane of two hyperspheres
ResourceFunction["RadicalHyperplane"][c1,c2] gives the radical hyperplane of the hyperspheres c1 and c2. |
Compute the radical line of two circles:
| In[1]:= | ![c1 = Circle[{0, 0}, 1];
c2 = Circle[{2, 2}, 1/3];
hp = ResourceFunction["RadicalHyperplane"][c1, c2]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/49cc4344bdf2e3fa.png) |
| Out[3]= |
Show the radical line and the two circles:
| In[4]:= |
| Out[4]= | 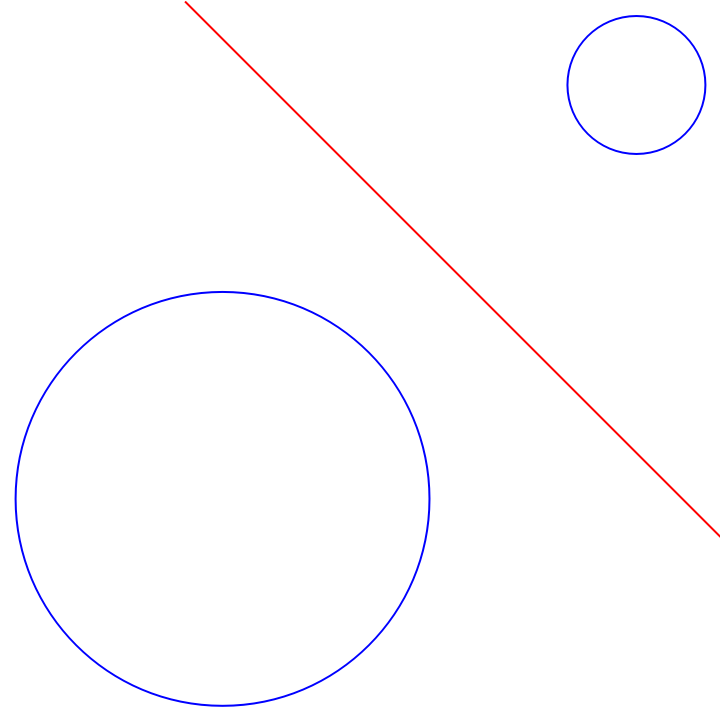 |
Visualize the radical plane of two spheres:
| In[5]:= | ![With[{c1 = Sphere[{0, 0, 0}, 1], c2 = Sphere[{2, 2, 2}, 1/3]}, Graphics3D[{{Blue, c1, c2}, {LightRed, ResourceFunction["RadicalHyperplane"][c1, c2]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/2c2fa5fe55ec80fd.png) |
| Out[5]= | 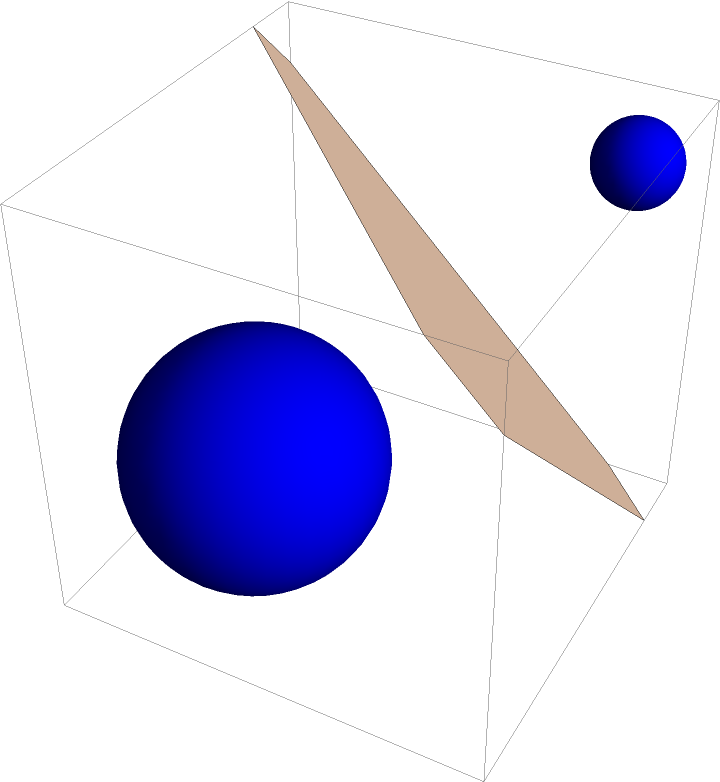 |
The radical line of a circle and a disk:
| In[6]:= | ![With[{c1 = Circle[{0, 0}, 1], c2 = Disk[{2, 2}, 1/3]}, Graphics[{{Blue, c1, c2}, {Red, ResourceFunction["RadicalHyperplane"][c1, c2]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/38f60a32fca9e88e.png) |
| Out[6]= | 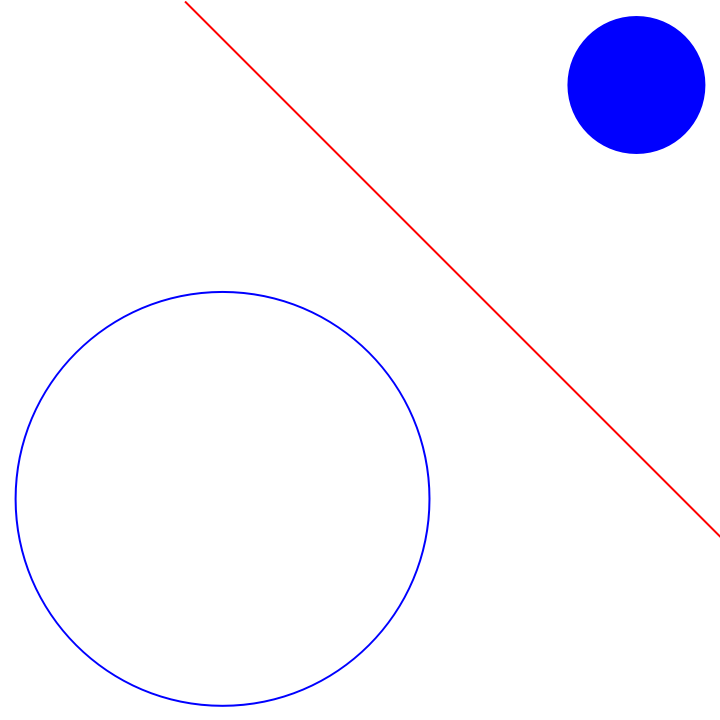 |
The radical plane of a sphere and a ball:
| In[7]:= | ![With[{c1 = Ball[{0, 0, 0}, 1], c2 = Sphere[{2, 2, 2}, 1/3]}, Graphics3D[{{Blue, c1, c2}, {LightRed, ResourceFunction["RadicalHyperplane"][c1, c2]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/1b028a3ecfe39bbf.png) |
| Out[7]= | 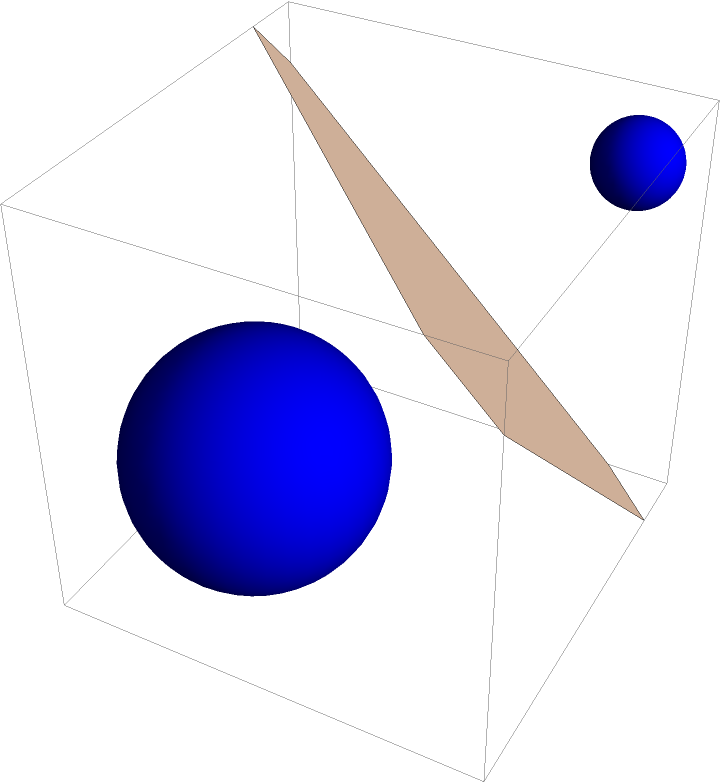 |
A point is treated as a hypersphere with zero radius:
| In[8]:= | ![With[{c1 = Circle[{0, 0}, 1], c2 = Point[{2, 2}]}, Graphics[{{Blue, c1, AbsolutePointSize[5], c2}, {Red, ResourceFunction["RadicalHyperplane"][c1, c2]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/0973e01603b4601e.png) |
| Out[8]= | 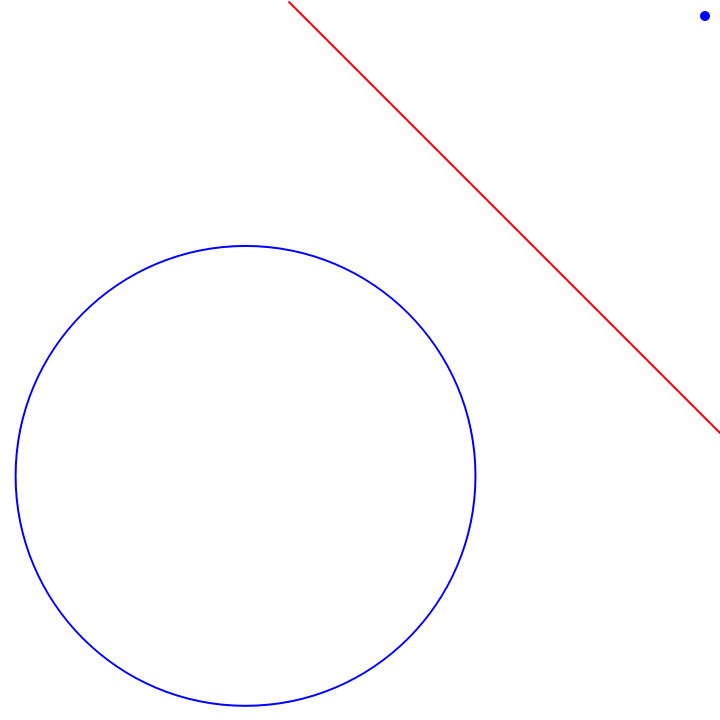 |
Find the tangent through a given point of a circle:
| In[9]:= | ![c1 = Circle[{0, 0}, 1];
p1 = Point[AngleVector[ArcTan[4/3]]];
Graphics[{AbsolutePointSize[5], AbsoluteThickness[1], c1, p1, ResourceFunction["RadicalHyperplane"][c1, p1]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/2516eb2c81c471d9.png) |
| Out[9]= |  |
The radical lines of three circles with noncollinear centers and no two of them concentric, taken two at a time, coincide at the radical center:
| In[10]:= | ![circs = {Circle[{0, 0.1}, 1], Circle[{3, 0}, 0.6], Circle[{1, 3}, 1.2]};
lines = ResourceFunction["RadicalHyperplane"] @@@ Subsets[circs, {2}];
Graphics[{Transpose[{{Red, Blue, Green}, circs, lines}], {AbsolutePointSize[6], RegionIntersection @@ lines}}, PlotRange -> {{-1, 3.7}, {-1, 4.3}}]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/684dcf672634f3f5.png) |
| Out[10]= | 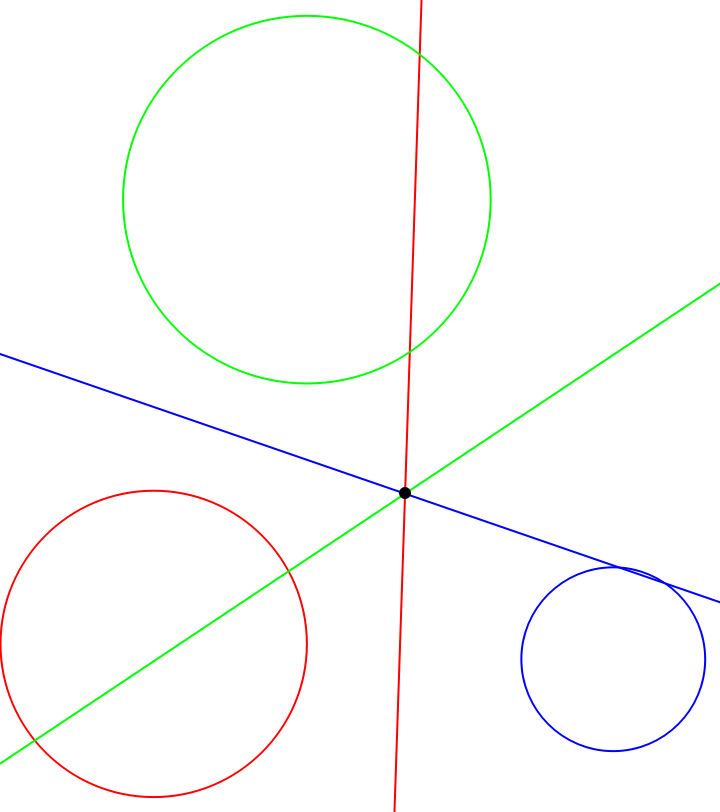 |
If two hyperspheres intersect, the radical hyperplane passes through their intersection:
| In[11]:= | ![With[{c1 = Circle[{0, 0}, 1], c2 = Circle[{1, 1}, 2/3]}, Graphics[{{Blue, c1, c2}, {Red, ResourceFunction["RadicalHyperplane"][c1, c2]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/100f7f179ea1be99.png) |
| Out[11]= |  |
Again in three dimensions:
| In[12]:= | ![With[{c1 = Ball[{0, 0, 0}, 1], c2 = Sphere[{1, 1, 1}, 4/3]}, Graphics3D[{{Opacity[2/5], Blue, c1, c2}, {LightRed, ResourceFunction["RadicalHyperplane"][c1, c2]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/4398e5f61abf898e.png) |
| Out[12]= | 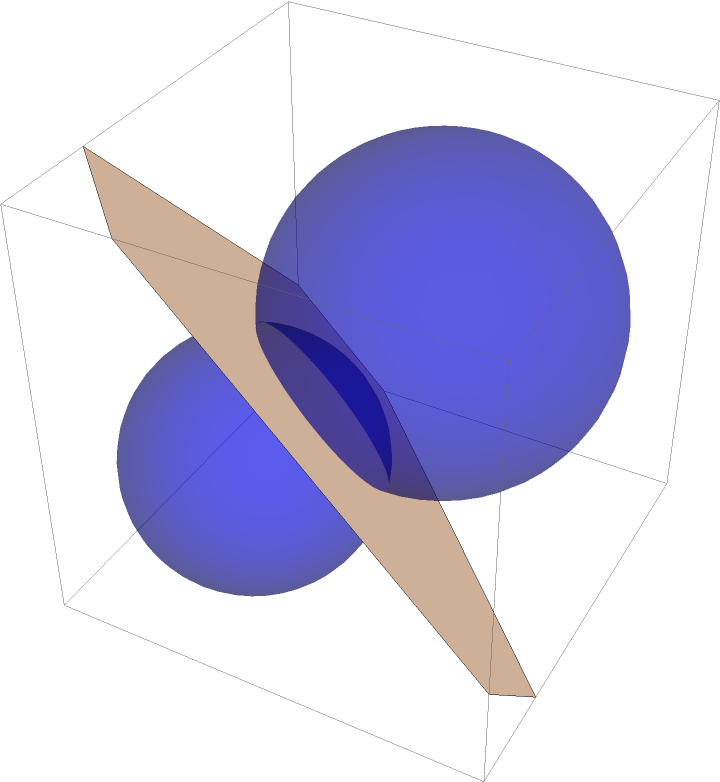 |
The power diagram of two circles is comprised of two half-planes separated by the radical line of the two circles:
| In[13]:= | ![Show[ResourceFunction["PowerDiagram"][{Circle[{0, 0}, 1], Circle[{2, 2}, 1/3]}], Graphics[{Brown, Circle[{0, 0}, 1], Circle[{2, 2}, 1/3], Directive[Dashed, Orange], ResourceFunction["RadicalHyperplane"][Circle[{0, 0}, 1], Circle[{2, 2}, 1/3]]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/4b02cec9b9d9d3a6.png) |
| Out[13]= | 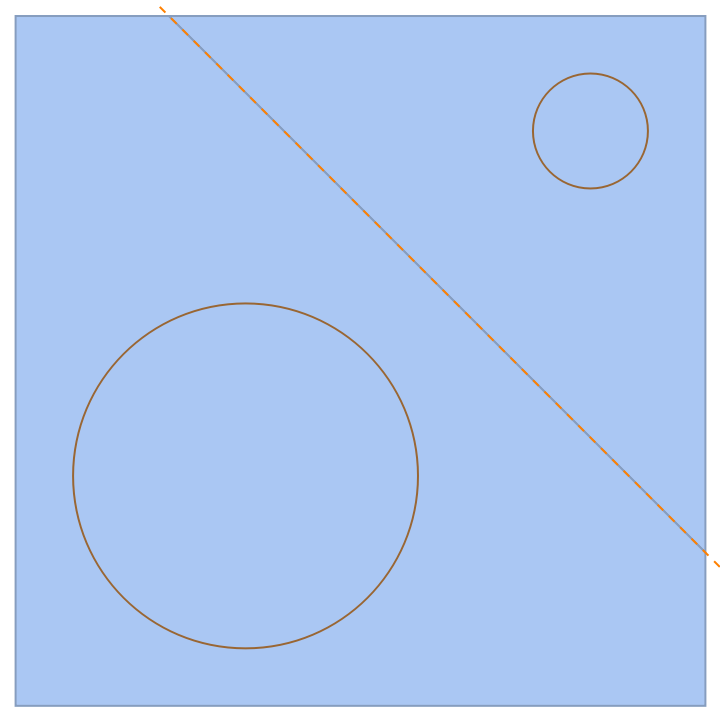 |
RadicalHyperplane is left unevaluated for concentric hyperspheres:
| In[14]:= |
| Out[14]= |
The pairwise radical hyperplanes of four three-dimensional, nonconcentric spheres, with all centers noncoplanar, intersect at a point:
| In[15]:= | ![With[{c1 = Sphere[{0, 0, 0}, 1], c2 = Sphere[{2, 2, 0}, 1/3], c3 = Sphere[{2, 1, 2}, 1/2], c4 = Sphere[{0, 1, 2}, 2/3]},
Graphics3D[{{Blue, c1, c2, c3, c4}, {LightRed, Opacity[0.4], ResourceFunction["RadicalHyperplane"] @@@ Subsets[{c1, c2, c3, c4}, {2}]}, {Red, Sphere[First[
RegionIntersection @@ (ResourceFunction["RadicalHyperplane"] @@@
Subsets[{c1, c2, c3, c4}, {2}])], 0.05]}}, Boxed -> False]]](https://www.wolframcloud.com/obj/resourcesystem/images/e58/e58084fe-c428-4f4c-952f-d3789578ffa3/2e778a9975d6fd11.png) |
| Out[15]= | 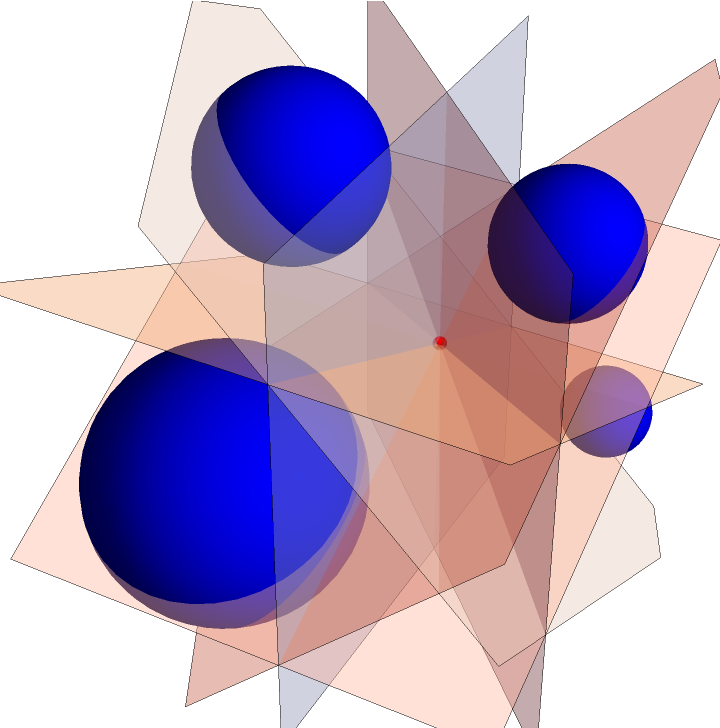 |
This work is licensed under a Creative Commons Attribution 4.0 International License