Basic Examples (2)
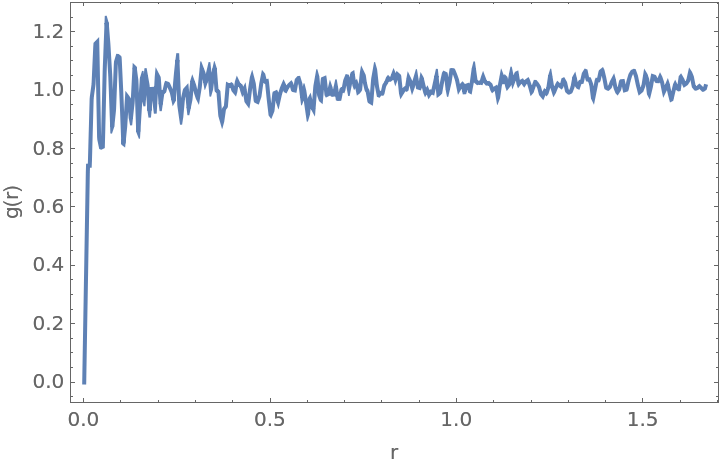
Define random points within a ball and visualize them:
Compute the RDF for the points:
Plot it:
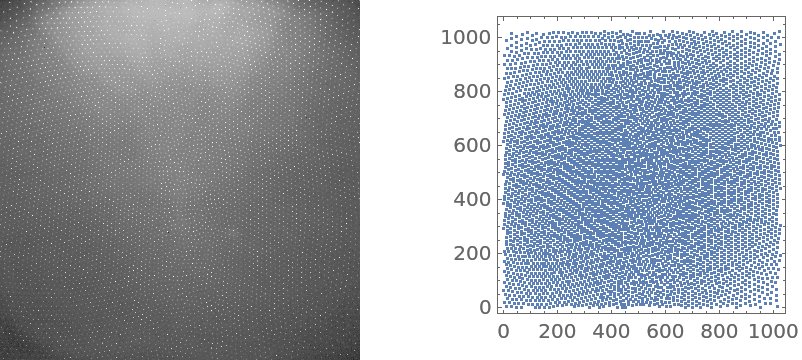
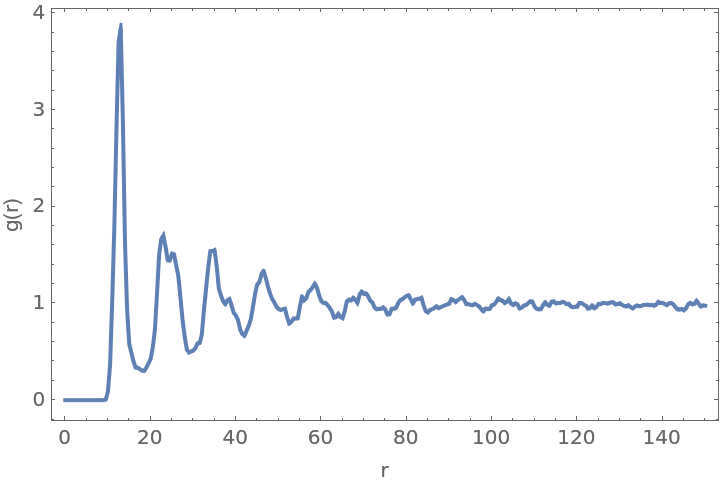
Detect the points in a crystal diffraction image:
Compute the radial distribution function:
Plot the radial distribution function:
Scope (2)
Detect the points in a crystal diffraction image:
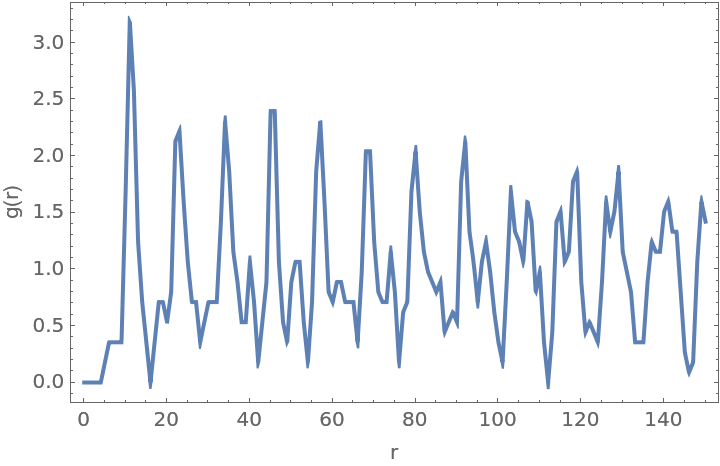
Generate pseudo 1-dimensional data from the image by extracting a narrow slice:
Define a 1-dimensional cuboid region:
Compute the radial distribution function:
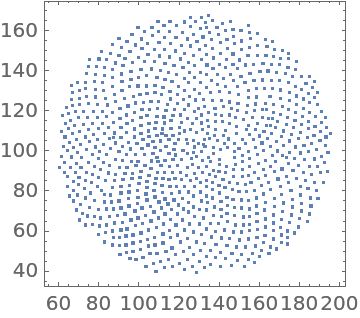
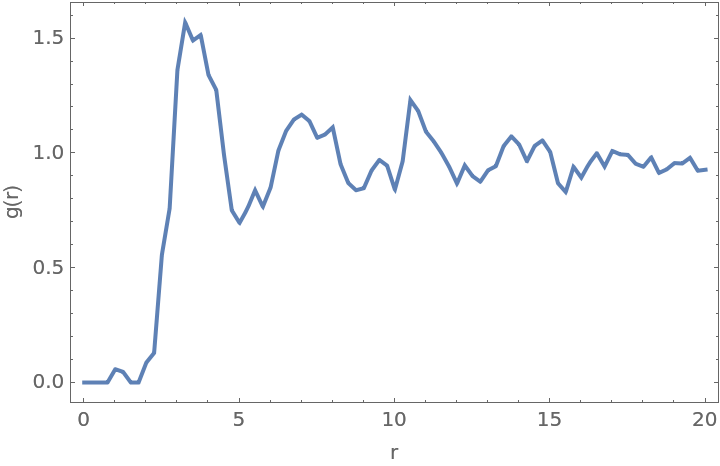
Use a circular region to generate the radial distribution function for sunflower seeds:
Use a mask to remove the petals:
Detect the points representing the seeds:
Define the region (essentially the mask):
Compute the radial distribution function:
The integral of the first peak gives the approximate number of nearest nearest neighbors for a seed:
Applications (8)
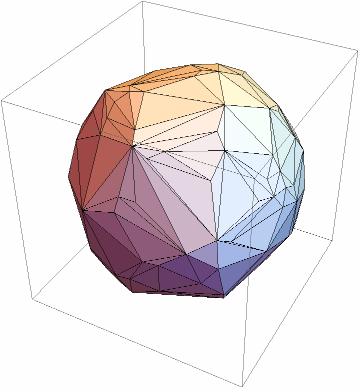
Here is a ball of 1118 water molecules approximately 40 Å in diameter:
Extract the coordinates of the oxygen atoms:
Compute the region by first finding the convex hull of the oxygen atoms:
Then find its centroid, find the distance of the hull point furthest from the centroid, and pad for the approximate diameter of a water molecule of 1.93 Å:
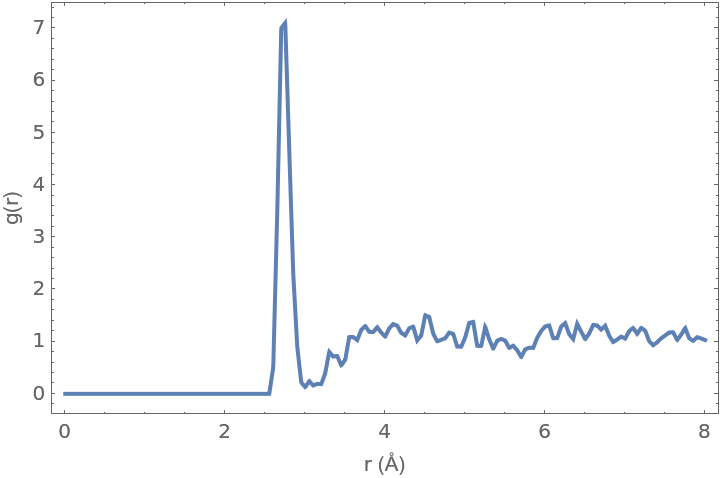
Compute the radial distribution function:
Plot it:
The approximate number of nearest oxygen atoms (water molecules) is:
The average distance is:
Neat Examples (2)
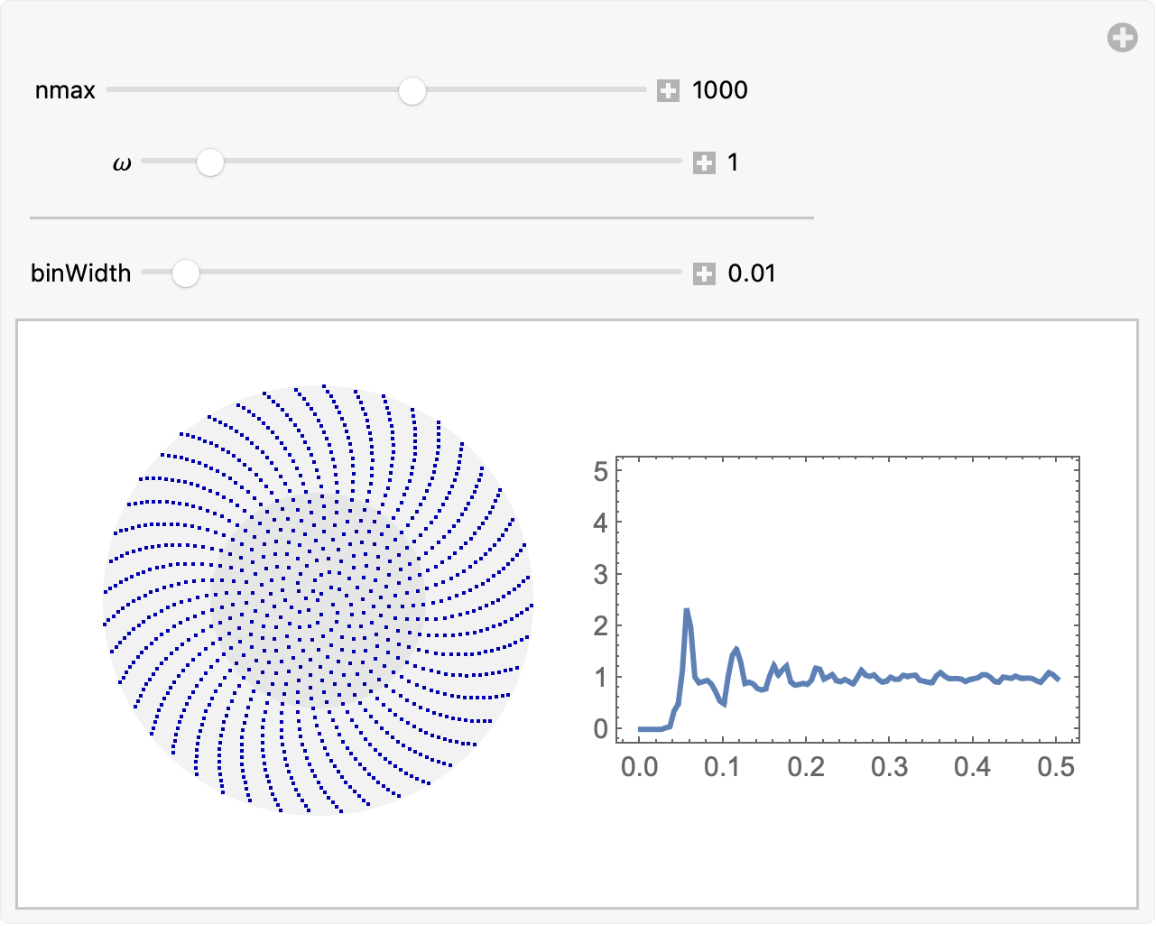
Interactive explorer:
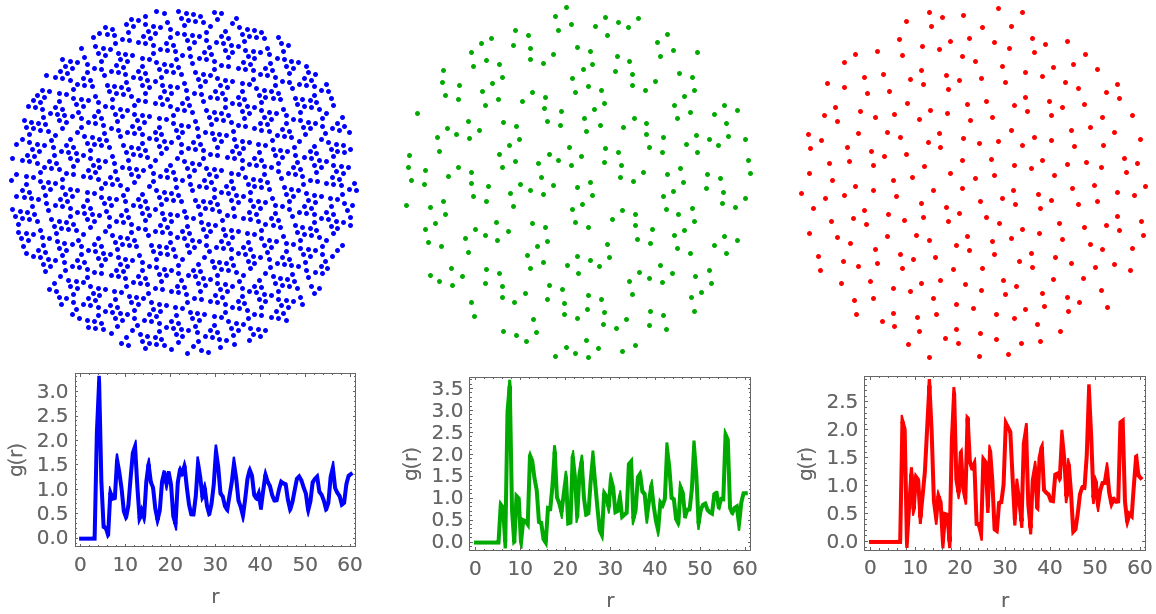
Generate a large patch of the Hat tiling:
Compute the mean of the coordinates of each polygon, and then group by color:
Select the points within the inscribed circle of the hexagonal patch:
Compute the radial distribution function for each group of points and plot it along with the points:

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a5bec337-8e98-400a-81b7-0e0f5ffd30f7"]](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/7d4b824ded706d8e.png)



![seedPoints = Values@ComponentMeasurements[
Binarize@
ImageSubtract[maskedImage, BilateralFilter[image, 4, 1]], "Centroid"] // Select[Last[#] > 36 &] // Echo[#, "", Length] &;
ListPlot[seedPoints, AspectRatio -> Automatic, PlotRange -> MinMax /@ Transpose@seedPoints, PlotRangePadding -> Scaled[.05], ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/75c9ed10b7d3ce79.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/c9da9cf5-0e85-446a-8381-3712127af66b"]](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/0543f9aee2442efc.png)

![oxygenAtoms = Thread[{waterBall["AtomList"], waterBall["AtomCoordinates"]}] // Cases[#, {Atom["O"], xyz_} :> QuantityMagnitude@xyz] &;
oxygenAtoms // Short](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/72c6d3da045ed9db.png)
![DynamicModule[{nmax = 3},
Manipulate[
Module[{M = Floor[10^nmax], pts, \[ScriptR]\[ScriptD]\[ScriptF]}, pts = Table[
Sqrt[k/M] {Cos[\[Omega] k], Sin[\[Omega] k]}, {k, 0., M}];
\[ScriptR]\[ScriptD]\[ScriptF] = ResourceFunction["RadialDistributionFunction"][pts, Ball[{0, 0}, 1], binWidth];
GraphicsRow[{Graphics[{GrayLevel[0.95], Disk[], GrayLevel[0.9], Disk[{0, 0}, 1/2], Darker[Blue], AbsolutePointSize[1], Point[pts]}, ImageSize -> Small], Plot[\[ScriptR]\[ScriptD]\[ScriptF][r], {r, 0, 1/2}, PlotRange -> {0, 5}, PlotRangePadding -> Scaled[.05], Axes -> False, Frame -> True, ImageSize -> Small(*,AspectRatio->
4/5*)]}]], Row[{Control[{{nmax, 3}, 1, 4.5}], " ", Dynamic[Floor[10^nmax]]}], {{\[Omega], 1}, 0, 10, Appearance -> "Labeled"}, Delimiter, {{binWidth, 0.01}, 0.005, 0.1, Appearance -> "Labeled"}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/1ea206bd69afc3fc.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/beaafd39-1767-406e-982b-5c5420463be7"]](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/218c24547de81592.png)

![points = GroupBy[First@
tiling, (Replace[#[[2]], {LightBlue -> Blue, Green -> Darker@Green}] &) -> (Apply[Mean, #[[3]]] &)] // N;](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/0a4aae2cc4670284.png)
![KeyValueMap[{color, coords} |-> Graphics[{color, AbsolutePointSize[2], Point[coords]}, ImageSize -> Small], points] // Row](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/0285b3b18214f7e9.png)

![KeyValueMap[{color, coords} |-> Column[{Graphics[{{color, AbsolutePointSize[2], Point[coords]}}, ImageSize -> Small], \[ScriptCapitalR]\[ScriptCapitalD]\[ScriptCapitalF] = ResourceFunction["RadialDistributionFunction"][coords, Ball[Mean[coords], 95], 1]; Plot[\[ScriptCapitalR]\[ScriptCapitalD]\[ScriptCapitalF][r], {r, 0, 60}, PlotStyle -> color, ImageSize -> Small, PlotRange -> All, Axes -> False, Frame -> True, FrameLabel -> {"r", "g(r)"}]}], points] // Row[#, Spacer[9]] &](https://www.wolframcloud.com/obj/resourcesystem/images/9cf/9cf598f6-0ec2-4104-a7b2-74745a9249fb/52a072247b155a64.png)