Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the queen's graph
ResourceFunction["QueensGraph"][n] generates a undirected graph with n2 vertices representing chess board positions and edges indicating valid moves between configurations. | |
ResourceFunction["QueensGraph"][{m,n}] generates a undirected graph with m×n vertices representing positions of a rectangular chess board. |
The first few n-queens graphs:
| In[1]:= |
| Out[1]= | 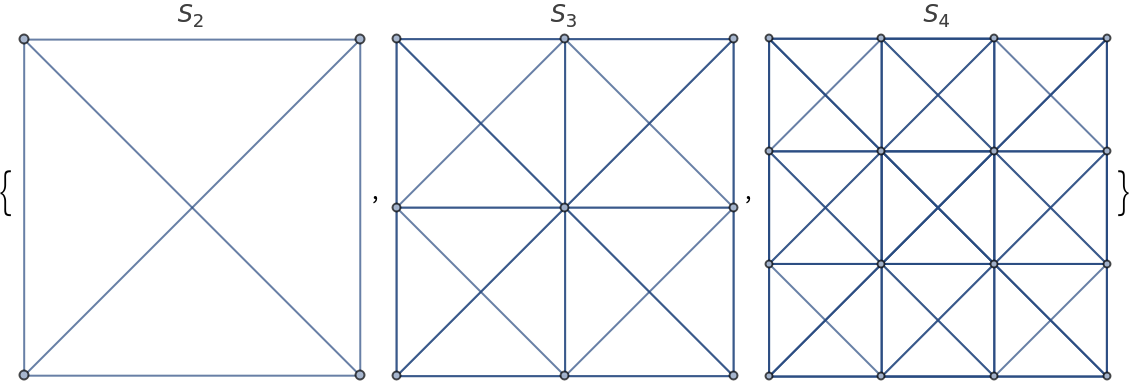 |
Some rectangular queens graphs:
| In[2]:= |
| Out[2]= | 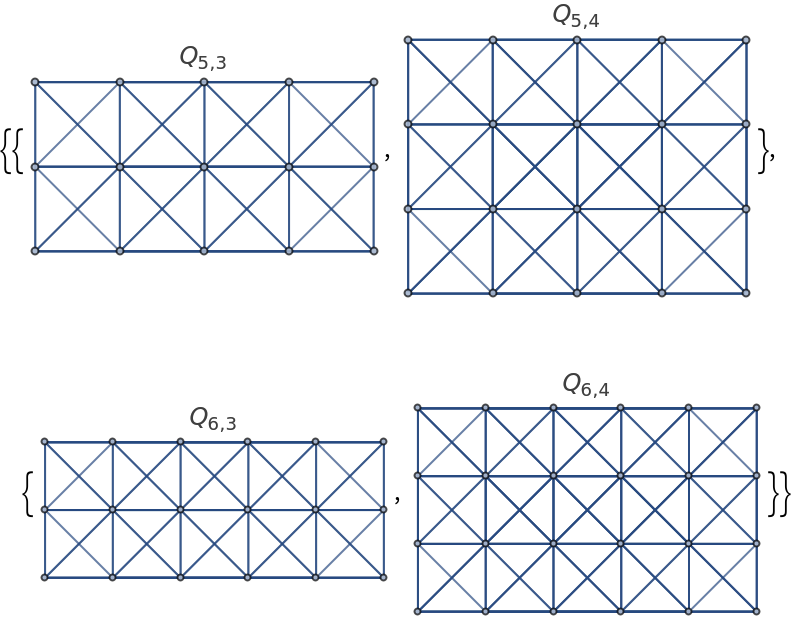 |
The n-Queens graph is automatically laid out in the order of the appearance of the square numbering on the chessboard:
| In[3]:= |
| Out[3]= | 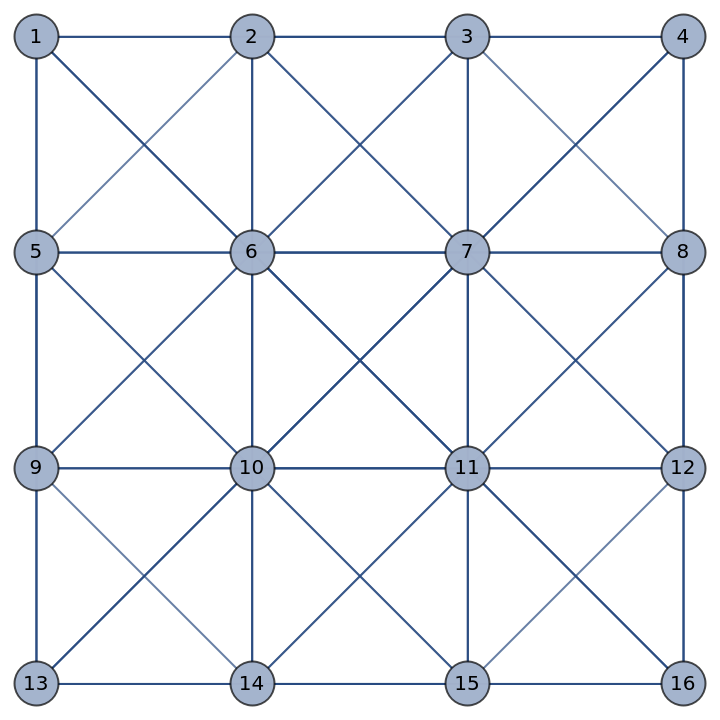 |
Highlight vertex 1:
| In[4]:= |
| Out[4]= | 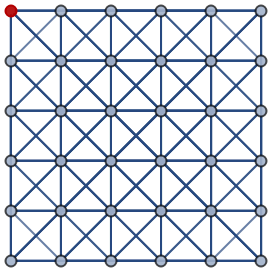 |
Highlight the edge 26:
| In[5]:= |
| Out[5]= | 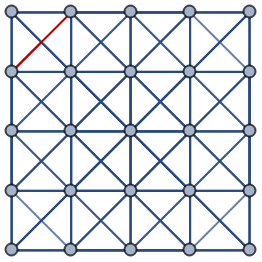 |
Label individual vertices:
| In[6]:= |
| Out[6]= | 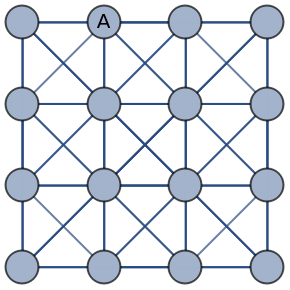 |
Label all vertices:
| In[7]:= |
| Out[7]= | 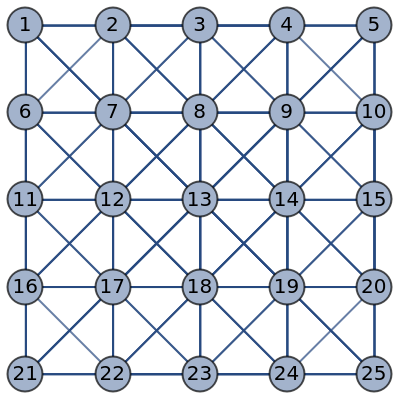 |
By default, the size of vertices is computed automatically:
| In[8]:= |
| Out[8]= |  |
Specify the size of all vertices using symbolic vertex size:
| In[9]:= |
| Out[9]= | 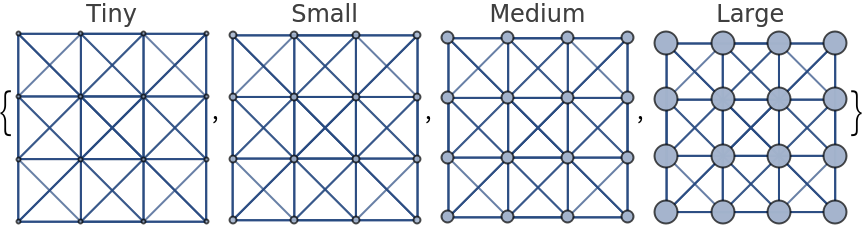 |
Visualize valid moves for the queen:
| In[10]:= | ![HighlightGraph[ResourceFunction["QueensGraph"][{12, 10}], AdjacencyList[ResourceFunction["QueensGraph"][{12, 10}], 53], VertexStyle -> {53 -> Blue}, VertexSize -> {53 -> Medium}, VertexSize -> Medium]](https://www.wolframcloud.com/obj/resourcesystem/images/afe/afe5833c-03e6-48b4-9fda-5336427dace2/5164c56896a79918.png) |
| Out[10]= |  |
The vertex coloring of the queen's graph:
| In[11]:= |
| In[12]:= |
| Out[12]= | 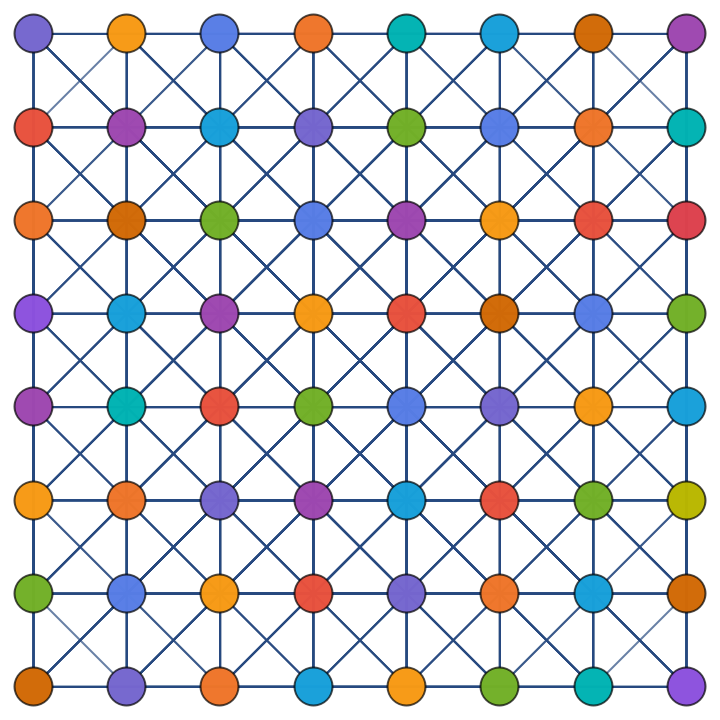 |
This work is licensed under a Creative Commons Attribution 4.0 International License