Function Repository Resource:

QuantumTensorAutomaton

A quantum cellular automaton model that evolves the tensor product of a collection of initial qubits using arbitrary compositions of unitary operators for a finite number of steps

Contributed by: Ruhi Shah and Jonathan Gorard

ResourceFunction["QuantumTensorAutomaton"][matrices,initial,t]

evolves initial for t steps using a composition of unitary matrices given by matrices.

Details and Options

Any number of unitary matrices can be composed. The argument matrices must be a list.

Use "ColourPlot"→True to visualize the state vectors of the individual steps.

Setting "Norms"→True shows the norm-squared probability of being in a given state.

WIth "PlotNorms"→True, ResourceFunction["QuantumTensorAutomaton"] shows the plot of norm-squared probabilities over time.

Common operators to use in the first argument include:

Hadamard:

Rotation:

CNOT:

Pauli (X/Y/Z):

Square root of NOT:

Fourier:

Any unitary operator

Examples

Basic Examples (5)

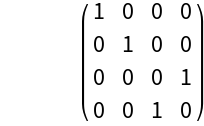
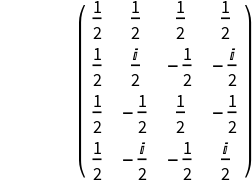
Define a "CNOT" operator:

In[1]:=

$CNOTOperator = SparseArray[{i_, j_} :> If[(IntegerDigits[j - 1, 2, 2] == {IntegerDigits[i - 1, 2, 2][[1]], Mod[-Total@IntegerDigits[i - 1, 2, 2], 2]}), 1, 0], {4, 4}];$

Apply the operator "CNOT" 10 times to an initial state:

In[2]:=

Out[2]=

Visualize the state vectors for the preceding:

In[3]:=

Out[3]=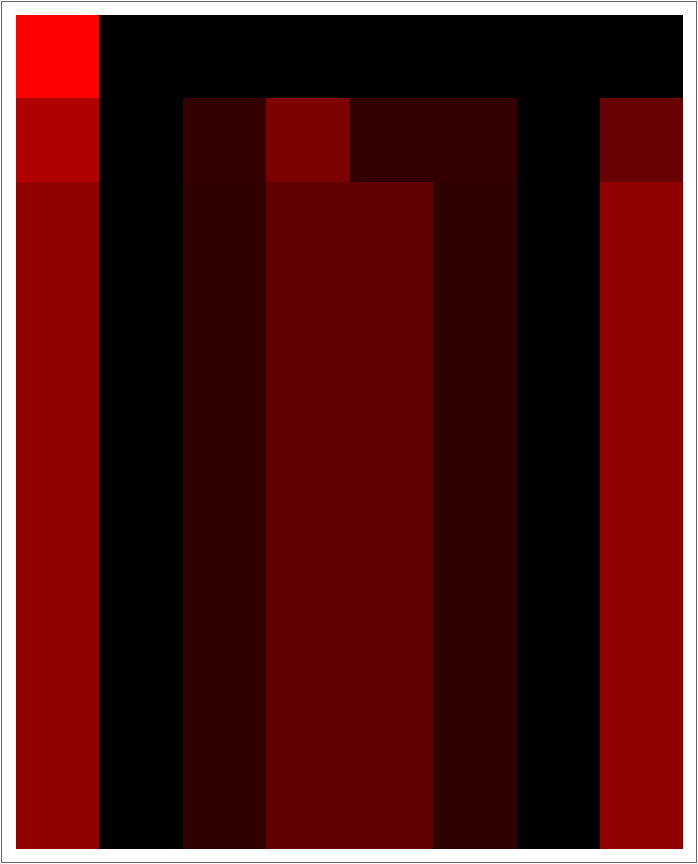

Compute the probabilities (norms squared) for the preceding:

In[4]:=

Out[4]=

Plot the probabilities (norms squared) against the steps (time) for the preceding:

In[5]:=

Out[5]=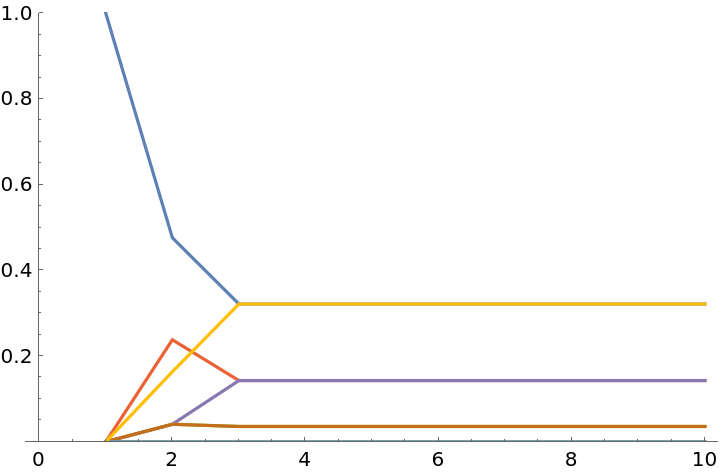

Scope (2)

Define and compose multiple operators:

In[6]:=

$rootNOTOperator = MatrixPower[SparseArray[{{1, 2} -> 1, {2, 1} -> 1}], 1/2]; fourierOperator = SparseArray[({i_, j_} :> Exp[2*Pi*I*Mod[(i - 1)*(j - 1), 4]/4]/Sqrt[4]), {4, 4}]; ResourceFunction[ "QuantumTensorAutomaton"][{rootNOTOperator, fourierOperator}, initialState[3], 10, "ColourPlot" -> True]$

Out[6]=

Random unitary operators will also work:

In[7]:=

randomUnitaryOperator := Module[{randomReal, randomComplex},
randomReal := RandomReal[NormalDistribution[0, 1]];
randomComplex := randomReal + I*randomReal;
Orthogonalize[Table[randomComplex, 4, 4]]];
ResourceFunction["QuantumTensorAutomaton"][{randomUnitaryOperator}, initialState[4], 20, "ColourPlot" -> True]

Out[7]=

Neat Examples (3)

Resonance (3)

Some operators have unique resonance properties:

In[8]:=

resonantOperator = {{0.31074501689103284` + 0.30515668052168954` I, -0.07825046238247854` - 0.6548259330380204` I, 0.15586502550525036` - 0.23792222401422997` I, 0.5402029587275345` - 0.051736543125505546` I}, {-0.11992064793945865` + 0.7226460864976891` I, 0.14410467581259984` + 0.2607778162281067` I, 0.026795182600806336` - 0.0963989236419738` I, -0.10931330562716984` - 0.5938605154095694` I}, {-0.3018042479982458` - 0.11180781815111812` I, 0.2640232260964225` - 0.5326849405682591` I, -0.6175994303955813` + 0.2516898989211491` I, -0.10975792501914561` - 0.2934757811396617` I}, {0.10068802267951421` - 0.3999921704947729` I, 0.336505065324723` - 0.09803808807953789` I, 0.60870542737127` + 0.30625025044774` I, 0.010015864843047728` - 0.4925537830218997` I}}; ResourceFunction[
"QuantumTensorAutomaton"][{resonantOperator}, initialState[4], 400, "NormsPlot" -> True]

Out[8]=

This can be visualized in Fourier space:

In[9]:=

$ListLinePlot[ Map[Norm[#]^2 &, Fourier[#] & /@ Transpose[ ResourceFunction["QuantumTensorAutomaton"][{resonantOperator}, initialState[4], 400, "Norms" -> True]], {2}]]$

Out[9]=

PlotRange→ All reveals the main frequencies:

In[10]:=

$ListLinePlot[ Map[Norm[#]^2 &, Fourier[#] & /@ Transpose[ ResourceFunction["QuantumTensorAutomaton"][{resonantOperator}, initialState[4], 500, "Norms" -> True]], {2}], PlotRange -> All]$